TEMAS DE GEOMETRÍA

"Orthocenter" y "Orthocentre" redirigen aquí. Para el sistema ortocéntrico , vea Sistema ortocéntrico .

Las tres altitudes de un triángulo se intersecan en el ortocentro, que para un triángulo agudo está dentro del triángulo.

En geometría , una altitud de un triángulo es un segmento de línea através de un vértice y perpendicular (es decir, formando un ángulo rectocon) una línea que contiene la base (el lado opuesto al vértice). Esta línea que contiene el lado opuesto se llama la base extendida de la altitud. La intersección de la base extendida y la altitud se llama pie.de la altitud. La longitud de la altitud, a menudo llamada simplemente "la altitud", es la distancia entre la base extendida y el vértice. El proceso de dibujar la altitud desde el vértice al pie se conoce como bajar la altitud en ese vértice. Es un caso especial de proyección ortogonal .

Las altitudes se pueden usar en el cálculo del área de un triángulo: la mitad del producto de la longitud de una altitud y la longitud de su base es igual al área del triángulo. Por lo tanto, la altitud más larga es perpendicular al lado más corto del triángulo. Las altitudes también están relacionadas con los lados del triángulo a través de las funciones trigonométricas .

En un triángulo rectángulo, la altitud de cada ángulo agudo coincide con una pierna y cruza el lado opuesto en (tiene su pie en) el vértice en ángulo recto, que es el ortocentro.

En un triángulo isósceles (un triángulo con dos lados congruentes ), la altitud que tiene el lado incongruente como su base tendrá el punto medio de ese lado como su pie. También la altitud que tiene el lado incongruente como su base será el ángulo bisectriz del ángulo del vértice.

Es común marcar la altitud con la letra h (como en altura ), a menudo con el nombre del lado del que se dibuja la altitud.

En un triángulo rectángulo , la altitud dibujado a la hipotenusa c divide la hipotenusa en dos segmentos de longitudes p y q . Si denotamos la longitud de la altitud por h _c , entonces tenemos la relación

$${\ displaystyle h_ {c} = {\ sqrt {pq}}}  ( Teorema de la media geométrica )

Las altitudes de cada uno de los ángulos agudos de un triángulo obtuso se encuentran totalmente fuera del triángulo, al igual que el ortocentro H.

Para los triángulos agudos y rectos, los pies de las altitudes caen sobre los lados del triángulo (no extendidos). En un triángulo obtuso (uno con un ángulo obtuso ), el pie de la altitud al vértice de ángulo obtuso cae en el interior del lado opuesto, pero los pies de las altitudes a los vértices de ángulo agudo caen en el lado extendido opuesto , exterior al triángulo. Esto se ilustra en el diagrama adyacente: en este triángulo obtuso, una altitud caída perpendicularmente desde el vértice superior, que tiene un ángulo agudo, intersecta el lado horizontal extendido fuera del triángulo.

Ortocentro [ editar ]

Ver también: sistema ortocéntrico.

Tres altitudes que se cruzan en el ortocentro.

Los tres altitudes (posiblemente extendidas) se cruzan en un punto único, llamado el ortocentro del triángulo, generalmente denotado por H. ^[1] [2] El ortocentro se encuentra dentro del triángulo si y solo si el triángulo es agudo (es decir, no tiene un ángulo mayor o igual que un ángulo recto). Si un ángulo es un ángulo recto, el ortocentro coincide con el vértice en el ángulo correcto. ^[2]

Dejemos que A , B , C denoten los vértices y también los ángulos del triángulo, y que a = | BC |, b = | CA |, c = | AB | ser las longitudes de los lados. El ortocentro tiene coordenadas trilineales ^[3]

$${\ displaystyle \ sec A: \ sec B: \ sec C = \ cos A- \ sin B \ sin C: \ cos B- \ sin C \ sin A: \ cos C- \ sin A \ sin B,}

y coordenadas baricéntricas

$${\ displaystyle \ displaystyle (a ^ {2} + b ^ {2} -c ^ {2}) (a ^ {2} -b ^ {2} + c ^ {2}) :( a ^ {2} + b ^ {2} -c ^ {2}) (- a ^ {2} + b ^ {2} + c ^ {2}) :( a ^ {2} -b ^ {2} + c ^ { 2}) (- a ^ {2} + b ^ {2} + c ^ {2})}

$${\ displaystyle = \ tan A: \ tan B: \ tan C.}

Como las coordenadas baricéntricas son todas positivas para un punto en el interior de un triángulo, pero al menos uno es negativo para un punto en el exterior, y dos de las coordenadas baricéntricas son cero para un punto de vértice, las coordenadas baricéntricas dadas para el ortocentro muestran que el ortocentro está en elinterior de un triángulo agudo , en el vértice en ángulo recto de un triángulo rectángulo , y en el exterior a un triángulo obtuso .

En el plano complejo , los puntos A , B y C representan los números $${\ displaystyle z_ {A}}, $${\ displaystyle z_ {B}} y, respectivamente, $${\ displaystyle z_ {C}}y suponga que el circuncentro del triángulo ABC está ubicado en el origen del plano. Entonces, el número complejo

$${\ displaystyle z_ {H} = z_ {A} + z_ {B} + z_ {C}}

Está representado por el punto H , es decir, el ortocentro del triángulo ABC . ^[4] A partir de esto, se pueden establecer directamente las siguientes caracterizaciones del ortocentro H mediante vectores libres :

$${\ displaystyle {\ vec {OH}} = \ sum \ limits _ {\ scriptstyle {\ rm {cyclic}}} {\ vec {OA}}, \ qquad 2 \ cdot {\ vec {HO}} = \ sum \ limits _ {\ scriptstyle {\ rm {cyclic}}} {\ vec {HA}}.}

La primera de las identidades vectoriales anteriores también se conoce como el problema de Sylvester , propuesto por James Joseph Sylvester . ^[5]

Propiedades [ editar ]

Sean D , E y F los pies de las altitudes desde A , B y C respectivamente. Entonces:

• El producto de las longitudes de los segmentos en los que el ortocentro divide una altitud es el mismo para las tres altitudes: ^[6] [7]

$${\ displaystyle AH \ cdot HD = BH \ cdot HE = CH \ cdot HF.}

El círculo centrado en H que tiene el radio de la raíz cuadrada de esta constante es el círculo polar del triángulo . ^[8]

• La suma de las relaciones en las tres altitudes de la distancia del ortocentro desde la base hasta la longitud de la altitud es 1: ^[9] (Esta propiedad y la siguiente son aplicaciones de una propiedad más general de cualquier punto interior y la Tres cevianos a través de él.

$${\ displaystyle {\ frac {HD} {AD}} + {\ frac {HE} {BE}} + {\ frac {HF} {CF}} = 1.}

• La suma de las relaciones en las tres altitudes de la distancia del ortocentro desde el vértice hasta la longitud de la altitud es 2: ^[9]

$${\ displaystyle {\ frac {AH} {AD}} + {\ frac {BH} {BE}} + {\ frac {CH} {CF}} = 2.}

• El conjugado isogonal del ortocentro es el circuncentro del triángulo. ^[10]

• El conjugado isotómico del ortocentro es el punto simmedio del triángulo anticomplementario . ^[11]

• Cuatro puntos en el plano, de modo que uno de ellos es el ortocentro del triángulo formado por los otros tres, se denomina sistema ortocéntrico o cuadrángulo ortocéntrico.

Relación con los círculos y las cónicas [ editar ]

Denotan la circunferencia circunscrita del triángulo por R . Entonces ^[12] [13]

$${\ displaystyle a ^ {2} + b ^ {2} + c ^ {2} + AH ^ {2} + BH ^ {2} + CH ^ {2} = 12R ^ {2}.}

Además, denotando r como el radio del incircle del triángulo , r _a , r _b , y r _c como el radio de sus excírculos , y Rnuevamente como el radio de su circuncírculo, las siguientes relaciones se mantienen con respecto a las distancias del ortocentro desde Los vértices: ^[14]

$${\ displaystyle r_ {a} + r_ {b} + r_ {c} + r = AH + BH + CH + 2R,}

$${\ displaystyle r_ {a} ^ {2} + r_ {b} ^ {2} + r_ {c} ^ {2} + r ^ {2} = AH ^ {2} + BH ^ {2} + CH ^ {2} + (2R) ^ {2}.}

Si cualquier altitud, por ejemplo, AD , se extiende para intersectar la circunferencia circunscrita en P , de manera que AP es una cuerda de la circunferencia circunscrita, luego el pie D biseca segmento HP : ^[7]

$${\ displaystyle HD = DP.}

Las directrices de todas las parábolas que son externamente tangentes a un lado de un triángulo y tangentes a las extensiones de los otros lados pasan a través del ortocentro. ^[15]

Una circunferencia que pasa a través del ortocentro de un triángulo es una hipérbola rectangular . ^[dieciséis]

Relación con otros centros, el círculo de nueve puntos [ editar ]

Artículo principal: Círculo de nueve puntos.

El ortocentro H , el centroide G , el circuncentro O y el centro N del círculo de nueve puntos se encuentran en una sola línea, conocida como la línea de Euler . ^[17] El centro del círculo de nueve puntos se encuentra en el punto medio de la línea de Euler, entre el ortocentro y el circuncentro, y la distancia entre el centroide y el circuncentro es la mitad que entre el centroide y el ortocentro: ^[18]

$${\ displaystyle OH = 2NH,}

$${\ displaystyle 2OG = GH.}

El ortocentro está más cerca del incentivo I que del centroide, y el ortocentro está más lejos que el incentivo del centroide:

{\ displaystyle HI

{\ displaystyle HG> IG.}

En términos de los lados a, b, c , inradius r y circumradius R , ^[19]

$${\ displaystyle OH ^ {2} = R ^ {2} -8R ^ {2} \ cos A \ cos B \ cos C = 9R ^ {2} - (a ^ {2} + b ^ {2} + c ^ {2}),}^{[20] : p. 449}

$${\ displaystyle HI ^ {2} = 2r ^ {2} -4R ^ {2} \ cos A \ cos B \ cos C.}

Triángulo ortico [ editar ]

El triángulo abc (respectivamente, DEF en el texto) es el triángulo órtico del triángulo ABC

Si el triángulo ABC es oblicuo (no contiene un ángulo recto), el triángulo del pedal del ortocentro del triángulo original se llama triángulo órtico o triángulo de altitud . Es decir, los pies de las altitudes de un triángulo oblicuo forman el triángulo órtico, DEF . Además, el incentivo (el centro del círculo inscrito) del triángulo ortéptico DEF es el ortocentro del triángulo original ABC . ^[21]

Las coordenadas trilineales para los vértices del triángulo órtico están dadas por

• D = 0: sec B  : sec C
• E = sec A  : 0: sec C
• F = sec A  : sec B  : 0 .

Los lados extendidos del triángulo órtico se encuentran con los lados extendidos opuestos de su triángulo de referencia en tres puntos colineales . ^{[22] [23] [21]}

En cualquier triángulo agudo , el triángulo inscrito con el perímetro más pequeño es el triángulo órtico. ^[24] Esta es la solución al problema de Fagnano , planteada en 1775. ^[25] Los lados del triángulo órtico son paralelos a las tangentes del circuncírculo en los vértices del triángulo original. ^[26]

El triángulo órtico de un triángulo agudo da una ruta de luz triangular. ^[27]

Las líneas tangentes del círculo de nueve puntos en los puntos medios de los lados de ABC son paralelas a los lados del triángulo órtico, formando un triángulo similar al triángulo órtico. ^[28]

El triángulo órtico está estrechamente relacionado con el triángulo tangencial , construido de la siguiente manera: sea L _A la línea tangente al circuncírculo del triángulo ABC en el vértice A , y defina L _B y L _{C de manera} análoga. Sea A " = L _B  ∩  L _C , B" = L _C  ∩  L _A , C " = L _C  ∩  L _A. El triángulo tangencial es A" B "C", cuyos lados son las tangentes al triángulo circuncírico de ABC en sus vértices; Es homotética al triángulo órtico. El circuncentro del triángulo tangencial y el centro de similitud de los triángulos órtico y tangencial están en la línea de Euler . ^{[20] : p. 447}

Las coordenadas trilineales para los vértices del triángulo tangencial están dadas por

• A " = - a  : b  : c
• B " = a  : - b  : c
• C " = a  : b  : - c .

Para más información sobre el triángulo órtico, vea aquí .

Algunos teoremas de altitud adicionales [ editar ]

Altitud en términos de los lados [ editar ]

Para cualquier triángulo con lados a, b, c y semiperímetro s = ( a + b + c ) / 2 , la altitud del lado a viene dada por

$${\ displaystyle h_ {a} = {\ frac {2 {\ sqrt {s (sa) (sb) (sc)}}} {a}}.}

Esto se deduce de la combinación de la fórmula de Heron para el área de un triángulo en términos de los lados con la fórmula del área (1/2) × × base de altura, donde la base se toma como lado una y la altura es la altura de A .

Teoremas inradio [ editar ]

Considere un triángulo arbitrario con lados a, b, c y con las altitudes correspondientes h _a , h _b y h _c . Las altitudes y el radio del incírculo r están relacionados por ^{[29] : Lemma 1}

$${\ displaystyle \ displaystyle {\ frac {1} {r}} = {\ frac {1} {h_ {a}}} + {\ frac {1} {h_ {b}}} + {\ frac {1} {h_ {c}}}.}

Circunradio teorema [ editar ]

Denotando la altitud desde un lado de un triángulo como h _a , los otros dos lados como b y c , y la circunferenciadel triángulo (radio del círculo circunscrito del triángulo) como R , la altitud viene dada por ^[30]

$${\ displaystyle h_ {a} = {\ frac {bc} {2R}}.

Punto interior [ editar ]

Si p ₁ , p ₂ y p ₃ son las distancias perpendiculares desde cualquier punto P a los lados, y h ₁ , h ₂ y h ₃ son las altitudes a los lados respectivos, entonces ^[31]

$${\ displaystyle {\ frac {p_ {1}} {h_ {1}}} + {\ frac {p_ {2}} {h_ {2}}} + {\ frac {p_ {3}} {h_ {3 }}} = 1.}

Teorema del área [ editar ]

Denotando las altitudes de cualquier triángulo desde los lados a , b y c respectivamente como$${\ displaystyle h_ {a}}, $${\ displaystyle h_ {b}}y $${\ displaystyle h_ {c}}, y denotando la semi-suma de los recíprocos de las altitudes como $${\ displaystyle H = (h_ {a} ^ {- 1} + h_ {b} ^ {- 1} + h_ {c} ^ {- 1}) / 2}nosotros tenemos ^[32]

$${\ displaystyle \ mathrm {Área} ^ {- 1} = 4 {\ sqrt {H (H-h_ {a} ^ {- 1}) (H-h_ {b} ^ {- 1}) (H-h_ {c} ^ {- 1})}}.}

Punto general sobre una altitud [ editar ]

Si E es cualquier punto en una altitud AD de cualquier triángulo ABC , entonces ^{[33] : 77–78}

$${\ displaystyle AC ^ {2} + EB ^ {2} = AB ^ {2} + CE ^ {2}.}

Triángulos de casos especiales [ editar ]

Triángulo equilátero [ editar ]

Para cualquier punto P dentro de un triángulo equilátero , la suma de las perpendiculares a los tres lados es igual a la altitud del triángulo. Este es el teorema de Viviani .

Triángulo rectángulo [ editar ]

La altitud de un triángulo rectángulo desde su ángulo recto hasta su hipotenusa es la media geométrica de las longitudes de los segmentos en que se divide la hipotenusa. Usando el teorema de Pitágoras en los 3 triángulos de lados ( p  +  q , r , s ) , ( r , h , p ) y ( s , h , q ) ,
{\ displaystyle {\ begin {alineado} (p + q) ^ {2} \ quad & = \ quad \; \, r ^ {2} \ quad + \ quad s ^ {2} \\ p ^ {2} \! + 2pq + q ^ {2} & = \ left (h ^ {2} \! \! + \! P ^ {2} \ right) \! + \! \ Left (h ^ {2} \! \! + \! q ^ {2} \ right) \\ 2pq \ qquad \, & = 2h ^ {2} \ quad \ por lo tanto h = {\ sqrt {pq}} \\\ end {alineado}}}

En un triángulo rectángulo, las tres altitudes h _a , h _b y h _c (las dos primeras de las cuales son iguales a las longitudes de las piernas b y arespectivamente) se relacionan según ^[34] [35]

$${\ displaystyle {\ frac {1} {h_ {a} ^ {2}}} + {\ frac {1} {h_ {b} ^ {2}}} = {\ frac {1} {h_ {c} ^ {2}}}.}

la fórmula de Brahmagupta se usa para encontrar el área de cualquier cuadrilátero cíclico (uno que se puede inscribir en un círculo) dadas las longitudes de los lados.

Fórmula [ editar ]

La fórmula de Brahmagupta da el área K de un cuadrilátero cíclico cuyos lados tienen longitudes a , b , c , dcomo

$${\ displaystyle K = {\ sqrt {(sa) (sb) (sc) (sd)}}}

donde s , el semiperímetro , se define como

$${\ displaystyle s = {\ frac {a + b + c + d} {2}}.}

Esta fórmula generaliza la fórmula de Heron para el área de un triángulo . Un triángulo puede considerarse como un cuadrilátero con un lado de longitud cero. Desde esta perspectiva, cuando d se acerca a cero, un cuadrilátero cíclico converge en un triángulo cíclico (todos los triángulos son cíclicos), y la fórmula de Brahmagupta se simplifica a la fórmula de Heron.

Si el semiperímetro no se usa, la fórmula de Brahmagupta es

$${\ displaystyle K = {\ frac {1} {4}} {\ sqrt {(-a + b + c + d) (a-b + c + d) (a + b-c + d) (a + b + cd)}}.}

Otra versión equivalente es

$${\ displaystyle K = {\ frac {\ sqrt {(a ^ {2} + b ^ {2} + c ^ {2} + d ^ {2}) ^ {2} + 8abcd-2 (a ^ {4 } + b ^ {4} + c ^ {4} + d ^ {4})}} {4}} \ cdot}

Prueba [ editar ]

Diagrama de referencia

Prueba trigonométrica [ editar ]

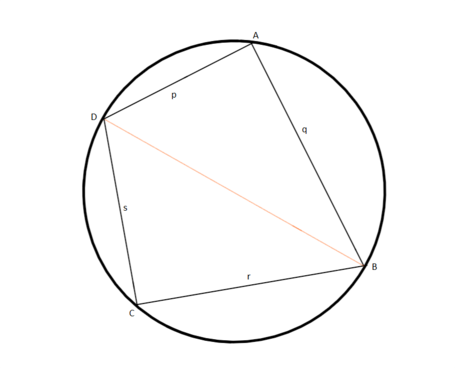
Aquí se utilizan las anotaciones en la figura de la derecha. El área Kdel cuadrilátero cíclico es igual a la suma de las áreas de △ ADB y △ BDC :

$${\ displaystyle = {\ frac {1} {2}} pq \ sin A + {\ frac {1} {2}} rs \ sin C.}

Pero como ABCD es un cuadrilátero cíclico, ∠ DAB = 180 ° - ∠ DCB . Por lo tanto pecado A = sen C . Por lo tanto,

$${\ displaystyle K = {\ frac {1} {2}} pq \ sin A + {\ frac {1} {2}} rs \ sin A}

$${\ displaystyle K ^ {2} = {\ frac {1} {4}} (pq + rs) ^ {2} \ sin ^ {2} A}

$${\ displaystyle 4K ^ {2} = (pq + rs) ^ {2} (1- \ cos ^ {2} A) = (pq + rs) ^ {2} - (pq + rs) ^ {2} \ cos ^ {2} A.}

Resolviendo para el lado común DB , en △ ADB y △ BDC , la ley de cosenos da

$${\ displaystyle p ^ {2} + q ^ {2} -2pq \ cos A = r ^ {2} + s ^ {2} -2rs \ cos C.}

Sustituyendo cos C = −cos A (ya que los ángulos A y C son suplementarios ) y reorganizando, tenemos

$${\ displaystyle 2 (pq + rs) \ cos A = p ^ {2} + q ^ {2} -r ^ {2} -s ^ {2}.}

Sustituyendo esto en la ecuación para el área,

$${\ displaystyle 4K ^ {2} = (pq + rs) ^ {2} - {\ frac {1} {4}} (p ^ {2} + q ^ {2} -r ^ {2} -s ^ {2}) ^ {2}}

$${\ displaystyle 16K ^ {2} = 4 (pq + rs) ^ {2} - (p ^ {2} + q ^ {2} -r ^ {2} -s ^ {2}) ^ {2}. }

El lado derecho tiene la forma a ² - b ² = ( a - b ) ( a + b ) y, por lo tanto, puede escribirse como

$${\ displaystyle [2 (pq + rs) -p ^ {2} -q ^ {2} + r ^ {2} + s ^ {2}] [2 (pq + rs) + p ^ {2} + q ^ {2} -r ^ {2} -s ^ {2}]}

que, al reordenar los términos entre corchetes, cede

$${\ displaystyle = [(r + s) ^ {2} - (pq) ^ {2}] [(p + q) ^ {2} - (rs) ^ {2}]}

$${\ displaystyle = (q + r + sp) (p + r + sq) (p + q + sr) (p + q + rs).}

Presentamos el semiperímetro S = p + q + r + s/2 ,

$${\ displaystyle 16K ^ {2} = 16 (Sp) (Sq) (Sr) (Ss).}

Tomando la raíz cuadrada, obtenemos

$${\ displaystyle K = {\ sqrt {(Sp) (Sq) (Sr) (Ss)}}.}

No trigonométrica prueba [ editar ]

Una prueba alternativa, no trigonométrica, utiliza dos aplicaciones de la fórmula del área del triángulo de Heron en triángulos similares. ^[1]

Extensión a cuadriláteros no cíclicos [ editar ]

En el caso de cuadriláteros no cíclicos, la fórmula de Brahmagupta puede extenderse considerando las medidas de dos ángulos opuestos del cuadrilátero:

$${\ displaystyle K = {\ sqrt {(sa) (sb) (sc) (sd) -abcd \ cos ^ {2} \ theta}}}

donde θ es la mitad de la suma de dos ángulos opuestos. (La elección de qué par de ángulos opuestos es irrelevante: si se toman los otros dos ángulos, la mitad de su suma es 180 ° - θ . Dado que cos (180 ° - θ ) = −cos θ , tenemos cos ² (180 ° - θ ) = cos ² θ .) Esta fórmula más general se conoce como fórmula de Bretschneider .

Es una propiedad de los cuadriláteros cíclicos (y, en última instancia, de los ángulos inscritos ) que los ángulos opuestos de un cuadrilátero suman 180 °. En consecuencia, en el caso de un cuadrilátero inscrito, θ es 90 °, de donde el término

$${\ displaystyle abcd \ cos ^ {2} \ theta = abcd \ cos ^ {2} \ left (90 ^ {\ circ} \ right) = abcd \ cdot 0 = 0,}

Dando la forma básica de la fórmula de Brahmagupta. De la última ecuación se deduce que el área de un cuadrilátero cíclico es el área máxima posible para cualquier cuadrilátero con las longitudes de los lados dados.

Una fórmula relacionada, que fue probada por Coolidge , también da el área de un cuadrilátero convexo general. Es ^[2]

$${\ displaystyle K = {\ sqrt {(sa) (sb) (sc) (sd) - \ textstyle {1 \ sobre 4} (ac + bd + pq) (ac + bd-pq)}}}

donde p y q son las longitudes de las diagonales del cuadrilátero. En un cuadrilátero cíclico , pq = ac + bd según el teorema de Ptolomeo , y la fórmula de Coolidge se reduce a la fórmula de Brahmagupta.

Teoremas relacionados [ editar ]

• La fórmula de Heron para el área de un triángulo es el caso especial que se obtiene al tomar d = 0 .
• La relación entre la forma general y la forma extendida de la fórmula de Brahmagupta es similar a cómo la ley de los cosenos extiende el teorema de Pitágoras .
• Existen fórmulas de forma cerrada cada vez más complicadas para el área de polígonos generales en círculos, según lo descrito por Maley et al.