En geometría , se dice que tres o más líneas en un plano o espacio de dimensión superior son concurrentessi se intersecan en un solo punto .

Ejemplos [ editar ]
Triángulos [ editar ]
En un triángulo , cuatro tipos básicos de conjuntos de líneas concurrentes son altitudes , bisectrices de ángulos , medianas y bisectrices perpendiculares :
- Las altitudes de un triángulo se extienden desde cada vértice y se encuentran con el lado opuesto en un ángulo recto . El punto donde se encuentran las tres altitudes es el ortocentro .
- Las bisectrices de ángulo son rayos que corren desde cada vértice del triángulo y que dividen en dos el ángulo asociado . Todos se reúnen en el incentivo .
- Las medianas conectan cada vértice de un triángulo al punto medio del lado opuesto. Las tres medianas se encuentran en el centroide .
- Las bisectrices perpendiculares son líneas que se salen de los puntos medios de cada lado de un triángulo en ángulos de 90 grados. Las tres bisectrices perpendiculares se encuentran en el circuncentro .
Otros conjuntos de líneas asociadas con un triángulo también son concurrentes. Por ejemplo:
- Cualquier mediana (que es necesariamente una bisectriz del área del triángulo ) es concurrente con otras dos bisectrices de área, cada una de las cuales es paralela a un lado. [1]
- Una cuchilla de un triángulo es un segmento de línea que divide el perímetro del triángulo y tiene un punto final en el punto medio de uno de los tres lados. Las tres cuchillas coinciden en el centro del círculo de Spieker , que es el incircle del triángulo medial .
- Un divisor de un triángulo es un segmento de línea que tiene un punto final en uno de los tres vértices del triángulo y divide el perímetro en dos. Los tres divisores coinciden en el punto de Nagel del triángulo.
- Cualquier línea a través de un triángulo que divide tanto el área del triángulo y su perímetro en un medio pasa a través del triángulo incentro , y cada triángulo tiene uno, dos, o tres de estas líneas. [2] Por lo tanto, si hay tres de ellos, concurren en el incentivo.
- El punto Tarry de un triángulo es el punto de concurrencia de las líneas a través de los vértices del triángulo perpendicular a los lados correspondientes del primer triángulo de Brocard del triángulo .
- El punto de Schiffler de un triángulo es el punto de concurrencia de las líneas de Euler de cuatro triángulos: el triángulo en cuestión, y los tres triángulos que comparten dos vértices con él y tienen su incentivo como el otro vértice.
- Los puntos de Napoleón y sus generalizaciones son puntos de concurrencia. Por ejemplo, el primer punto de Napoleón es el punto de concurrencia de las tres líneas, cada una desde un vértice hasta el centroide del triángulo equilátero dibujado en el exterior del lado opuesto del vértice. Una generalización de esta noción es el punto jacobi .
- El punto de Longchamps es el punto de concurrencia de varias líneas con la línea de Euler .
- Tres líneas, cada una formada dibujando un triángulo equilátero externo en uno de los lados de un triángulo dado y conectando el nuevo vértice al vértice opuesto del triángulo original, son concurrentes en un punto llamado el primer centro isogonal . En el caso en el que el triángulo original no tenga un ángulo superior a 120 °, este punto también es el punto Fermat .
- El punto Apolonio es el punto de concurrencia de tres líneas, cada uno de los cuales conecta un punto de tangencia del círculo a la que del triángulo excircles son internamente tangente, con el vértice opuesto del triángulo.
Cuadriláteros [ editar ]
- Los dos bimedianos de un cuadrilátero (segmentos que unen puntos medios de lados opuestos) y el segmento de línea que une los puntos medios de las diagonales son concurrentes y todos están biseccionados por su punto de intersección. [3] : p.125
- En un cuadrilátero tangencial , las cuatro bisectrices de ángulo concurren en el centro del incircle . [4]
- Aquí se dan otras concurrencias de un cuadrilátero tangencial .
- En un cuadrilátero cíclico , cuatro segmentos de línea, cada uno perpendicular a un lado y que pasan a través del punto medio del lado opuesto , son concurrentes. [3] : p.131; [5] Estos segmentos de línea se llaman maltitudes , [6] que es una abreviatura para la altura del punto medio. Su punto común se llama el anticentro .
- Un cuadrilátero convexo es ex tangencial si y solo si hay seis bisectrices de ángulos concurrentes: las bisectrices de ángulo interno en dos ángulos de vértice opuestos, las bisectrices de ángulo externo en los otros dos ángulos de vértice, y las bisectrices de ángulo externo en los ángulos formados donde Extensiones de lados opuestos se intersecan.
Hexágonos [ editar ]
- Si los lados sucesivos de un hexágono cíclico son a , b , c , d , e , f , entonces las tres diagonales principales concurren en un solo punto si y solo si ace = bdf . [7]
- Si un hexágono tiene una cónica inscrita , entonces según el teorema de Brianchon, sus diagonalesprincipales son concurrentes (como en la imagen de arriba).
- Las líneas concurrentes surgen en el dual del teorema del hexágono de Pappus .
- Para cada lado de un hexágono cíclico, extienda los lados adyacentes a su intersección, formando un triángulo exterior al lado dado. Entonces los segmentos que conectan los circuncentrantes de triángulos opuestos son concurrentes. [8]
Polígonos regulares [ editar ]
- Si un polígono regular tiene un número par de lados, las diagonales que conectan los vértices opuestos son concurrentes en el centro del polígono.
Círculos [ editar ]
- Las bisectrices perpendiculares de todos los acordes de un círculo son concurrentes en el centro del círculo.
- Las líneas perpendiculares a las tangentes a un círculo en los puntos de tangencia son concurrentes en el centro.
- Todas las bisectrices de área y las bisectrices de perímetro de un círculo son diámetros , y son concurrentes en el centro del círculo.
Elipses [ editar ]
- Todas las bisectrices de área y las bisectrices de perímetro de una elipse son concurrentes en el centro de la elipse.
Hyperbolas [ editar ]
- En una hipérbola, los siguientes son concurrentes: (1) un círculo que pasa a través de los focos de la hipérbola y se centra en el centro de la hipérbola; (2) cualquiera de las líneas que son tangentes a la hipérbola en los vértices; y (3) cualquiera de las asíntotas de la hipérbola.
- Los siguientes también son concurrentes: (1) el círculo que está centrado en el centro de la hipérbola y que pasa a través de los vértices de la hipérbola; (2) ya sea directriz; y (3) cualquiera de las asíntotas.
Tetraedros [ editar ]
- En un tetraedro , las cuatro medianas y las tres bimedianas son concurrentes en un punto llamado centroidedel tetraedro. [9]
- Un tetraedro isodinámico es uno en el que los cevianos que unen los vértices a los incentivos de las caras opuestas son concurrentes, y un tetraedro isogónico tiene cevianos concurrentes que unen los vértices a los puntos de contacto de las caras opuestas con la esfera inscrita del tetraedro. .
- En un tetraedro ortocéntrico las cuatro altitudes son concurrentes.
Álgebra [ editar ]
Según el teorema de Rouché-Capelli , un sistema de ecuaciones es consistente si y solo si el rango de la matriz de coeficientes es igual al rango de la matriz aumentada (la matriz de coeficientes aumentada con una columna de términos de intercepción), y el sistema tiene una solución única si y solo si ese rango común es igual al número de variables. Así, con dos variables, las k líneas en el plano, asociadas con un conjunto de k ecuaciones, son concurrentes si y solo si el rango de la matriz del coeficiente k × 2 y el rango de la matriz aumentada k × 3 son ambos 2. En ese sentido caso solo dos de losLas ecuaciones k son independientes , y el punto de concurrencia se puede encontrar resolviendo cualquiera de las dos ecuaciones mutuamente independientes simultáneamente para las dos variables.
Geometría proyectiva [ editar ]
En geometría proyectiva , en dos dimensiones, la concurrencia es el doble de colinealidad ; en tres dimensiones, la concurrencia es la dualidad de la coplanaridad .
En la geometría plana , un ángulo es la figura formada por dos rayos , llamados lados del ángulo, que comparten un punto final común, llamado el vértice del ángulo. [1] Los ángulos formados por dos rayos se encuentran en un plano, pero este plano no tiene que ser un plano euclidiano . Los ángulos también están formados por la intersección de dos planos en espacios euclidianos y otros . Estos se llaman ángulos diedros . Los ángulos formados por la intersección de dos curvas en un plano se definen como el ángulo determinado por los rayos tangentes en el punto de intersección. Declaraciones similares se mantienen en el espacio, por ejemplo, el ángulo esférico.formado por dos grandes círculos en una esfera es el ángulo diedro entre los planos determinados por los grandes círculos.
El ángulo también se utiliza para designar la medida de un ángulo o de una rotación . Esta medida es la relación entre la longitud de un arco circular y su radio . En el caso de un ángulo geométrico, el arco está centrado en el vértice y delimitado por los lados. En el caso de una rotación, el arco se centra en el centro de la rotación y está delimitado por cualquier otro punto y su imagen por la rotación.
La palabra ángulo proviene de la palabra latina angulo , que significa "esquina"; las palabras cognadas son el griego ἀγκύλος (ankylοs) , que significa "torcido, curvado", y la palabra inglesa " tobillo ". Ambos están conectados con el proto-indoeuropeo de la raíz * ank- , que significa "doblar" o "arco". [2]
Euclides define un ángulo plano como la inclinación entre sí, en un plano, de dos líneas que se encuentran, y no están rectas una con respecto a la otra. Según Proclus, un ángulo debe ser una calidad o una cantidad, o una relación. El primer concepto fue utilizado por Eudemus , quien consideraba un ángulo como una desviación de una línea recta ; el segundo por Carpus de Antioquía , que lo consideraba como el intervalo o espacio entre las líneas que se cruzan; Euclides adoptó el tercer concepto, aunque sus definiciones de ángulos rectos, agudos y obtusos son ciertamente cuantitativas.
Identificando angulos [ editar ]
En las expresiones matemáticas, es común usar letras griegas ( α , β , γ , θ , φ , ...) para servir como variables que representan el tamaño de algún ángulo. (Para evitar confusiones con su otro significado, el símbolo πgeneralmente no se usa para este propósito). Las letras romanas en minúscula ( a , b , c , ...) también se usan, como las letras romanas en mayúscula en el contexto de polígonos . Vea las figuras en este artículo para ejemplos.
En las figuras geométricas, los ángulos también pueden identificarse por las etiquetas adjuntas a los tres puntos que los definen. Por ejemplo, el ángulo en el vértice A encerrado por los rayos AB y AC (es decir, las líneas desde el punto A al punto B y el punto A al punto C) se denota como ∠BAC (en Unicode U + 2220 ∠ ÁNGULO ) o. A veces, donde no hay riesgo de confusión, el ángulo puede ser referido simplemente por su vértice ("ángulo A").
Potencialmente, un ángulo denotado, por ejemplo, ∠BAC puede referirse a cualquiera de los cuatro ángulos: el ángulo en el sentido de las agujas del reloj desde B hasta C, el ángulo en sentido contrario a las agujas del reloj desde B hasta C, el ángulo en el sentido de las agujas del reloj desde C hasta B o el ángulo en sentido antihorario desde C hasta B , donde la dirección en la que se mide el ángulo determina su signo (consulte Ángulos positivos y negativos ). Sin embargo, en muchas situaciones geométricas es obvio, desde el contexto, que el ángulo positivo es menor o igual a 180 grados, y no existe ambigüedad. De lo contrario, se puede adoptar una convención para que ∠BAC siempre se refiera al ángulo contrario a las agujas del reloj (positivo) de B a C, y a ∠CAB al ángulo contrario a las agujas del reloj (positivo) de C a B.
Tipos de angulos [ editar ]
Angulos individuales [ editar ]
- Un ángulo igual a 0 ° o no girado se denomina ángulo cero.
- Los ángulos más pequeños que un ángulo recto (menos de 90 °) se llaman ángulos agudos ("agudo" significa "agudo").
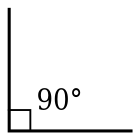
- Un ángulo igual a 14 de vuelta (90 ° o π2 radianes) se llama un ángulo recto . Se dice que dos líneas que forman un ángulo recto son normales , ortogonales o perpendiculares .
- Los ángulos más grandes que un ángulo recto y más pequeños que un ángulo recto (entre 90 ° y 180 °) se llaman ángulos obtusos ("obtuso" que significa "contundente").
- Un ángulo igual a 12 giro (180 ° o pi radianes) se llama un ángulo recto .
- Los ángulos más grandes que un ángulo recto pero menos de 1 vuelta (entre 180 ° y 360 °) se denominan ángulos reflejos .
- Un ángulo igual a 1 vuelta (360 ° o 2 pi radianes) se llama un ángulo completo , ángulo completo , ángulo redondo o una Perigon .
- Los ángulos que no son ángulos rectos o un múltiplo de un ángulo recto se llaman ángulos oblicuos .
Los nombres, intervalos y unidades medidas se muestran en la siguiente tabla:
| Nombre | cero | agudo | ángulo recto | obtuso | Derecho | reflejo | Perigon | |||
| Unidades | Intervalo | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Vueltas | 0 | (0, 14) | 14 | ( 14 , 12) | 12 | ( 12 , 1) | 1 | |||
| Radianes | 0 | (0, 12π) | 12π | ( 12π ,π ) | π | ( π , 2π ) | 2 π | |||
| Grados | 0 ° | (0, 90) ° | 90 ° | (90, 180) ° | 180 ° | (180, 360) ° | 360 ° | |||
| Gons | 0 g | (0, 100) g | 100 g | (100, 200) g | 200 g | (200, 400) g | 400 g | |||
Pares de ángulos de equivalencia [ editar ]
- Los ángulos que tienen la misma medida (es decir, la misma magnitud) se dice que son iguales o congruentes . Un ángulo se define por su medida y no depende de la longitud de los lados del ángulo (por ejemplo, todos los ángulos rectos son iguales en medida).
- Dos ángulos que comparten lados terminales, pero difieren en tamaño por un múltiplo entero de un giro, se denominan ángulos coterminales .
- Un ángulo de referencia es la versión aguda de cualquier ángulo determinado restando repetidamente o la adición de ángulo recto ( 12 a su vez, 180 °, o pi radianes), a los resultados como sea necesario, hasta que la magnitud de resultado es un ángulo agudo, un valor entre 0 y 14 a su vez, 90 °, o pi2 radianes. Por ejemplo, un ángulo de 30 grados tiene un ángulo de referencia de 30 grados, y un ángulo de 150 grados también tiene un ángulo de referencia de 30 grados (180-150). Un ángulo de 750 grados tiene un ángulo de referencia de 30 grados (750–720). [4]
Pares de ángulos verticales y adyacentes [ editar ]
Cuando dos líneas rectas se intersecan en un punto, se forman cuatro ángulos. Por pares, estos ángulos se nombran de acuerdo con su ubicación relativa entre sí.
- Un par de ángulos opuestos entre sí, formados por dos líneas rectas que se intersectan y forman una forma de "X", se denominan ángulos verticales o opuestoso ángulos verticalmente opuestos . Se abrevian como vert. opp ∠s . [5]
- La igualdad de los ángulos verticalmente opuestos se denomina teorema del ángulo vertical . Eudemus de Rodas atribuyó la prueba a Thales de Mileto . [6] [7] La proposición mostró que dado que ambos pares de ángulos verticales son suplementarios a los dos ángulos adyacentes, los ángulos verticales son iguales en medida. Según una nota histórica, [7]cuando Thales visitó Egipto, observó que cada vez que los egipcios dibujaban dos líneas que se cruzaban, medían los ángulos verticales para asegurarse de que eran iguales. Thales concluyó que uno podría probar que todos los ángulos verticales son iguales si aceptara algunas nociones generales, tales como: todos los ángulos rectos son iguales, los iguales sumados a iguales son iguales, y los iguales restados de iguales son iguales.
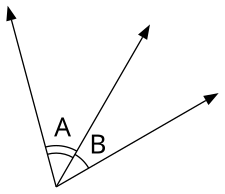
- En la figura, asume la medida del ángulo A = x . Cuando dos ángulos adyacentes forman una línea recta, son suplementarios. Por lo tanto, la medida del ángulo C = 180 - x . Del mismo modo, la medida del ángulo D = 180 - x . Tanto el ángulo C como el ángulo D tienen medidas iguales a 180 - x y son congruentes. Desde ángulo B es complementario a ambos ángulos C y D , cualquiera de estas medidas de los ángulos se pueden usar para determinar la medida del ángulo B . Usando la medida del ángulo C o del ángulo Dencontramos la medida del ángulo B = 180 - (180 - x ) = 180 - 180 + x = x . Por lo tanto, tanto el ángulo A como el ángulo Btienen medidas iguales a x y son iguales en medida.
- Ángulos adyacentes , a menudo abreviados como adj. ∠s , son ángulos que comparten un vértice y un borde comunes pero no comparten ningún punto interior. En otras palabras, son ángulos que están lado a lado, o adyacentes, compartiendo un "brazo". Ángulos adyacentes que suma a un ángulo recto, ángulo recto o el ángulo completo son especiales y se denominan respectivamente complementarios , suplementarios y explementary ángulos (véase "Combinar pares de ángulos" a continuación).
Una transversal es una línea que intersecta un par de líneas (a menudo paralelas) y está asociada con ángulos alternos internos , ángulos correspondientes , ángulos interiores y ángulos exteriores . [8]
Combinando pares de ángulos [ editar ]
Hay tres pares de ángulos especiales que involucran la suma de los ángulos:
- Los ángulos complementarios son pares de ángulos cuyas medidas resumir a un ángulo recto ( 14 a su vez, 90 °, o pi2 radianes). Si los dos ángulos complementarios son adyacentes, sus lados no compartidos forman un ángulo recto. En la geometría euclidiana, los dos ángulos agudos en un triángulo rectángulo son complementarios, porque la suma de los ángulos internos de un triángulo es de 180 grados, y el ángulo recto en sí mismo es de noventa grados.
- El adjetivo complementario es del latín complementum , asociado con el verbo complere , "para rellenar". Un ángulo agudo se "llena" por su complemento para formar un ángulo recto.
- La diferencia entre un ángulo y un ángulo recto se denomina complemento del ángulo. [9]
- Si los ángulos A y B son complementarios, las siguientes relaciones son válidas:
- (La tangente de un ángulo es igual a la cotangente de su complemento y su secante es igual a la cosecantede su complemento.)
- El prefijo " co- " en los nombres de algunas relaciones trigonométricas se refiere a la palabra "complementario".
- Dos ángulos que resumen a un ángulo recto ( 12 a su vez, 180 °, o π radianes) se denominan ángulos suplementarios .
- Si los dos ángulos suplementarios son adyacentes (es decir, tienen un vértice común y comparten solo un lado), sus lados no compartidos forman una línea recta . Tales ángulos son llamados pares lineales de ángulos . [10] Sin embargo, los ángulos suplementarios no tienen que estar en la misma línea y se pueden separar en el espacio. Por ejemplo, los ángulos adyacentes de un paralelogramo son suplementarios, y los ángulos opuestos de un cuadrilátero cíclico (uno cuyos vértices caen todos en un solo círculo) son suplementarios.
- Si un punto P es exterior a un círculo con centro O, y si las líneas tangentes de P tocan el círculo en los puntos T y Q, entonces ∠TPQ y ∠TOQ son suplementarios.
- Los senos de los ángulos suplementarios son iguales. Sus cosenos y tangentes (a menos que no estén definidos) son iguales en magnitud pero tienen signos opuestos.
- En la geometría euclidiana, cualquier suma de dos ángulos en un triángulo es complementaria del tercero, porque la suma de los ángulos internos de un triángulo es un ángulo recto.
- Dos ángulos que se suman a un ángulo completo (1 giro, 360 ° o 2 π radianes) se denominan ángulos complementarios o ángulos conjugados .
- La diferencia entre un ángulo y un ángulo completo se denomina el complemento del ángulo o conjugado de un ángulo.






![{\ displaystyle {\ begin {alineado} & \ sin ^ {2} A + \ sin ^ {2} B = 1 && \ cos ^ {2} A + \ cos ^ {2} B = 1 \\ [3pt] & \ tan A = \ cot B && \ sec A = \ csc B \ end {alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47aa6b35b8e53468f73d7ec051d55371da314fba)
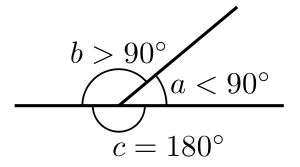

No hay comentarios:
Publicar un comentario