Constante de Coulomb
| Valores de k | Unidades |
|---|---|
| 8.9875517873681764×109 | N·m2/C2 |
| 14.386 | eV Å e-2 |
La constante de Coulomb (denotada  o
o 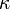 ) es una constante de proporcionalidad en las ecuaciones que relacionan variables eléctricas y es exactamente igual a
) es una constante de proporcionalidad en las ecuaciones que relacionan variables eléctricas y es exactamente igual a  = 8.9875517873681764×109 N·m2/C2 (m/F). Recibe el nombre del físico francés Charles-Augustin de Coulomb (1736–1806).
= 8.9875517873681764×109 N·m2/C2 (m/F). Recibe el nombre del físico francés Charles-Augustin de Coulomb (1736–1806).
 o
o 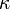 ) es una constante de proporcionalidad en las ecuaciones que relacionan variables eléctricas y es exactamente igual a
) es una constante de proporcionalidad en las ecuaciones que relacionan variables eléctricas y es exactamente igual a  = 8.9875517873681764×109 N·m2/C2 (m/F). Recibe el nombre del físico francés Charles-Augustin de Coulomb (1736–1806).
= 8.9875517873681764×109 N·m2/C2 (m/F). Recibe el nombre del físico francés Charles-Augustin de Coulomb (1736–1806).
A su vez la constante  donde
donde 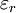 es la permitividad relativa,
es la permitividad relativa,  , y
, y 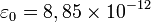 F/m es la permitividad del medio en el vacío.
F/m es la permitividad del medio en el vacío.
 donde
donde 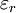 es la permitividad relativa,
es la permitividad relativa,  , y
, y 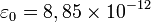 F/m es la permitividad del medio en el vacío.
F/m es la permitividad del medio en el vacío.
Cuando el medio que rodea a las cargas no es el vacío hay que tener en cuenta la constante dieléctrica y la permitividad del material.
La ecuación de la ley de Coulomb queda finalmente expresada de la siguiente manera:
La constante, si las unidades de las cargas se encuentran en Coulomb es la siguiente 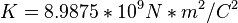 y su resultado será en sistema MKS (
y su resultado será en sistema MKS ( ). En cambio, si la unidad de las cargas están en UES (q), la constante se expresa de la siguiente forma
). En cambio, si la unidad de las cargas están en UES (q), la constante se expresa de la siguiente forma  y su resultado estará en las unidades CGS
y su resultado estará en las unidades CGS  .
.
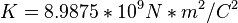 y su resultado será en sistema MKS (
y su resultado será en sistema MKS ( ). En cambio, si la unidad de las cargas están en UES (q), la constante se expresa de la siguiente forma
). En cambio, si la unidad de las cargas están en UES (q), la constante se expresa de la siguiente forma  y su resultado estará en las unidades CGS
y su resultado estará en las unidades CGS  .
.
En 1785, Charles Augustin de Coulomb (1736-1806), físico e ingeniero francés que también enunció las leyes sobre el rozamiento, presentó en la Academia de Ciencias de París, una memoria en la que se recogían sus experimentos realizados sobre cuerpos cargados, y cuyas conclusiones se pueden resumir en los siguientes puntos:
- Los cuerpos cargados sufren una fuerza de atracción o repulsión al aproximarse.
- El valor de dicha fuerza es proporcional al producto del valor de sus cargas.
- La fuerza es de atracción si las cargas son de signo opuesto y de repulsión si son del mismo signo.
- La fuerza es inversamente proporcional al cuadrado de la distancia que los separa.
Estas conclusiones constituyen lo que se conoce hoy en día como la ley de Coulomb.
La fuerza eléctrica con la que se atraen o repelen dos cargas puntuales en reposo es directamente proporcional al producto de las mismas, inversamente proporcional al cuadrado de la distancia que las separa y actúa en la dirección de la recta que las une.
donde:
- F es la fuerza eléctrica de atracción o repulsión. En el S.I. se mide en Newtons (N).
- Q y q son lo valores de las dos cargas puntuales. En el S.I. se miden en Culombios (C).
- r es el valor de la distancia que las separa. En el S.I. se mide en metros (m).
- K es una constante de proporcionalidad llamada constante de la ley de Coulomb. No se trata de una constante universal y depende del medio en el que se encuentren las cargas. En concreto para el vacío k es aproximadamente 9·109 N·m2/C2 utilizando unidades en el S.I.
Si te fijas bien, te darás cuenta que si incluyes el signo en los valores de las cargas, el valor de la fuerza eléctrica en esta expresión puede venir acompañada de un signo. Este signo será:
- positivo. cuando la fuerza sea de repulsión (las cargas se repelen). ( + · + = + o - · - = + )
- negativo. cuando la fuerza sea de atracción (las cargas se atraen). ( + · - = - o - · + = - )
Por tanto, si te indican que dos cargas se atraen con una fuerza de 5 N, no olvides que en realidad la fuerza es -5 N, porque las cargas se atraen.
Expresión vectorial de la fuerza eléctrica
La fuerza eléctrica descrita en la ley de Coulomb no deja de ser una fuerza y como tal, se trata de una magnitud vectorial que en el Sistema Internacional de Unidades se mide en Newtons (N). Su expresión en forma vectorial es la siguiente:
donde el nuevo valor u⃗ r es un vector unitario en la dirección que une ambas cargas. Observa que si llamamos r⃗ al vector que va desde la carga que ejerce la fuerza hacia la que la sufre, u⃗ r es un vector que nos indica la dirección de r⃗
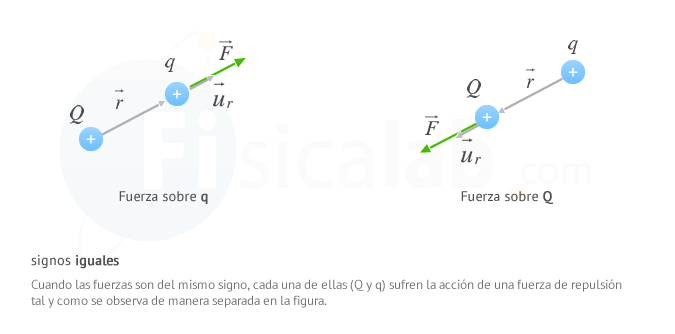
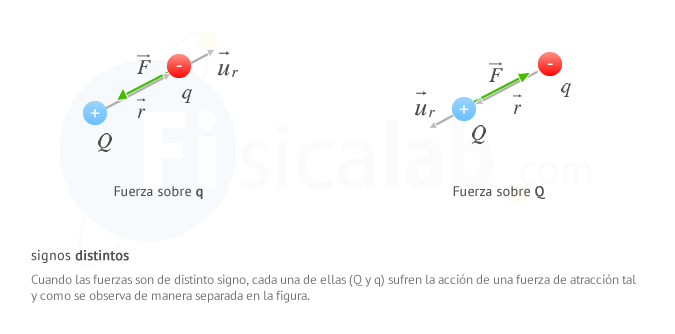
Date cuenta que la fuerza electrica siempre tiene la misma dirección que el vector unitario u⃗ r y el mismo sentido si tienen el mismo signo y sentido opuesto si tienen signo distinto.
No olvides que debes incluir el signo de las cargas cuando utilices la expresión de la ley de Coulomb.
| ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||
Esto equivale a decir que la atracción o la repulsión que puede ejercer la carga q1 sobre la carga q2 es la misma en todos los puntos de una esfera de superficie S=4pr2 centrada en q1. La fuerza disminuye al alejarnos hacia esferas de mayor superficie y, por lo tanto, planteamos que su módulo ha de ser inversamente proporcional a la cantidad 4pr2.
| ||||||||||||||||||||||||||
Finalmente, se ha de considerar la influencia del medio, puesto que la interacción eléctrica no se transmite igual, por ejemplo, en el vacío que en el aire o en el agua. A tal fin, se introduce una constante, e, llamada permitividad eléctrica. La constante se escribe en el denominador de la expresión que calcula la fuerza, con lo que un medio con permitividad alta transmite mal la interacción eléctrica (es un medio "no eléctrico" o dieléctrico) y un medio con permitividad baja la transmite bien (es un medio conductor).
| ||||||||||||||||||||||||||
El conjunto de estos razonamientos conduce a la expresión operativa de la ley de ley de Coulomb:
| ||||||||||||||||||||||||||
|
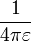
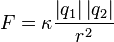
No hay comentarios:
Publicar un comentario