Gráficas de M.R.U.
Gráfica posición-tiempo (x-t)
La gráfica posición-tiempo (x-t) de un movimiento rectilíneo uniforme (m.r.u.). representa en el eje horizontal (eje x) el tiempo y en el eje vertical la posición. Observa como la posición (normalmente la coordenada x) aumenta (o disminuye) de manera uniforme con el paso del tiempo. Podemos distinguir dos casos, cuando la velocidad es positiva o negativa:
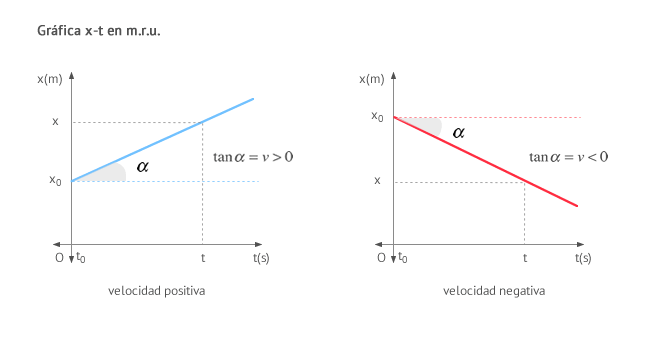
A partir del ángulo α puedes obtener la velocidad. Recuerda para ello que, en un triángulo rectángulo se define la tangente de uno de sus ángulos como el cateto opuesto partido cateto contiguo:
El valor de la pendiente es la propia velocidad. Por tanto a mayor pendiente de la recta, mayor velocidad posee el cuerpo.
Gráfica velocidad-tiempo (v-t)
La gráfica velocidad-tiempo (v-t) de un movimiento rectilíneo uniforme (m.r.u.) muestra que la velocidad permanece constante a lo largo del tiempo. De nuevo, podemos distinguir dos casos:
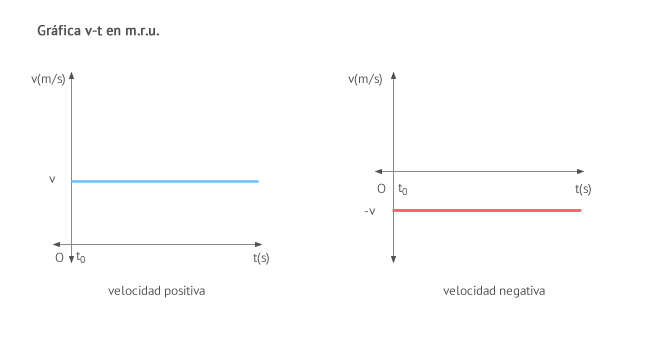
Observa que el área que limitada bajo la curva v entre dos instantes de tiempo es el espacio recorrido.
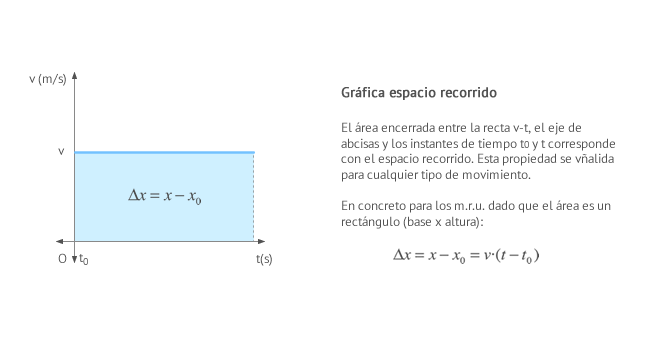
En este caso resulta inmediato calcular dicha área, al tratarse de un rectángulo. Pero, ¿sabrías qué herramienta matemática permite el cálculo de áreas bajo una curva, sea cual sea su forma?
Gráfica aceleración-tiempo (a-t)
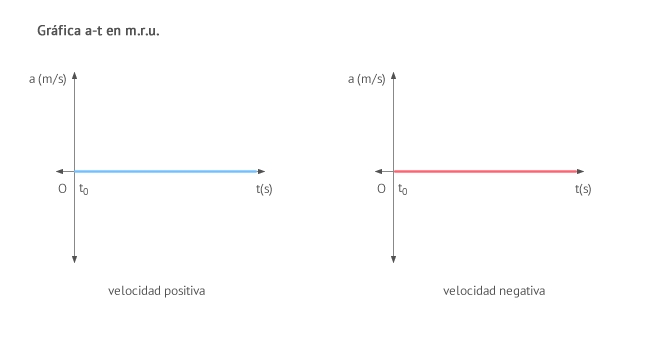
La gráfica aceleración-tiempo (a-t) de un movimiento rectilíneo uniforme (m.r.u.) muestra que la aceleración es nula en todo momento. En este caso, tanto si la velocidad del cuerpo se considera positiva como negativa, tenemos una sola posibilidad, ilustrada en la figura:
Ejemplo
Determina las gráficas de los siguientes movimientos rectilíneos uniformes:
- x = 3 + 4·t
- x = 3 - 4·t
- x = -3 + 4·t
- x = -3 - 4·t
- 3·x = 9 + 12·t
Donde x se mide en metros y t en segundos.
Solución
Consideraciones previas
- Podemos identificar cada una de las expresiones anteriores con la expresión general del movimiento rectilíneo uniforme
x=x0+v⋅t - El término independiente se corresponde con la posición inicial de cada movimiento x0
- El término que acompaña a t corresponde con la velocidad del cuerpo según la expresión general. No olvides que la velocidad instantánea de un cuerpo se define como la derivada respecto al tiempo de la posición, por tanto:
- Recuerda que en cualquier movimiento rectilíneo uniforme la aceleración es cero. La aceleración instantánea se define como la derivada de la velocidad respecto al tiempo. Dado que la velocidad es constante, la derivada de una constante es cero. Por ejemplo, para el primer movimiento:
- Recuerda que la posición, la velocidad y la aceleración son magnitudes vectoriales. En el caso de que la trayectoria sea una recta, podemos usar el convenio de signos en movimientos rectilíneos habitual para usar escalares (números) en lugar de vectores
- La ecuación 5 no está escrita de la forma general del m.r.u, por lo que tenemos que manipularla: pasamos el factor que acompaña a la x a la derecha quedando:
Observa que ahora tenemos una expresión igual que la del primer movimiento. Por tanto sus gráficas también serán iguales
Resolución
Gráficas de posición
Para determinar la gráfica de posición de cada movimiento, basta dar un par de valores a t, obtener los valores correspondientes de x y dibujar la recta. Nos queda:
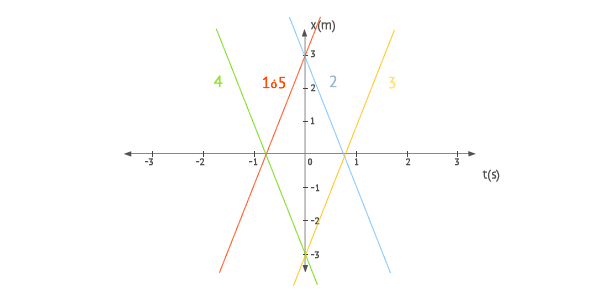
Gráficas de velocidad
La velocidad es constante en todos los movimientos, sus gráficas, por tanto son rectas horizontales:
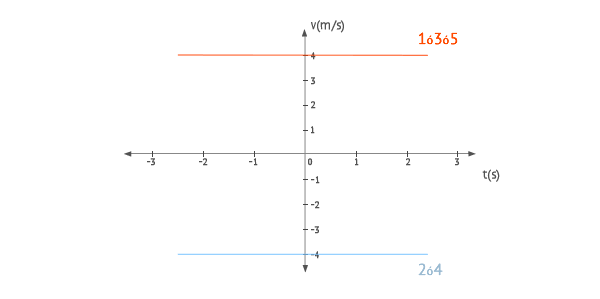
Gráficas de aceleración
Las gráficas de aceleración de todos los movimientos son iguales.
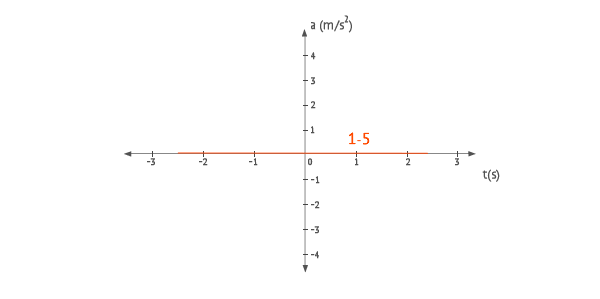
No hay comentarios:
Publicar un comentario