Física y química en 3 º de la ESO

Los gases y la Teoría Cinética: presión

1. Presión

Llamaremos "presión" a la fuerza por unidad de superficie que ejercen las partículas del gas al chocar contra las paredes del recipiente.

1.1 Unidades

Se define la magnitud física llamada Presión como una fuerza por unidad de superficie, es decir:

Su unidad en el Sistema Internacional, es el Pascal (Pa) y equivale a la presión que ejerce una fuerza de 1 newton sobre una superficie de 1 m²normal a la misma:

El Pa es una unidad de presión muy pequeña, por lo que se suelen usar otras unidades de presión. Entre ellas tenemos:

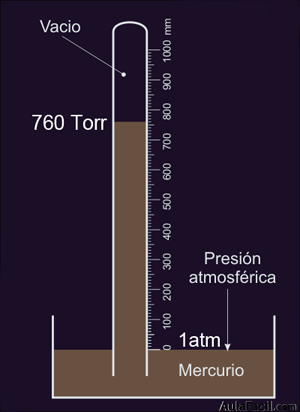
La atmósfera cuyo símbolo será atm y que equivale a una cantidad de Pascales de: 1 atm = 101.325 Pa, o lo que es lo mismo, 1013 hPa (hectopascal). El hPa se llamaba antes milibar.

Por último también se utiliza el Torr (Evangelista Torricelli) que equivale a la presión ejercida en la base de una columna de un milímetro de altura de mercurio, con lo que: 1 atm = 101325 Pa = 1013 hPa = 760 Torr

1.2 Factores que regulan la presión

La presión que ejerce un gas sobre las paredes del recipiente, depende de tres factores:

• 1. Del nº de partículas de gas (cantidad de gas considerada). A más partículas más presión.
• 2. Del volumen del recipiente. A mayor volumen, menor presión.
• 3. De la temperatura del gas. A mayor temperatura, mayor velocidad de las partículas del gas y por tanto mayor presión.

En esta sección estudiaremos un sistema de muchas partículas y consideraremos la conducta promedio de sus constituyentes microscópicos. En particular, se calculará la presión ejercida por el sistema de partículas en términos de los choques que experimentan las moléculas del gas contra las paredes del recipiente.
El objetivo del programa, es el de relacionar las variables presión, volumen y temperatura, en un modelo de gas ideal bidimensional, así como la de conocer la interpretación cinética de la presión y de la temperatura de un gas.
El gas ideal bidimensional está encerrado en un recipiente que dispone de un émbolo móvil, de modo que se puede aumentar o disminuir el volumen (área) del gas. Las moléculas se colocan inicialmente en posiciones aleatorias, las direcciones de sus velocidades también son aleatorias y sus magnitudes son iguales y proporcionales a la raíz cuadrada de la temperatura. Tenemos de este modo un sistema de partículas en equilibrio a la temperatura T, que chocan elásticamente entre sí y con las paredes del recipiente.
El programa calcula el cambio de momento lineal que experimentan las moléculas al chocar con el émbolo y divide este cambio entre el tiempo. El cociente es una medida de la fuerza que ejerce el émbolo sobre las moléculas del gas, o también se puede interpretar como una medida de la presión del gas.
El programa interactivo, también nos permite observar el vector velocidad asociado a cada molécula y cómo dicho vector cambia de orientación pero no de módulo cuando una molécula choca con la pared del recipiente, pero cambia de módulo y dirección cuando se produce una colisión entre dos moléculas.
Vemos que partiendo de una distribución inicial en el que las velocidades de las moléculas son iguales en módulo, al cabo de un cierto tiempo unas moléculas tienen mayor velocidad y otras moléculas tienen menor velocidad. La distribución de velocidades cuando se alcanza el equilibrio sigue la ley de distribución de Maxwell.

Descripción

El postulado básico de la teoría cinética de los gases es que las direcciones y las magnitudes de las velocidades de las moléculas están distribuidas al azar.
Cuando nos referimos a las velocidades de las moléculas, las medimos respecto del centro de masas del sistema gaseoso, por tanto, la presión y la temperatura del gas no se modifican si el recipiente que lo contiene está en movimiento.
Si suponemos que las velocidades en el sentido positivo del eje X (o del eje Y o Z) son igualmente probables que en el sentido negativo, las velocidades medias a lo largo de los ejes son cero, es decir.
x

>=y>=z>=0.Por otra parte, se cumplirá que las velocidades a lo largo del eje X no estarán relacionadas con las velocidades a lo largo del eje Y o Z, por tanto,
2_x>=2_y>=2_z>.Como el cuadrado del módulo de la velocidad es v²= v²_x +v²_y +v²_z resulta que < v²>=3< v²_x>

La presión ejercida por el gas

Supongamos que el gas está encerrado en un recipiente, tal como se muestra en la figura. El recipiente dispone de un émbolo móvil de área A. Para mantener fijo el émbolo es necesario ejercer una fuerza F, normalmente a la superficie del émbolo. El valor de la fuerza F es igual al producto de la presión ejercida por el gas por el área del émbolo.
F=PA

Las moléculas del gas chocan elásticamente con el émbolo, de modo que la componente X de la velocidad cambia de sentido. Por tanto, el cambio en el momento lineal de cada molécula es
Dp=2mv_x

Si el número total de moléculas que chocan con el émbolo en el intervalo de tiempo comprendido entre t y t+Dt es N_x, la variación de momento lineal será 2mv_xN_x.
Podemos calcular N_x considerando que solamente la mitad de las moléculas, en promedio, tienen el sentido de la velocidad hacia la parte positiva del eje X, es decir, se dirigen hacia el émbolo.
Si suponemos que las moléculas que chocan con el émbolo tienen el mismo valor de la componente X de la velocidad, cruzarán el área A en el tiempo Dt todas las partículas contenidas en el volumen Av_xDt. Si n es el número de partículas por unidad de volumen N_x valdrá entonces, nAv_xDt/2.

La variación de momento lineal Dp en el intervalo de tiempo comprendido entre t y t+Dt es mv_x nAv_xDt.
La fuerza sobre el émbolo es el cociente entre el cambio de momento lineal y el tiempo que tarda en efectuarse dicho cambio.

y por tanto, la presión ejercida por el gas vale
P=n(mv²_x)
Todas las moléculas no tienen el mismo valor v_x de la velocidad, sino que la distribución de velocidades es tal que su valor medio cuadrático es 2
_x>. Por tanto, en la expresión de la presión P, hemos de sustituir v²_x por 2_x>. (1)
ya que 2
_x>=2>/3El último término que aparece en la fórmula es el valor medio de la energía cinética.

Definición cinética de la temperatura

La temperatura de un sistema se define en Termodinámica como una variable que se mide por los cambios observados en las propiedades macroscópicas de la materia cuando cambia la temperatura. La ecuación de estado de un gas ideal relaciona las propiedades macroscópicas, presión P, el volumen V y temperatura T.
PV=mRTSiendo m el número de moles.
El número n de moléculas por unidad de volumen se obtiene dividiendo el número total de moléculas N entre el volumen del recipiente V.

donde N₀ el número de Avogadro
Introduciendo n en la expresión de la presión del gas (1), obtenemos
                (2)
Comparando esta ecuación con la de estado de un gas ideal, se llega a la definición cinética de temperatura

El cociente entre las dos constantes R y N₀ es otra constante que designamos por k, la constante de Boltzmann.

La temperatura absoluta definida, por ejemplo, para un termómetro de gas ideal es una medida directa de la energía media de traslación de las moléculas del gas.
                       (3)
La temperatura podría medirse en unidades de energía, el hecho de que se mida en grados se debe a la definición tradicional de temperatura, que se estableció antes de que se descubriese la relación antes mencionada.
Otra forma útil de la ecuación de los gases perfectos que se deriva de (2) y (3) es
P·V=N·k·T
Donde N es el número de moléculas contenidas en el recipiente de volumen V.
Como las moléculas de un gas ideal solamente tienen energía cinética, se desprecia la energía potencial de interacción. La energía interna U de un gas ideal es N veces la energía cinética media de una molécula.


http://www.sc.ehu.es/sbweb/fisica/estadistica/gasIdeal/gasIdeal.html

La teoría cinética de los gases explica las características y propiedades de la materia en general, y establece que el calor y el movimiento están relacionados, que las partículas de toda materia están en movimiento hasta cierto punto y que el calor es una señal de este movimiento. La teoría cinética de los gases considera que los gases están compustos por las moléculas, partículas discretas, individuales y separadas. La distancia que existe entre estas partículas es muy grande comparada con su propio tamaño, y el volumen total ocupado por tales corpúsculos es sólo una fracción pequeña del volumen ocupado por todo el gas. por tanto, al considerar el volumen de un gas debe tenerse en cuenta en primer lugar un espacio vacío en ese volumen. El gas deja muchos espacios vacíos y esto explica la alta comprensibilidad, la baja densidad y la gran miscibilidad de unos con otros. Hay que tener en cuenta que: 1. No existen fuerzas de atracción entre la moléculas de un gas. 2. Las moléculas de los gases se mueven constantemente en línea recta por lo que poseen energía cinética. 3. En el movimiento, las moléculas de los gases chocan elásticamente unas con otras y con las paredes del recipiente que las contiene en una forma perfectamente aleatoria. 4. La frecuencia de las colisiones con las paredes del recipiente explica la presión que ejercen los gases. 5. La energía de tales partículas puede ser convertida en calor o en otra forma de energía. pero la energía cinética total de las moléculas permanecerá constante si el volumen y la temperatura del gas no varían; por ello, la presión de un gas es constante si la temperatura y el volumen no cambian.

http://ensenarquimica.galeon.com/aficiones2063281.html