Condiciones de contorno del campo electromagnético
Las Ecuaciones de Maxwell describen el comportamiento de los campos electromagnéticos: campo eléctrico  , campo magnético (oinducción magnética)
, campo magnético (oinducción magnética)  , desplazamiento eléctrico
, desplazamiento eléctrico 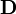 e intensidad de campo magnético
e intensidad de campo magnético  . Las formas diferenciales de estas ecuaciones requieren que haya siempre un entorno abierto alrededor del punto al cual estos campos están siendo estudiados, de otra manera, los campos vectoriales E, D, B y H no son diferenciables. En otras palabras, el medio tiene que ser continuo. Obviamente, en la frontera de dos medios con valores diferentes de permitividad eléctrica y Permeabilidad magnética, esta condición no se aplica.
. Las formas diferenciales de estas ecuaciones requieren que haya siempre un entorno abierto alrededor del punto al cual estos campos están siendo estudiados, de otra manera, los campos vectoriales E, D, B y H no son diferenciables. En otras palabras, el medio tiene que ser continuo. Obviamente, en la frontera de dos medios con valores diferentes de permitividad eléctrica y Permeabilidad magnética, esta condición no se aplica.
 , campo magnético (oinducción magnética)
, campo magnético (oinducción magnética)  , desplazamiento eléctrico
, desplazamiento eléctrico 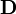 e intensidad de campo magnético
e intensidad de campo magnético  . Las formas diferenciales de estas ecuaciones requieren que haya siempre un entorno abierto alrededor del punto al cual estos campos están siendo estudiados, de otra manera, los campos vectoriales E, D, B y H no son diferenciables. En otras palabras, el medio tiene que ser continuo. Obviamente, en la frontera de dos medios con valores diferentes de permitividad eléctrica y Permeabilidad magnética, esta condición no se aplica.
. Las formas diferenciales de estas ecuaciones requieren que haya siempre un entorno abierto alrededor del punto al cual estos campos están siendo estudiados, de otra manera, los campos vectoriales E, D, B y H no son diferenciables. En otras palabras, el medio tiene que ser continuo. Obviamente, en la frontera de dos medios con valores diferentes de permitividad eléctrica y Permeabilidad magnética, esta condición no se aplica.
Sin embargo, las condiciones de contorno (o de frontera) para los distintos campos electromagnéticos pueden ser deducidas a partir la forma integral de las ecuaciones de Maxwell.- ...............................:https://es.wikipedia.org/w/index.php?title=Condiciones_de_contorno_del_campo_electromagn%C3%A9tico&printable=yes
PROPIEDADES DE LOS CONDUCTORES
En sentido amplio los materiales se dividen, de acuerdo con sus propiedades eléctricas, en conductores y no conductores. Los materiales no conductores se denominan aisladores o dieléctricos según su conductividad, mohs por metro o siemens por metro. la conductividad de un material depende usualmente de la temperatura y la frecuencia un material de alta conductividad (s>>1) se denomina metal; uno de baja conductividad(s<<1 span=""> aislador y uno de conductividad intermedia semiconductor.
La conductividad de los metales suele aumentar al disminuir la temperatura. en una temperatura cercana al cero absoluto (T=0°K) algunos conductores exhibe conductividad infinita motivo por el cual se le llama superconductores. El plomo y el aluminio son ejemplos representativos de esos materiales.
| Movimiento de electrones |
Microscópicamente , la principal diferencia entre un metal y un aislador radica en la cantidad de electrones disponibles para la conducción de la corriente. Los materiales dieléctricos poseen pocos electrones disponibles para la conducción de corriente en contraste con los metales que poseen abundantes electrones libres.
En materiales como los metales, algunos electrones no se hallan ligados a sus átomos individuales, sino que son libres de moverse a través del material: en efecto son compartidos por todos los átomos
| Átomos ligados |
Esas partículas sueltas reciben el nombre de electrones de “conducción”. En un metal como el cobre, aproximadamente un electrón por átomo es de ese tipo. Los metales son los conductores más comunmente usados.
Los metales suelen ser duros y resistentes, aunque existen ciertas variaciones de uno a otro tienen algunas de las siguientes propiedades; dureza o resistencia, elasticidad o capacidad de volver a su forma original después de sufrir deformación, maleabilidad o posibilidad de cambiar de forma, resistencia a la fatiga o capacidad de soportar una fuerza y ductilidad o posibilidad de deformarse sin sufrir roturas.
Los campos eléctricos de los electrones en los materiales no son neutralizados por ninguna carga positiva, así que los electrones se aceleran alejándose unos de otros. Esto continúa hasta que los electrones alcanzan una de las superficies del conductor o hasta que un número de electrones igual al de los electrones introducidos alcanzan la superficie.
Aquí la salida de los electrones es detenida por el material que rodea al conductor suponiendo que es un aislante que no posee la banda de conducción apropiada. Ninguna carga permanece dentro del conductor. Si así tratara de hacerlo el campo eléctrico resultante, obligaría a las cargas a permanecer en la superficie.
Para una situación electrostática, no existen ni cargas ni campos eléctricos en ningún punto dentro de un conductor. Sin embargo, la carga puede aparecer en la superficie como una densidad de carga superficial.
La ley de Gauss nos dice que el flujo eléctrico que abandona una superficie pequeña debe ser igual a la carga que se encuentra en ella. El flujo no puede salir en una dirección tangencial ya que se componente es cero, por lo que lo debe hacer normal a la superficie.
CORRIENTE DE CONVECCIÓN Y DE CONDUCCIÓN
La corriente eléctrica es causada debido a al movimiento de cargas, la corriente a través de una zona determinada es la carga eléctrica que pasa a través de superficie por unidad de tiempo.
Es decir,
Así, en una carga de corriente de un amperio, se transfiere una taza de un columb por segundo.
Ahora introducimos el concepto de densidad de corriente J. si una corriente ∆I fluye a través de una superficie ∆S, como la densidad de corriente es
o
Asumiendo que la densidad de corriente es perpendicular a la superficie. Si la densidad de corriente no es normal a la superficie,
Así, la corriente total a través de una superficie S es
Según como se produzca I, existen diferentes tipos de densidad de corriente: densidad de corriente de convección, densidad de de corriente de conducción y densidad de corriente de desplazamiento.
La corriente de convección, en cuanto que distinta de la corriente de conducción, no implica conductores y en consecuencia no satisface la ley de ohm. Ocurre cuando la corriente fluye a través de un medio aislador como líquido, gas enrarecido o en el vacio.Un haz de electrones (ver video) por ejemplo es una corriente por convección.
Las Corrientes de conducción son el resultado del movimineto de deriva de los portadores de carga bajo la influencia de un campo eléctrico aplicado
la corriente a través del filamento es
La densidad de corriente eléctrica se define como una magnitud vectorial que tiene unidades de corriente eléctrica por unidad de superficie ,es decir, intensidad por unidad de área.
La densidad de corriente en un punto dado es el área normal de corriente a través de una unidad en ese punto.
La dirección y en la densidad de corriente Jy está dada por
La conducción actual requiere de un conductor. Un conductor se caracteriza por una gran cantidad de electrones libres que proporcionan corriente de conducción por un campo eléctrico impresionado.
Cuando se aplica un campo eléctrico E, la fuerza de un electrón con carga -e es
Según la ley de Newton, el cambio promedio en el impulso de los electrones libres debe coincidir con la fuerza aplicada. Así,
o
donde τ es el intervalo de tiempo promedio entre colisiones.
Si no hay electrones n por unidad de volumen, la densidad de carga electrónica viene dada por
Así, la densidad de corriente de conducción es
o
Un conductor perfecto no puede contener un campo electrostático en su interior.
Según la ley de Gauss, si E = 0, la densidad de carga ρv debe ser cero. Llegamos a la conclusión de nuevo que un conductor perfecto no puede contener un campo electrostático en su interior. , En condiciones estáticas,
La dirección del campo eléctrico E producido es la misma que la dirección del flujo de cargas positivas o corriente I. Esta dirección es opuesta a la dirección del flujo de electrones. El campo eléctrico aplicado es uniforme y su magnitud está dada por
Dado que el conductor tiene una sección transversal uniforme,
Sustituyendo
Por lo tanto
o
La Potencia P se define como la tasa de cambio de la energía W o fuerza por la velocidad. Por lo tanto,
o
que se conoce como ley de Joule.
Para un conductor con sección transversal uniforme, dv = dS dl, por lo que la ecuación se convierte en
o
POLARIZACIÓN EN DIELÉCTRICOS
| Polarización de un dieléctrico |
Considérese un dieléctrico, no electrizado, cuyas moléculas son polares y está alejado de influencias eléctricas externas.
En estas condiciones, las moléculas de esta sustancia están distribuidas al azar, como se representa en la figura A. Al acercar a este dieléctrico un cuerpo electrizado (por ejemplo, con carga positiva), la carga de este último actuará sobre las moléculas del aislante, haciendo que se orienten y alineen en la forma indicada en la figura B. Cuando esto sucede, se dice que el dieléctrico está polarizado. La figura C muestra que el efecto final de esta polarización consiste en hacer aparecer cargas negativas y positivas distribuidas tal como se ve en la ilustración. Obsérvese que aún cuando la carga total del dieléctrico es nula, la polarización hace que se manifiesten cargas eléctricas de signos opuestos de manera similar a lo que sucede cuando se carga un conductor por inducción.
Si el dieléctrico estuviera constituido por moléculas apolares, se observaría el mismo efecto final, ya que con la aproximación del cuerpo electrizado, las moléculas se volverían polares y, por consiguiente, se alinearían como se muestra en la figura B.
La principal característica entre un conductor y un dieléctrico esta en la disponibilidad de electrones libres en la capa atómica externa para conducir una corriente, las cargas que existen en un dieléctrico no pueden moverse libremente, están ligadas por fuerzas finitas y se puede esperar un desplazamiento cuando se aplican fuerzas externas .
La polarización se establece como la generación de momentos de dipolos dados por:
| Generación de dipolos |
donde p es el vector de distancia -Q a + Q del dipolo. Si hay dipolos N en un volumen ∆v. del momento dieléctrico, el dipolo total debido al campo eléctrico es
Como una medida de la intensidad de la polarización, definimos P de polarización como el momento dipolar por unidad de volumen del dieléctrico, es decir,
Así, podemos concluir que el principal efecto del campo eléctrico E en un dieléctrico es la creación de los momentos dipolares que se alinean en la dirección de E.
El potencial dV en un punto 0 exterior debido al momento P de los dipolos dv' es
donde R^2 = (x - x ')^2 + (y - y')^2 + (z - z ')^2 y R es la distancia entre el elemento de volumen dv' en (x’, y’, z’) y el campo en el punto 0 (x, y, z). Podemos transformar la ecuación en una forma que facilita la interpretación física. Se demuestra fácilmente que el gradiente de 1/R con respecto a las coordenadas está preparado por
Asi,
La aplicación de la identidad vectorial
la integración en el volumen total v' del dieléctrico, se obtiene
Aplicando el teorema de la divergencia al primer término conduce finalmente a
donde a'n es la unidad externa normal a la superficie dS' del dieléctrico. La comparación de los dos términos en el lado derecho de la ecuación con normas de calidad ambiental muestra que los dos términos denotan el potencial debido a la superficie y distribución de la carga de volumen con densidades
En otras palabras, cuando se produce la polarización, una densidad de volumen de carga equivalente ρpv se forma a lo largo del dieléctrico, mientras que una densidad de carga equivalente de superficie ρPS está formada sobre la superficie del dieléctrico. Nos referimos a ρPS y ρpv como dependiente de superficie y densidades de carga de volumen, respectivamente, a diferencia de la superficie libre y la densidad de volumen de carga ρs y ρv. Las cargas libres son aquellas que son capaces de mover a distancia macroscópicas como los electrones en un conductor, que son las cosas de control. El total de carga de la envolvente positivo en la superficie S que limita el dieléctrico es
mientras las cargas que permanecen en el interior de S son
Así, la carga total del material dieléctrico es cero, es decir,
\[
Carga\ Total = \oint_S {{\rho _{ps}}dS + \int\limits_v {{\rho _{pv}}dv = Q_b - Q_b = 0
\]
Si ρv es la carga libre de la densidad de volumen, el total de volumen de la densidad de carga p, viene dada por
por lo tanto
dónde
Sería de esperar que la polarización P variará directamente como la aplicación de campo eléctrico E. Para algunos dieléctricos, este suele ser el caso y hemos
donde xe, conocida como la susceptibilidad eléctrica del material, es más o menos una medida de cuán sensibles un determinado dieléctrico es a campos eléctricos.
DISRUPCIÓN ELÉCTRICA
En la práctica no existen dieléctricos ideales por lo tanto se puede aplicar un campo eléctrico lo suficientemente grande de tal modo que se puedan extraer electrones de las moléculas convirtiendo el dieléctrico en conductor en ese momento se puede decir que existió disrupción eléctrica, que puede ocurrir en cualquier material dieléctrico dependiendo su naturaleza, la temperatura, la humedad y el tiempo de exposición al campo eléctrico.
El siguiente es un video que muestra el momento en el que se produce la disrupción eléctrica del aire que se puede producir con una tensión de 30Kv/cm a una atmósfera de presión y al nivel del mar.
CONDICIONES EN LA FRONTERA
Si el campo existe en una región compuesta por dos medios diferentes, las condiciones que el campo debe cumplir en la interfaz que separa los medios de comunicación se denominan condiciones de frontera. Estas condiciones son útiles para determinar el ámbito de un lado de la frontera si se conoce el campo en el otro lado. Obviamente, las condiciones serán dictadas por el tipo de material de los medios de comunicación que están hechos. Vamos a considerar las condiciones de frontera en una interfaz que separa
- dieléctrico (εr1) y dieléctrico (εr2)
- conductores y dieléctricos
- conductor y espacio libre
Para determinar las condiciones de frontera, tenemos que utilizar las ecuaciones de Maxwell:
y
También tenemos que descomponer la intensidad del campo eléctrico E en dos componentes ortogonales:
| Condiciones de la frontera |
Sean ambos medios definidos por sus permitividades eléctricas 1 y 2, o bien, en términos de sus constantes dieléctricas K1 y K2. En el medio 1 está definido un campo eléctrico E y un vector desplazamiento dieléctrico D y que se relacionan linealmente según
similar situación se presenta en el dieléctrico 2
Con el empleo de la ley de Gauss se obtiene información acerca de la componente normal de los campos; en efecto, si se elige como superficie gaussiana un cilindro con su eje perpendicular a la superficie interfacial ( ver figura) y cuyo manto tiene una longitud infinitamente pequeña, entonces sólo existirá flujo a través de las tapas del cilindro gaussiana; si son los respectivos versores áreas de las tapas, se tiene que:
| Superficie Gaussiana |
suponiendo que el camino es muy pequeño con respecto a la variación de E. Obtenemos
donde
Así, las componentes tangenciales de E son las mismas en los dos lados de la frontera En otras palabras, Et no sufre ningún cambio en la frontera y se dice que continua a través de la frontera. Desde D = εE = Dt + Dn,
o
es decir, Dt sufre algún cambio a través de la interfaz. Por lo tanto Dt se dice que es discontinuo a través de la interfaz.
∆h → 0 da
o
Si no existen cargas libres en la interfaz (es decir, las cargas no son deliberadamente colocadas allí), ρS = 0 y la ecuación anterior se convierte en
Así, la componente normal de D es continua a través de la interfaz, es decir, Dn no sufre ningún cambio en la frontera. Puesto que D = εE, la ecuación anterior puede escribirse como
muestran que la componente normal de E es discontinua en la frontera. Como se mencionó anteriormente, las condiciones de frontera se aplican generalmente en la búsqueda del campo eléctrico en un lado de la frontera dado el ámbito en el otro lado. Además de esto, podemos usar las condiciones de frontera para determinar la refracción del campo eléctrico a través de la interfaz.
Considere D1 o E1 y E2 o D2 que forman ángulos θ1 y θ2 con la normal a la interfaz
o
Del mismo modo
o
Dividiendo la ecuación, da
Desde ε1 = ε0εr1 y ε2 = ε0εr2,
Para determinar las condiciones límite para una interfaz conductor-dieléctrico, seguimos el mismo procedimiento utilizado para la interfaz dieléctrico-dieléctrico, salvo que se integre el hecho de que E = 0 dentro del conductor.
Como ∆h→0
Del mismo modo,
porque D = εE = 0 dentro del conductor.
o
1. El campo eléctrico no puede existir dentro de un conductor, es decir,
2. Dado que E = - ▼E = 0, no puede haber una diferencia de potencial entre dos puntos cualesquiera del conductor, es decir, un conductor es un cuerpo potencial.
3. El campo eléctrico E puede ser externo al conductor y normal a su superficie, es decir
Las condiciones de contorno en la interfaz entre un conductor y el espacio libre se puede obtener de la ecuación anterior, sustituyendo εr por 1 (porque el espacio libre puede ser considerado como un dieléctrico especial para la que εr = 1). Esperamos que el campo eléctrico E externo al conductor y normal a su superficie. Así, las condiciones de contorno son
No hay comentarios:
Publicar un comentario