El triángulo de Kepler es un triángulo rectángulo con lados en progresión geométrica. La relación entre lados de un triángulo de Kepler, está vinculada al número áureo.1 2
y puede ser escrita:  , o aproximadamente 1 : 1,272 : 1,618.3 Los cuadrados de los lados de éste triángulo (véase fig. tk1) están en progresión geométrica de acuerdo al número áureo.- ........................................................................:https://es.wikipedia.org/w/index.php?title=Tri%C3%A1ngulo_de_Kepler&printable=yes
, o aproximadamente 1 : 1,272 : 1,618.3 Los cuadrados de los lados de éste triángulo (véase fig. tk1) están en progresión geométrica de acuerdo al número áureo.- ........................................................................:https://es.wikipedia.org/w/index.php?title=Tri%C3%A1ngulo_de_Kepler&printable=yes
 , o aproximadamente 1 : 1,272 : 1,618.3 Los cuadrados de los lados de éste triángulo (véase fig. tk1) están en progresión geométrica de acuerdo al número áureo.- ........................................................................:https://es.wikipedia.org/w/index.php?title=Tri%C3%A1ngulo_de_Kepler&printable=yes
, o aproximadamente 1 : 1,272 : 1,618.3 Los cuadrados de los lados de éste triángulo (véase fig. tk1) están en progresión geométrica de acuerdo al número áureo.- ........................................................................:https://es.wikipedia.org/w/index.php?title=Tri%C3%A1ngulo_de_Kepler&printable=yes
Triángulo de Reuleaux
El triángulo Reuleaux es el ejemplo más sencillo de los llamados polígonos de Reuleaux, denominados así por el científico e ingeniero que los desarrolló, Franz Reuleaux. Estos polígonos tienen la particularidad de ser curvas de anchura constante, es decir, que la distancia entre dosrectas tangentes paralelas opuestas es la misma, independientemente de la dirección de esas rectas. Esto puede apreciarse en la figura adjunta, en la que siempre hay cuatro puntos de tangencia con el cuadrado, uno en cada lado.
El área del triángulo de Reuleaux es  , donde a es la anchura constante. El área de un círculo de igual diámetro es
, donde a es la anchura constante. El área de un círculo de igual diámetro es  , que es mayor. Más aún, el teorema de Blaschke-Lebesgue establece que el triángulo de Reuleaux tiene menor superficie que cualquier otra figura de igual anchura constante.
, que es mayor. Más aún, el teorema de Blaschke-Lebesgue establece que el triángulo de Reuleaux tiene menor superficie que cualquier otra figura de igual anchura constante.
 , donde a es la anchura constante. El área de un círculo de igual diámetro es
, donde a es la anchura constante. El área de un círculo de igual diámetro es  , que es mayor. Más aún, el teorema de Blaschke-Lebesgue establece que el triángulo de Reuleaux tiene menor superficie que cualquier otra figura de igual anchura constante.
, que es mayor. Más aún, el teorema de Blaschke-Lebesgue establece que el triángulo de Reuleaux tiene menor superficie que cualquier otra figura de igual anchura constante.
Su perímetro es  (véase la explicación en la sección siguiente).
(véase la explicación en la sección siguiente).
 (véase la explicación en la sección siguiente).
(véase la explicación en la sección siguiente).
El triángulo de Reuleaux puede generalizarse a otros polígonos regulares con un número impar de lados, como puede ser el caso de las monedas británicas de 20 peniques (basadas en un heptágono).
Partiendo de un triángulo equilátero de lado a delíniese, haciendo centro en uno de los vértices del triángulo y con radio a, un arco de circunferencias que una entre sí a los dos vértices restantes, repítase la operación para cada vértice y ya se habrá obtenido el triángulo de Reuleaux buscado. Borrando el triángulo inicial, el espacio central que delimitan en común las tres cirunferencias es el triángulo de Reuleaux, una curva de anchura constante.
Cada uno de los ángulos de un triángulo equilátero es de 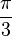 radianes. Cada uno de los tres arcos es de longitud
radianes. Cada uno de los tres arcos es de longitud  . Por tanto el perímetro del triángulo de Reuleaux es
. Por tanto el perímetro del triángulo de Reuleaux es  .
.
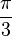 radianes. Cada uno de los tres arcos es de longitud
radianes. Cada uno de los tres arcos es de longitud  . Por tanto el perímetro del triángulo de Reuleaux es
. Por tanto el perímetro del triángulo de Reuleaux es  .
.- Debido a que todos sus diámetros tienen la misma longitud, el triángulo Reuleaux, junto con los demás polígonos regulares de Reuleaux, es la respuesta a la pregunta "Además de un círculo, ¿qué otra forma puede tener una tapa de alcantarilla para que no caiga a través del agujero?"
- El rotor de un Motor Wankel puede fácilmente ser confundido con un triángulo de Reuleaux. Aunque se parece mucho en su aspecto, el rotor Wankel tiene entre vértices una curva algo más plana que la del triángulo de Reuleux y por ello no tiene ancho constante.1
- En 1914 el ingeniero británico Harry James Watt patentó (US-Patent 1241175 y siguientes) una broca(llamada de Harry Watt en los países de habla inglesa) con forma de triángulo de Reuleaux. Esta broca va montada en un dispositivo especial que hace que gire un tanto excéntricamente y así puede taladrar un agujero con una forma casi exactamente cuadrada. En la figura se puede ver la rotación de esta broca dentro de un agujero cuadrado. Se ve que solo en las esquinas dicha broca deja cuatro pequeñas áreas sin cubrir, que suman un 1,33% del área del cuadrado.
- Un triángulo de Reuleaux puede rodar fácilmente, pero no funciona bien como rueda debido a que no tiene un centro fijo de rotación. Sin embargo, en la figura adjunta la tabla puede hacerse avanzar de manera perfctamente horizontal. En el rodillo de la izquierda habrá un eje que solo se desplace horizontalmente, mientras que en la sección del rodillo de la derecha, que es un triángulo de Reuleux, todos los puntos tienen algo de movimiento vertical, como se aprecia en la animación de la broca de Harry Watt.
- La existencia de los polígonos de Reuleaux es una buena demostración de que el que una figura tenga anchura constante no implica que sea un círculo.
- Muchos lápices son fabricados con este perfil, en lugar de los mucho más tradicionales de sección redonda o hexagonal.2 Por lo general son promocionados como más cómodos y producen un agarre adecuado, además de ser menos probable que rueden fuera las mesas.
Triángulo de Sierpinski
El triángulo de Sierpiński es un fractal que se puede construir a partir de cualquier triángulo.
Como en la mayoría de los fractales, existen varias maneras de obtener la misma figura (triángulos). En este caso, todos los procesos implican las tres homotecias centradas en los vértices del triángulo, de razón 1/2. Notémoslas ha, hb y hc.
Es fácil observar que ésta figura contiene tres reducciones de sí misma: El triángulo ADE con todo su contenido es una reducción exacta del triángulo ABC, y lo mismo se puede decir de CDF y de BEF. Estos tres clonos son justamente las imágenes de ABC por ha, hb y hc. Y como no quedan puntos del fractal fuera de éstas tres reducciones, se puede escribir (T designa el triángulo de Sierpiński):
Es fácil observar que ésta figura contiene tres reducciones de sí misma: El triángulo ADE con todo su contenido es una reducción exacta del triángulo ABC, y lo mismo se puede decir de CDF y de BEF. Estos tres clonos son justamente las imágenes de ABC por ha, hb y hc. Y como no quedan puntos del fractal fuera de éstas tres reducciones, se puede escribir (T designa el triángulo de Sierpiński):
En otras palabras, T es invariable por la aplicación del plano definida así: f(M) = {ha(M), hb(M), hc(M)}, donde M es un punto cualquiera del plano. Ésta aplicación es más abstracta de lo que parece pues su conjunto de llegada (codominio) no es el plano mismo sino las partes de él, o sea el conjunto de todas las figuras posibles del plano. Se puede extender el dominio de f a las partes del plano así: f(F) = ha(F) ∪ hb(F) ∪ hc(F) donde F es una figura cualquiera del plano.
Visto así, T es un punto fijo de f. El único, aparte del conjunto vacío, de escaso interés geométrico.
T es también un atractor de la aplicación f: si se considera una figura (de preferencia sencilla) T0, y se construyen su imágenes sucesivas T1 = f(T0), T2 = f(T1) = f 2(T0) ... Tn = f n(T0)... entonces la sucesión Tn se aproxima al triángulo de Sierpiński.
Visto así, T es un punto fijo de f. El único, aparte del conjunto vacío, de escaso interés geométrico.
T es también un atractor de la aplicación f: si se considera una figura (de preferencia sencilla) T0, y se construyen su imágenes sucesivas T1 = f(T0), T2 = f(T1) = f 2(T0) ... Tn = f n(T0)... entonces la sucesión Tn se aproxima al triángulo de Sierpiński.
En la figura siguiente se ha tomado como figura inicial el triángulo ABC:
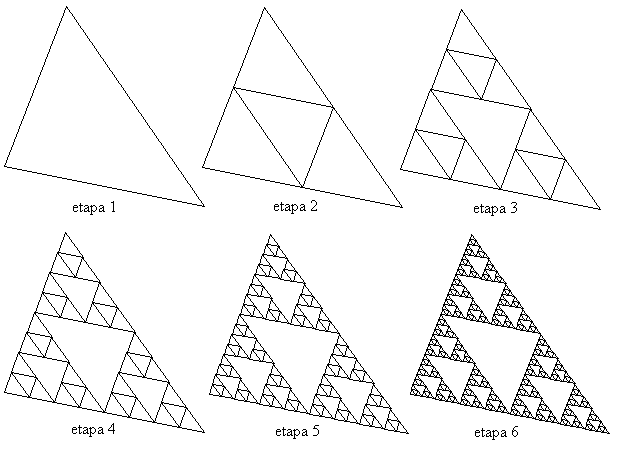
También se puede construir T a partir de un punto aleatorio cualquiera M y, para simplificar la programación, escoger al azar una imagen entre ha(M), hb(M) y hc(M) (en cada paso) en vez de tomar siempre las tres. Esto permite hacer un programa sin recursividad, pero claro, trae una desventaja: el número de pasos para obtener una figura satisfactoria será mucho más largo (en cada paso sólo se dibuja un punto):
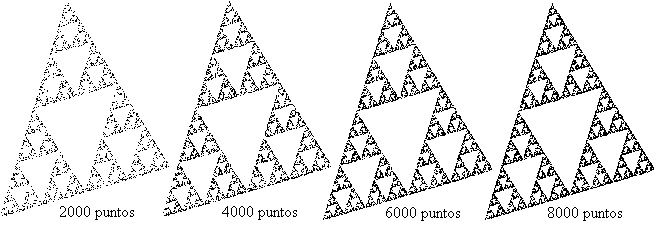
El triángulo de Sierpinski tiene una dimensión fractal de Hausdorff-Besicovitch coincidente con su dimensión fractal de homotecia igual a:
Igualmente fácil es encontrar la dimensión fractal usando un sistema iterativo de funciones, formado por tres funciones contractivas con constante de Lipschitz 1/2 de donde se sigue que la dimensión fractal de Hausdorff-Besicovitch satisface:





No hay comentarios:
Publicar un comentario