Teselación de Penrose
Una Teselación de Penrose o suelo de baldosas de Penrose es una teselación no periódica generada por un conjunto aperiódico de baldosas prototipo nombradas en honor aRoger Penrose, quien investigó esos conjuntos en la década de los 70. Debido a que todas las teselaciones obtenidas con las baldosas de Penrose son no periódicas, las teselaciones de Penrose han sido consideradas como teselaciones aperiódicas. Entre el infinito número de posibles teselaciones hay dos que poseen eje de simetría y una simetría rotacional de orden cinco, como en el diagrama mostrado a la derecha, y el término de Teselación de Penrose usualmente se refiere a esos.- .......................:https://es.wikipedia.org/w/index.php?title=Teselaci%C3%B3n_de_Penrose&printable=yes
Tetraedro de Reeve
En geometría, el tetraedro de Reeve (nombrado así en honor a John Reeve) es un poliedro enR3 cuyos vértices están ubicados en (0, 0, 0), (1, 0, 0), (0, 1, 0) y (1, 1, r) donde r es un entero positivo. Cada vértice es un punto en la retícula Z3. Ningún otro punto de esa retícula cae en la superficie o en el interior del tetraedro. En 1957, Reeve usó este tetraedro como contraejemplopara mostrar que no existe ningún equivalente del teorema de Pick en R3. Sin embargo, existe una generalización en dimensiones superiores mediante polinomios de Ehrhart.1 Esto se puede ver fijándose que el tetraedro de Reeve tiene el mismo número de puntos interiores y de borde para cualquier valor de r (cuatro puntos en los bordes y ninguno en el interior), pero su volumen varía. El volumen del tetraedro de Reeve es  .
.
 .
.Tetraedro de Reuleaux
El Tetraedro de Reuleaux es el cuerpo sólido resultante de la intersección de cuatro esferas de radio r, cuyos centros se encuentran en los vértices de un tetraedro regular de lado r. Al ser r el valor del radio de las esferas y el del tetraedro regular, cada una de las esferas contienen los vértices opuestos al vértice centro de las mismas. El tetraedro de Reuleaux cuenta con la misma estructura que un tetraedro regular, pero con las caras curvas. Esta forma volumétrica recibió el nombre por la analogía con el Triángulo de Reuleaux, forma bidimensional curva de longitud constante definida por Franz Reuleaux previamente.
Analizando el Triángulo de Reuleaux se observa que se trata de una figura curva de longitud constante, dado que es una forma planar convexa cuya longitud o anchura, medida por la distancia entre dos líneas paralelas tangentes a sus bordes, es la misma independientemente de la dirección de estas dos paralelas. De la misma manera que se puede hacer una extrapolación de 2D a 3D en la definición del tetraedro de Reuleaux, se podría considerar que este tetraedro cumple las características de una superficie de longitud constante. Sin embargo, esto no es cierto, ya que se alcanzan valores superiores al valor r en los puntos medios de las aristas adyacentes a los vértices de las esferas, de valor:
En 1912 por Meissner y Schiller, demostraron cómo modificar el tetraedro de Reuleaux para convertirlo en una superficie de longitud constante. El resultado de sus modificaciones son dos formas incongruentes que reciben el nombre de Tetraedros de Meissner, o Cuerpos de Meissner.
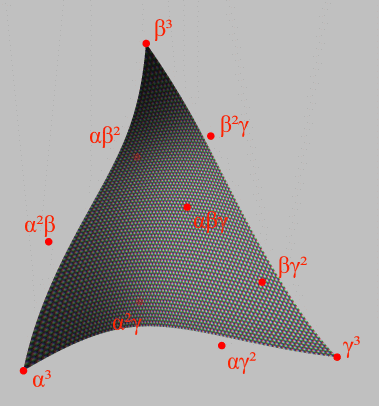
Un triángulo cúbico Bézier es una superficie con ecuación
Donde α3, β3, γ3, α2β, αβ2, β2γ, βγ2, αγ2, α2γ y αβγ son los puntos de control del triángulo.
Las esquinas del triángulo son los puntos α3, β3 y γ3. Los lados del triángulo son en sí curvas de Bézier con los mismos puntos de control que el triángulo de Bézier.
También es posible crear una función cuadrática o triángulos Bézier de grados superiores, cambiando el exponente en la ecuación original, en cuyo caso habrá más o menos puntos de control. Con exponente uno, el triángulo Béizer resultante es un triángulo convencional. En cualquier caso, los lados del triángulo serán curvas Béizer del mismo grado.







No hay comentarios:
Publicar un comentario