La curva de Hilbert (también conocida como la curva que recubre el plano de Hilbert) es una curva fractal continua que recubre el plano descrita inicialmente por el matemático alemán David Hilbert en 1891,1 como una variante de las curvas que recubren el plano descubiertas por Giuseppe Peano en 1890.2
Debido a que recubre el plano, su dimensión de Hausdorff-Besicovitch es  (precisamente, su imagen es el cuadrado unitario, cuya dimensión es 2 en cualquier definición de dimensión; su gráfico es un conjunto compacto homeomórfico al intervalo cerrado de la unidad, con una dimensión de Hausdorff de 2).
(precisamente, su imagen es el cuadrado unitario, cuya dimensión es 2 en cualquier definición de dimensión; su gráfico es un conjunto compacto homeomórfico al intervalo cerrado de la unidad, con una dimensión de Hausdorff de 2).
 (precisamente, su imagen es el cuadrado unitario, cuya dimensión es 2 en cualquier definición de dimensión; su gráfico es un conjunto compacto homeomórfico al intervalo cerrado de la unidad, con una dimensión de Hausdorff de 2).
(precisamente, su imagen es el cuadrado unitario, cuya dimensión es 2 en cualquier definición de dimensión; su gráfico es un conjunto compacto homeomórfico al intervalo cerrado de la unidad, con una dimensión de Hausdorff de 2).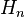 es la
es la  ésima aproximación al límite de la curva. La distancia euclidiana de
ésima aproximación al límite de la curva. La distancia euclidiana de 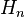 es
es  , i.e., crece exponencialmente con
, i.e., crece exponencialmente con  , a la vez que está siempre contenida en un cuadrado de área finita.- ................................................................:https://es.wikipedia.org/w/index.php?title=Curva_de_Hilbert&printable=yes
, a la vez que está siempre contenida en un cuadrado de área finita.- ................................................................:https://es.wikipedia.org/w/index.php?title=Curva_de_Hilbert&printable=yes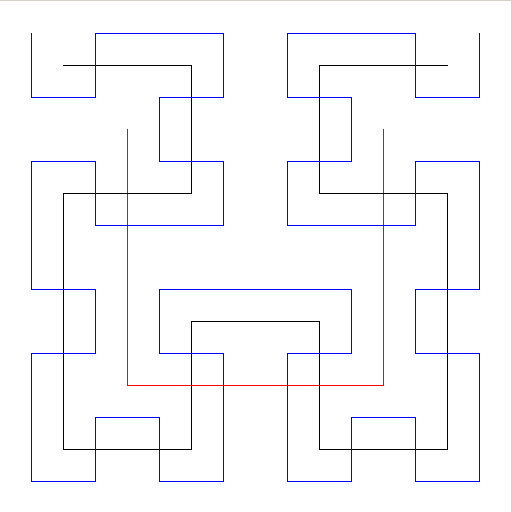



curva de Lévy C es un fractal autosimilar. Descrita por primera vez por Ernesto Cesàro en 19061 y G. Farber en 1910,2 hoy lleva el nombre del matemático francés Paul Pierre Lévy quien, en 1938, fue el primero en exhibir sus propiedades de autosimilaridad y proveer una construcción geométrica.
Utilizando un sistema de Lindenmayer, la construcción de la curva de Lévy C parte de un segmento de recta, este segmento se toma por la hipotenusa de un triángulo rectángulo isósceles, y se reemplaza por los dos catetos de dicho triángulo. De este modo, en esta etapa la curva consiste únicamente de dos segmentos de recta perpendiculares.
En la etapa siguiente, los dos segmentos son tomados como las hipotenusas de dos triángulos rectángulos isósceles, y se les reemplaza por los dos catetos correspondientes, y así sucesivamente.
Después de n etapas, la curva consistirá de 2n segmentos de recta, cada uno de longitud 2n/2 con respecto al segmento de partida.
El sistema de Lindenmayer asociado puede describirse entonces del siguiente modo:
En la etapa siguiente, los dos segmentos son tomados como las hipotenusas de dos triángulos rectángulos isósceles, y se les reemplaza por los dos catetos correspondientes, y así sucesivamente.
Después de n etapas, la curva consistirá de 2n segmentos de recta, cada uno de longitud 2n/2 con respecto al segmento de partida.
El sistema de Lindenmayer asociado puede describirse entonces del siguiente modo:
-
Variables: F Constantes: + − Inicio: F Reglas: F → +F−−F+
donde "F" significa "avanza recto", "+" significa "gira a la derecha 45°", y "−" significa "gira a la izquierda 45°". En el límite, el resultado de este proceso infinito es el fractal conocido como curva de Lévy C, dado su parecido con la letra C.
Variantes
Es posible construir variantes de esta curva utilizando ángulos diferentes de 45°, siempre y cuando sean menores a 60°.
Sistema IFS
La construcción de la curva de Lévy por medio de un sistema de funciones iteradasse basa en un conjunto de dos aplicaciones contractivas lineales de factor 1/√2. La primera introduce una rotación de 45°, y la segunda una rotación de -45°.


No hay comentarios:
Publicar un comentario