Curva de Peano
Una curva de Peano, nombre en honor al matemático italiano Giuseppe Peano, es un tipo de curva continua que "recubre" todo el plano (específicamente, la curva es un conjunto denso del plano). Este tipo de curvas se obtienen mediante una sucesión de curvas continuas sin intersecciones que convergen a una curva límite. La curva límite de o curva de Peano de hecho es un objeto fractal interesante, ya que aunque su dimensión topológica es 1 su dimensión fractalde Hausdorff-Besicovitch es 2.
Técnicamente la curva de Peano es el límite de una sucesión de curvas con las siguientes propiedades:
- Cada una de las curvas es continua y la sucesión converge uniformemente.
- Cada función es inyectiva, y es homeomorfa a un intervalo.
Esas dos propiedades implican que la curva límite satisfará las siguientes condiciones:
- Será una curva continua e sobreyectiva pero no inyectiva (aun cuando se obtenga como límite de curvas inyectivas).
- La curva de Peano es equipotente a la región [0; 1]x[0; 1]; sin embargo la dimensión de la curva peaniana es 1 y del cuadrado es 2.
La construcción puede generalizarse a cualquier dimensión n y pueden construirse curvas (con dimensión topológica 1) pero cuya dimensión de Hausdorff-Besicovitch iguala la del espacio. Esto último implica que la clausura topológica en el espacio euclídeo de dicha curva tiene un volumen n-dimensional diferente de cero.
Es la aplicación continua del intervalo unidad 0 ≤ t ≤ 1 sobre el cuadrado unidad Q : 0 ≤ 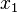 ≤ 1, 0 ≤
≤ 1, 0 ≤  ≤ 1 de
≤ 1 de 
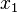 ≤ 1, 0 ≤
≤ 1, 0 ≤  ≤ 1 de
≤ 1 de 
- Los puntos en el intervalo unidad se consideran en el sistema de base 4.
Diagrama de Schlegel
En geometría, un diagrama de Schlegel es una proyección de un politopo contenido en  sobre el espacio
sobre el espacio  a través de un punto que está más allá de una de sus "caras". La entidad resultante es una división politópica de las caras en
a través de un punto que está más allá de una de sus "caras". La entidad resultante es una división politópica de las caras en  que es combinatoriamente equivalente al politopo original. En 1886 Victor Schlegel introdujo esta herramiento para estudiar propiedades combinatorias y topológicas de los politopos. En dimensiones, 3 y 4, un diagrama de Schlegel es una proyección de un poliedro sobre el plano dando una figura plana y una proyección de un polícoro al espacio tridimensional, respectivamente. Como tal, los diagramas de Schlegel se usan frecuentemente para visualizar politopos del espacio de cuatro dimensiones.
que es combinatoriamente equivalente al politopo original. En 1886 Victor Schlegel introdujo esta herramiento para estudiar propiedades combinatorias y topológicas de los politopos. En dimensiones, 3 y 4, un diagrama de Schlegel es una proyección de un poliedro sobre el plano dando una figura plana y una proyección de un polícoro al espacio tridimensional, respectivamente. Como tal, los diagramas de Schlegel se usan frecuentemente para visualizar politopos del espacio de cuatro dimensiones.
 sobre el espacio
sobre el espacio  a través de un punto que está más allá de una de sus "caras". La entidad resultante es una división politópica de las caras en
a través de un punto que está más allá de una de sus "caras". La entidad resultante es una división politópica de las caras en  que es combinatoriamente equivalente al politopo original. En 1886 Victor Schlegel introdujo esta herramiento para estudiar propiedades combinatorias y topológicas de los politopos. En dimensiones, 3 y 4, un diagrama de Schlegel es una proyección de un poliedro sobre el plano dando una figura plana y una proyección de un polícoro al espacio tridimensional, respectivamente. Como tal, los diagramas de Schlegel se usan frecuentemente para visualizar politopos del espacio de cuatro dimensiones.
que es combinatoriamente equivalente al politopo original. En 1886 Victor Schlegel introdujo esta herramiento para estudiar propiedades combinatorias y topológicas de los politopos. En dimensiones, 3 y 4, un diagrama de Schlegel es una proyección de un poliedro sobre el plano dando una figura plana y una proyección de un polícoro al espacio tridimensional, respectivamente. Como tal, los diagramas de Schlegel se usan frecuentemente para visualizar politopos del espacio de cuatro dimensiones.

esfera consciente de Alexander es una 2-esfera embebida en R3, cuyo exterior no es homeomorfo al exterior de la 2-esfera canónica en R3.
Fue descubierta en 1924 por el matemático James Alexander como un ejemplo patológico que mostraba la imposibilidad de generalizar el Teorema de la curva de Jordan-Schönflies a dimensiones superiores.
Descrita de modo informal, se construye, como muestra la figura, sacando dos "cuernos" a una esfera, aproximándolos, dividiendo en dos cada uno de los cuernos anteriores y volviéndolos a aproximar, repitiendo el proceso indefinidamente.
Representa un objeto topológicamente equivalente a la 2-esfera canónica de R3, pero embebido en R3 de forma muy diferente. Si nos fijamos en el exterior de la esfera cornuda de Alexander, encontraremos que la esfera se encuentra anudada. En una esfera canónica siempre podremos liberar una cuerda atada en su exterior, pero en la esfera cornuda de Alexander será imposible liberar una cuerda que tenga que pasar a través de los cuernos entrelazados.
Así, del mismo modo que todos los nudos como espacios topológicos son homeomorfos a una circunferencia, pero nudos no equivalentes pueden tener exteriores no homeomorfos, la esfera canónica de R3 y la esfera cornuda de Alexander son homeomorfas y sus exteriores no.



No hay comentarios:
Publicar un comentario