copo de nieve de Koch, también llamado estrella de Koch, es una curva cerrada continua pero no diferenciable en ningún punto descrita por el matemático sueco Helge von Koch en 1904 en un artículo titulado "Acerca de una curva continua que no posee tangentes y obtenida por los métodos de la geometría elemental".1 2
En lenguaje actual, diríamos que es una curva fractal. Su construcción más simple se realiza mediante un proceso iterativo que se inicia partiendo en tres un segmento de recta e insertando dos más en el tercero medio a manera de un triángulo equilátero, el proceso se repite infinidad de veces. La curva de Koch es un caso particular de curva de De Rham.- ..................................:https://es.wikipedia.org/w/index.php?title=Copo_de_nieve_de_Koch&printable=yes




Poliedro de Császár
| Császár polyhedron | |
|---|---|
| Tipo | Poliedro toroidal |
| Caras | 14 triángulos |
| Aristas | 21 |
| Vértices | 7 |
| Característica de Euler | 0 |
| Género | 1 |
| Configuración de vértices | 3.3.3.3.3.3 |
| Grupo de simetría | C2 |
| Dual | Poliedro de Szilassi |
| Propiedades | No convexo |
En geometría, el Poliedro de Császár (ˈtʃaːsaːr) es un poliedro no convexo, topológicamente un toro, con 14 caras triangulares.
Este poliedro no tiene diagonales; cada par de vértices están conectados por una arista. Los 7 vértices y 21 aristas del poliedro forma el grafo completo 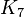 sobre la superficie de un toro.
sobre la superficie de un toro.
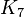 sobre la superficie de un toro.
sobre la superficie de un toro.
El tetraedro y el poliedro de Császár son los únicos poliedros conocidos que no tienen diagonales, aunque hay otros poliedros conocidos tales como el poliedro de Schönhardt que no tienen diagonales interiores (es decir, todas las diagonales están en el exterior del poliedro), así como las superficies de una sola cara sin diagonales. Si un poliedro con v vértices es proyectado sobre una superficie con h agujeros, de alguna manera cada par de vértices se conecta por una arista, y se deduce de su característica de Euler que
Esta ecuación se satisface para el tetraedro con h = 0 y v = 4, y para el poliedro de Császar con h =1 y v =7. La próxima posible solución, h = 6 y v = 12, correspondería a un poliedro con 44 caras y 66 aristas, pero no es realizable como un poliedro; no se conoce si tal poliedro existe con un género mayor. De manera general, esta ecuación se puede satisfacer sólo cuando v es congruente con 0, 3, 4, ó 7 módulo 12.
El poliedro de Császár recibe su nombre por el topólogo Ákos Császár, quien lo descubrió en 1949. Su poliedro dual es el poliedro de Szilassi, que fue descubierto más tarde, en 1977, por Lajos Szilassi; éste tiene 14 vértices, 21 aristas, y 7 caras hexagonales, cada una comparte una arista con cada una de las otras caras. Al igual que el poliedro de Császár, el poliedro de Szilassi es topológicamente equivalente a un toro.



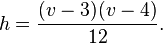
No hay comentarios:
Publicar un comentario