Teorema de Abel-Ruffini
teorema de Abel o teorema de Abel-Ruffini postula que no pueden resolverse por radicales las ecuaciones polinómicas generales de grado igual o superior a cinco.
Es decir, no es posible encontrar las soluciones de la ecuación general:
de grado superior o igual a cinco, aplicando únicamente un número finito de sumas, restas, multiplicaciones, divisiones y extracción de raíces a los coeficientes de la ecuación.
El contenido de este problema es generalmente mal entendido:
- El teorema no afirma que las ecuaciones polinómicas de grado cinco o superior no tengan soluciones o que no puedan ser resueltas. De hecho, si la ecuación polinómica tiene coeficientes reales o complejos y permitimos soluciones complejas, entonces cualquier ecuación polinomial tiene soluciones; éste es el teorema fundamental del álgebra. Aunque estas soluciones no siempre pueden ser calculadas exactamente con un número finito de operaciones aritméticas, pueden serlo hasta cualquier grado de exactitud deseado usando métodos numéricos tales como el método de Newton-Raphson o el Método de Laguerre, y de ese modo no son diferentes de las soluciones de las ecuaciones polinómicas de segundo, tercero y cuarto grados.
- El teorema solo se refiere a la forma que una solución debe tomar. El contenido del teorema es que la solución de una ecuación de grado cinco o superior no puede siempre ser expresada comenzando por los coeficientes y usando solo finitamente las operaciones de suma, multiplicación,y radicación.
- El teorema es falso para ecuaciones de grados inferiores a cinco. Por ejemplo, las soluciones de la ecuación de segundo gradoax2 + bx + c = 0 pueden ser expresadas en términos de adición, multiplicación y extracción de raíces como:

- Formas análogas para las ecuaciones polinómicas de tercer y cuarto grado, usando raíces cúbicas y cuartas, han sido conocidas desde el siglo XVI.
- Para grados superiores o iguales a cinco, el teorema especifica que no puede resolverse por radicales cualquier ecuación pero hay ecuaciones particulares que sí pueden resolverse por radicales. Así, el teorema de Saüch-Ruffini dice que hay algunas ecuaciones de quinto grado cuya solución no puede ser expresada de ese modo como por ejemplo la ecuación x5 - x + 1 = 0. Sin embargo, algunas otras ecuaciones de quinto grado pueden ser resueltas mediante radicales, por ejemplo x5 - x4 - x + 1 = 0.
- El criterio preciso que separa aquellas ecuaciones que pueden ser resueltas mediante radicales de aquellas que no fue dado porÉvariste Galois y es parte de la Teoría de Galois: una ecuación polinómica puede ser resuelta mediante radicales si y sólo si sugrupo de Galois es un grupo resoluble. En el análisis moderno, la razón por la que las ecuaciones polinomiales de segundo, tercero y cuarto grado pueden ser resueltas mediante radicales mientras que las ecuaciones de grado superior no, es simplemente el hecho algebraico de que los grupos simétricos S2, S3 y S4 son grupos resolubles, mientras que Sn no es resoluble para n ≥ 5.
La siguiente demostración está basada en la Teoría de Galois. Uno de los teoremas fundamentales de la teoría de Galois dice que una ecuación se puede resolver en radicales si, y solo si tiene un Grupo de Galois que se puede resolver, entonces la demostración del teorema de Abel-Ruffini viene de calcular el grupo de Galois del polinomio general de quinto grado.
Sea 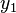 un número real trascendente sobre el cuerpo de los números racionales
un número real trascendente sobre el cuerpo de los números racionales 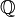 , y sea
, y sea  un número real trascendental sobre
un número real trascendental sobre  , y así hasta
, y así hasta  que es trascendental sobre
que es trascendental sobre  . Estos números son llamados elementos trascendentales independientes sobre
. Estos números son llamados elementos trascendentales independientes sobre 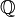 . Sea
. Sea  y sea
y sea
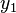 un número real trascendente sobre el cuerpo de los números racionales
un número real trascendente sobre el cuerpo de los números racionales 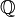 , y sea
, y sea  un número real trascendental sobre
un número real trascendental sobre  , y así hasta
, y así hasta  que es trascendental sobre
que es trascendental sobre  . Estos números son llamados elementos trascendentales independientes sobre
. Estos números son llamados elementos trascendentales independientes sobre 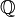 . Sea
. Sea  y sea
y sea![f(x) = (x - y_1)(x - y_2)(x - y_3)(x - y_4)(x - y_5) \in E[x].](https://upload.wikimedia.org/math/1/e/f/1ef26529bac4c8585abee214d9b26664.png)
- El método o regla de Ruffini es un método que nos permite dividir un polinomio entre un binomio y además permite localizar las raíces de un polinomio para factor izarlo en binomios. En otras palabras esta técnica posibilita dividir o descomponer un polinomio algebraico de grado n, en un binomio algebraico, y luego en otro polinomio algebraico de grado n-1. Y para que esto sea posible se necesita saber o conocer por lo menos una de las raíces del polinomio único, con el propósito de que la separación sea exacta.En el mundo matemático, a regla de Ruffini es una técnica eficaz para dividir un polinomio por un binomio de la forma x – r. La regla de Ruffini es un caso especial de la división sintética cuando el divisor es un factor lineal. El método de Ruffini fue descrito por el matemático, profesor y médico italiano Paolo Ruffini en el año de 1804, quien además de inventar el famoso método denominado regla de Ruffini, que ayuda a encontrar los coeficientes del resultado de la fragmentación de un polinomio por el binomio; también descubrió y formulo esta técnica sobre el cálculo aproximado de las raíces de las ecuaciones.Años más tarde, exactamente en 1819 y luego en 1845, fue abordado nuevamente este método por William George Horner, profesor y matemático inglés, quien indago sobre los estudios realizados por el italiano Paolo Ruffini y sus trabajos sobre esta técnica utilizada hoy en día. Posteriormente el método del matemático ingles fue utilizado por los matemáticos J.R. Young y De Morgan este último nacido en la india.
- teorema de Ado afirma que toda álgebra de Lie L de dimensión finita sobre un cuerpo K de característica ceropuede ser visto como un álgebra de Lie de matrices cuadradas con la operación del conmutador de matrices. Más exactamente, el teorema afirma que L admite una representación ρ sobre K, en un espacio vectorial de dimensión finita V, que es una representación fiel, por la que el álgebra L es isomorfa al conjunto de endomorfismos de V.Mientras que para álgebras de Lie asociadas a los grupos clásicos no hay nada nuevo en esta afirmación, en el caso general se obtiene un resultado con mayores consecuencias. Aplicado al álgebra de Lie real de un grupo de Lie G, el teorema no implica que G admite una representación fiel (lo cual no es cierto en general), sin más bien que G siempre tiene una representación lineal que es un isomorfismo local con un grupo lineal. Este resultado fue demostrado en 1935 por Igor Dmitrievich Ado de la Universidad Estatal de Kazán, que era un estudiante de Nikolai Chebotaryov.La restricción sobre la característica, fue suprimida más tarde por Kenkichi Iwasawa y Harish-Chandra (véase en las referencias Gerhard Hochschild para esta demostración más general).



No hay comentarios:
Publicar un comentario