teorema de Wedderburn-Artin establece que un anillo semisimple A es isomorfo a un producto de  anillos de matrices de orden
anillos de matrices de orden 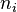 sobre anillos de división
sobre anillos de división  donde
donde  ,
, 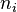 y
y  están determinados de forma única salvo el orden
están determinados de forma única salvo el orden  . Como consecuencia se obtiene que cualquier anillo simple y artiniano por la izquierda (o por la derecha) es isomorfo a un anillo de matrices de orden n sobre un anillo de división.
. Como consecuencia se obtiene que cualquier anillo simple y artiniano por la izquierda (o por la derecha) es isomorfo a un anillo de matrices de orden n sobre un anillo de división.
 anillos de matrices de orden
anillos de matrices de orden 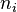 sobre anillos de división
sobre anillos de división  donde
donde  ,
, 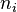 y
y  están determinados de forma única salvo el orden
están determinados de forma única salvo el orden  . Como consecuencia se obtiene que cualquier anillo simple y artiniano por la izquierda (o por la derecha) es isomorfo a un anillo de matrices de orden n sobre un anillo de división.
. Como consecuencia se obtiene que cualquier anillo simple y artiniano por la izquierda (o por la derecha) es isomorfo a un anillo de matrices de orden n sobre un anillo de división.
El teorema de Wedderburn-Artin reduce el problema de clasificar anillos simples sobre un anillo de división a clasificar anillos de división que contienen un anillo de división dado. Y esto todavía puede simplificarse más: el centro de un anillo de división será un cuerpo K. Por lo tanto, A es una K-álgebra que tiene a K como centro. Así, un álgebra simple de dimensión finita es un álgebra simple central sobre K. Consecuentemente, el teorema de Wedderburn-Artin reduce el problema de clasificar las álgebras simples centrales de dimensión-finita al problema de clasificar anillos de división con un centro dado de antemano.Sea  el cuerpo de los números reales,
el cuerpo de los números reales,  el de los números complejos, y
el de los números complejos, y  el anillo de división de los cuaterniones.
el anillo de división de los cuaterniones.
 el cuerpo de los números reales,
el cuerpo de los números reales,  el de los números complejos, y
el de los números complejos, y  el anillo de división de los cuaterniones.
el anillo de división de los cuaterniones.- Toda álgebra simple de dimensión finita sobre
 es un anillo de matrices sobre
es un anillo de matrices sobre  ,
,  o
o  .
. - Toda álgebra simple de dimensión finita sobre
 es un anillo de matrices sobre
es un anillo de matrices sobre  y por tanto, cada álgebra central simple sobre
y por tanto, cada álgebra central simple sobre  es un anillo de matrices sobre
es un anillo de matrices sobre  .
. - Toda álgebra central simple de dimensión finita sobre un cuerpo finito es un anillo de matrices sobre ese cuerpo.
No debe confundirse con el pequeño teorema de Wedderburn.
En matemáticas y especialmente en álgebra teorema de ofertas de Artin-Wedderburn con la estructura de álgebra o anillo semi-simple.
Se corresponde con el teorema fundamental de las estructuras semi-simple y permite explicar exactamente su naturaleza. Corresponden a algebraicas módulos de productos endomorfismos en campos no necesariamente conmutativa.
Se demuestra por primera vez como parte de álgebra sobre un campo en 1907 por Joseph Wedderburn entonces generalizada por Emil Artin en los anillos de encontrar su forma definitiva en 1927.
Este teorema se encuentra en el corazón de varias teorías incluyen representaciones de un grupo finito o no, la teoría de anillos que permite, por ejemplo para construir el cuerpo no conmutativa y también el de las estructuras semi-simples en general.
Adelante
Este teorema ha tenido varias versiones de su historia, aquí están los tres mejores:
La primera versión corresponde con el teorema de Burnside, que sólo trata con el caso de un álgebra simple:
Este segundo teorema corresponde, en términos corrientes en Wedderburn teorema, se trata de álgebra sobre un campo:
La tercera versión se expresa en términos de anillo que ahora lleva el nombre de Teorema de Artin-Wedderburn:
Los organismos en cuestión aquí son, a priori, dejó el cuerpo, es decir, no conmutativa.
El artículo sobre la semi-álgebra simple muestra que la versión Artin generaliza inmediatamente al álgebra.
Demostraciones
Definiciones
A lo largo de esta sección, se utilizan las siguientes anotaciones: K es un cuerpo conmutativo, L un álgebra sobre K y E un espacio vectorial sobre K. Varias definiciones se utilizan para expresar el teorema.
El álgebra L es también un módulo sobre el anillo L. Su submódulos L ya no tienen el concepto de dimensión porque la estructura de espacio vectorial está ausente de este ángulo. Se sustituye por la siguiente definición:
Se supone aquí que la L como módulo de L es semi-simple, que corresponde a la siguiente definición:
L funciona como derecha e izquierda en el módulo, un sub-módulo es un ideal de dos caras.
Tal álgebra es semi-simple. Estructura, como un módulo es conocido:
Aquí se refiere a una familia máxima en el sentido del inclustion de pares submódulos no isomorfos yai y el número de copias de Si en su componente de isotipo. Con las siguientes definiciones:
Durante todo el apartado relativo a manifestaciones, componentes isotípicos se denotan Si, el número n, el grado de multiplicidad yai, y Di marca lejos del cuerpo de endomorfismos de Si como módulo de L. Recordamos la siguiente definición:
Burnside Demostración
Sea f una endomorphism distinto de cero. Demostrar que el ideal de dos caras más pequeña que contiene f es todo el álgebra. f es distinto de cero, hay un elemento de E, E1 no pertenece al núcleo de f. Nota tiene e1 imagen por f. Complementar E1 E. básica para todos i y j variando desde 1 hasta n, pj observo el mapeo cero lineal basada en ej excepto que para la trama E1, y el qi es una aplicación lineal de tal manera que la imagen de a es igual a la IE. Así que la familia de qi ofo pj está incluido en el ideal generado por f. Además, esta familia genera L, que completa la demostración.
Esta demostración se extiende también al caso de los módulos en un cuerpo izquierdo. Este caso es importante porque, en el caso de semi-álgebra simple, establece el teorema de reciprocidad de Artin-Wedderburn.
Demostración de Artin
El teorema de Wedderburn es claramente un caso especial de la Artin. La demostración de Artin relativamente simple, sólo se da en este artículo.
Nota: hablar sobre el tamaño de un módulo tiene sentido aquí porque el módulo tiene que llamar al cuerpo. Esta estructura, sin embargo, no es la de un espacio vectorial, porque el cuerpo es a priori izquierda.
Probar primero el siguiente lema:
Es evidente que la suma directa se incluye en todos los L-endomorfismos
Por el contrario, el párrafo canónica Descomposición de módulo artículo semisimple muestra que sencilla submódulo del componente isotípico es isomorfo a Si Si. Schur lema asegura que no hay morfismo que no sea el morfismo anular entre dos módulos simples no isomorfos. Por lo tanto el único morfismo entre el componente isotípica de Si y Sj si i y j son diferentes son morfismos cero, lo que completa la demostración de este lema.
Luego probar el siguiente lema:
El razonamiento es similar a la del lema anterior. Si Sij para j variando de 1 a yai denota una suma descomposición directa del componente isotípico de Si, a continuación, cada factor Sij es isomorfo a Si. Todo el endormorphismes componente isoptypique es isomorfo al conjunto de matrices coeficientes en todos los módulos de endomorfismo Si. El conjunto de coeficientes es un cuerpo que es opuesta Di. El isomorfismo canónico entre el conjunto de matrices cuadradas de yai dimensión y todas endomorfismos de un espacio vectorial de dimensión yai completa la demostración de la segunda lema.
teorema de Arzelà-Ascoli es una de las herramientas más poderosas que hay para verificar si una familia de funciones de un espacio topólogico en otro es compacta. Lo que dice el teorema es lo siguiente:
Sea  un espacio topológico compacto,
un espacio topológico compacto,  un espacio métrico completo. Un conjunto
un espacio métrico completo. Un conjunto  (el espacio de las funciones continuas de
(el espacio de las funciones continuas de  en
en  ) será relativamente compacto en la topología de la métrica infinito si y solamente si:
) será relativamente compacto en la topología de la métrica infinito si y solamente si:
 un espacio topológico compacto,
un espacio topológico compacto,  un espacio métrico completo. Un conjunto
un espacio métrico completo. Un conjunto  (el espacio de las funciones continuas de
(el espacio de las funciones continuas de  en
en  ) será relativamente compacto en la topología de la métrica infinito si y solamente si:
) será relativamente compacto en la topología de la métrica infinito si y solamente si: es equicontinuo
es equicontinuo- Para todo
 , el conjunto
, el conjunto  es relativamente compacto en
es relativamente compacto en  .
.
Notar que si  , la condición 2 es equivalente a pedir que para cada
, la condición 2 es equivalente a pedir que para cada  , el conjunto
, el conjunto  sea acotado. En este mismo caso, se cumple que si además
sea acotado. En este mismo caso, se cumple que si además  es un espacio topólogico conexo, basta verificar que existe un
es un espacio topólogico conexo, basta verificar que existe un  tal que la condición 2 se cumple, y automáticamente se tendrá para todos.
tal que la condición 2 se cumple, y automáticamente se tendrá para todos.
 , la condición 2 es equivalente a pedir que para cada
, la condición 2 es equivalente a pedir que para cada  , el conjunto
, el conjunto  sea acotado. En este mismo caso, se cumple que si además
sea acotado. En este mismo caso, se cumple que si además  es un espacio topólogico conexo, basta verificar que existe un
es un espacio topólogico conexo, basta verificar que existe un  tal que la condición 2 se cumple, y automáticamente se tendrá para todos.
tal que la condición 2 se cumple, y automáticamente se tendrá para todos.
ejercicios de dicho teorema .- ..............:https://vargasmat.files.wordpress.com/2011/05/teorema-de-arsela-ascoli.pdf
teorema de Aumann sobre acuerdos establece que dos personas actuando racionalmente (en cierto sentido específico) y con unconocimiento común de las creencias del otro, no pueden acordar estar en desacuerdo. De manera más específica: si dos personas sonracionalistas bayesianos genuinos con distribuciones de probabilidad a priori comunes y si cada uno de ellos tiene conocimiento común de sus distribuciones de probabilidad a posteriori, entonces sus probabilidades posteriores deben ser iguales1
Surge la pregunta si dicho acuerdo se puede alcanzar en un tempo razonable y, desde la perspectiva matemática, si puede hacerse de forma eficiente. Scott Aaronson publicó un artículo en 2005 demostrando que la respuesta es afirmativa.2
Ciertamente, la suposición de los prioris comunes es muy fuerte y difícilmente se cumple en la práctica. Sin embargo Robin Hanson ha presentado un argumento planteando que los bayesianos que concuerden en los procesos que dan origen a sus prioris (por ejemplo, influencias en el ambiente o genética) deberían, si se adhieren a cierta condición de pre-racoinalidad, tener priores comunes.
No hay comentarios:
Publicar un comentario