AMIGOS PARA SIEMPRE: Matemáticas

Las matrices de Gell-Mann, que toman su nombre de Murray Gell-Mann, son una posible representación de los generadores infinitesimales del grupo unitario especial SU(3). El álgebra de Lie de este grupo (una álgebra de Lie real, de hecho) tiene dimensión ocho y por lo tanto un conjunto con ocho generadores linealmente independientes, que se pueden escribir como

g_i

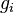con itomando valores entre 1 y 8.

Definición

Estos elementos del álgebra de Lie obedecen las relaciones de conmutación

[g_i, g_j] = if^{ijk} g_k \,

donde la suma sobre el índice k está implícita. Las constantes de estructura

f^{ijk}

son completamente antisimétricas en los tres índices y tiene valores

f^{123} = 1 \ , \quad f^{147} = f^{165} = f^{246} = f^{257} = f^{345} = f^{376} = \frac{1}{2} \ , \quad f^{458} = f^{678} = \frac{\sqrt{3}}{2} \ .

Cualquier conjunto de matrices Hermitianas que obedezca estas relaciones es válida. Una elección particular de matrices se llama una representación de grupo, porque cualquier elemento de SU(3) se puede escribir en la forma

\mathrm{exp}(i \theta_j g_j)

, donde

\theta_j

son números reales y la suma sobre el índice j está implícita. Dada una representación, otra puede ser obtenido mediante una transformación unitaria arbitraria, ya que no modifica el conmutador.

Representaciones particulares

Una representación importante involucra matrices 3×3 matrices porque los elementos del grupo operan sobre vectores complejos de 3 entradas, esto es, en la representación fundamental del grupo. Una elección particular de esta representación es

$\lambda_1 = \begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}$	$\lambda_2 = \begin{pmatrix} 0 & -i & 0 \\ i & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}$	$\lambda_3 = \begin{pmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 0 \end{pmatrix}$
$\lambda_4 = \begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \end{pmatrix}$	$\lambda_5 = \begin{pmatrix} 0 & 0 & -i \\ 0 & 0 & 0 \\ i & 0 & 0 \end{pmatrix}$
$\lambda_6 = \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{pmatrix}$	$\lambda_7 = \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & -i \\ 0 & i & 0 \end{pmatrix}$	$\lambda_8 = \frac{1}{\sqrt{3}} \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -2 \end{pmatrix}$

g_i = \lambda_i/2

Estas matrices tienen traza nula, son hermitianas, y obedecen la relación de normalización

\mathrm{tr}(\lambda_i \lambda_j) = 2\delta_{ij}

. Gell-Mann escogió estas propiedades para generalizar lasmatrices de Pauli para SU(2). También se pueden extender naturalmente a grupos generales SU(n).

En esta representación, es evidente que la subálgebra de Cartan es el conjunto de combinaciones lineales (con coeficientes reales) de las dos matrices

\lambda_3

\lambda_8

, que conmutan entre sí. Hay 3 subgrupos SU(2) independientes:

\{\lambda_1, \lambda_2, \lambda_3\}

\{\lambda_4, \lambda_5, x\}

\{\lambda_6, \lambda_7, y\}

, donde x e y son combinaciones lineales de

\lambda_3

\lambda_8

La suma cuadrada de las matrices de Gell-Mann da el operador cuadrático de Casimir, un invariante del grupo,

C = \sum_{i=1}^8 \lambda_i \lambda_i = 16/3

Además, hay otro operador de Casimir independiente, en este caso cúbico.

Estas matrices sirven para estudiar las rotaciones internas entre los diferentes colores de quarks en cromodinámica cuántica.

Definición

Estos elementos del álgebra de Lie obedecen las relaciones de conmutación

[g_i, g_j] = if^{ijk} g_k \,

donde la suma sobre el índice k está implícita. Las constantes de estructura

f^{ijk}

son completamente antisimétricas en los tres índices y tiene valores

f^{123} = 1 \ , \quad f^{147} = f^{165} = f^{246} = f^{257} = f^{345} = f^{376} = \frac{1}{2} \ , \quad f^{458} = f^{678} = \frac{\sqrt{3}}{2} \ .

\mathrm{exp}(i \theta_j g_j)

, donde

\theta_j

Representaciones particulares

$\lambda_1 = \begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}$	$\lambda_2 = \begin{pmatrix} 0 & -i & 0 \\ i & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}$	$\lambda_3 = \begin{pmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 0 \end{pmatrix}$
$\lambda_4 = \begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \end{pmatrix}$	$\lambda_5 = \begin{pmatrix} 0 & 0 & -i \\ 0 & 0 & 0 \\ i & 0 & 0 \end{pmatrix}$
$\lambda_6 = \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{pmatrix}$	$\lambda_7 = \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & -i \\ 0 & i & 0 \end{pmatrix}$	$\lambda_8 = \frac{1}{\sqrt{3}} \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -2 \end{pmatrix}$

g_i = \lambda_i/2

Estas matrices tienen traza nula, son hermitianas, y obedecen la relación de normalización

\mathrm{tr}(\lambda_i \lambda_j) = 2\delta_{ij}

. Gell-Mann escogió estas propiedades para generalizar lasmatrices de Pauli para SU(2). También se pueden extender naturalmente a grupos generales SU(n).

En esta representación, es evidente que la subálgebra de Cartan es el conjunto de combinaciones lineales (con coeficientes reales) de las dos matrices

\lambda_3

\lambda_8

, que conmutan entre sí. Hay 3 subgrupos SU(2) independientes:

\{\lambda_1, \lambda_2, \lambda_3\}

\{\lambda_4, \lambda_5, x\}

\{\lambda_6, \lambda_7, y\}

, donde x e y son combinaciones lineales de

\lambda_3

\lambda_8

La suma cuadrada de las matrices de Gell-Mann da el operador cuadrático de Casimir, un invariante del grupo,

C = \sum_{i=1}^8 \lambda_i \lambda_i = 16/3

Además, hay otro operador de Casimir independiente, en este caso cúbico.

Estas matrices sirven para estudiar las rotaciones internas entre los diferentes colores de quarks en cromodinámica cuántica.

Los ocho matrices de Gell-Mann

son un ejemplo del conjunto de generadores del álgebra de Lie asociada al grupo unitario especial

. Explícitamente, estas matrices tienen la forma

			(1)
			(2)
			(3)
			(4)
			(5)
			(6)
			(7)
			(8)

Tenga en cuenta que las ocho matrices de Gell-Mann son traceless y hermitiana y satisfacen la relación

, donde

denota el delta de Kronecker . Por otra parte, en la notación anterior,

es simétrico para

, antisimétrico para

, y diagonal para

. Debido a estas propiedades, se puede acceder a las matrices de Gell-Mann como una generalización tridimensional de las matrices de Pauli , que (con ligeras modificaciones) generan el álgebra de Lie asociada a .

Estas matrices son especialmente importantes en las matemáticas y la física. Por ejemplo, estas matrices (y sus generalizaciones) son importantes en la teoría de Lie. Además, también juegan un papel importante en la física en la que se pueden considerar para modelar los ocho gluones que median las fuertes cromodinámica cuántica fuerza, un análogo de la Pauli matrices se adapta bien a las aplicaciones en el campo de la mecánica cuántica.

Las matrices de Gell-Mann generalizadas son las matrices que generan el álgebra de Lie asociada al grupo unitario especial , . Como su nombre sugiere, estas matrices tienen la intención de generalizar tanto en el estándar matrices de Gell-Mann , que generan el álgebra de Lie asociada a , así como las matrices de Pauli que generan el álgebra de Lie asociada a .

El algoritmo para la construcción de las matrices generalizadas Gell-Mann es como sigue. A lo largo de, dejar que

denotan la matriz con un 1 en la

entrada TH y 0 en otras partes. Esto permite definir tres colecciones de matrices. La primera colección es simétrica :

(1)

para

. La segunda colección es antisimétrica :

(2)

para

. La tercera colección es diagonal matriz diagonal:

(3)

para

Esto da un total de

(4)

generalizadas matrices de Gell-Mann, que coinciden exactamente la real dimensión del álgebra de Lie asociada a

Tenga en cuenta que la construcción puede ser reformulada usando sujetador - cado notación (Bertlmann y Krammer 2008) también. Además, se puede comprobar fácilmente que los casos de