En el área matemática de la teoría de grafos , un gráfico de intersección es un gráfico que representa el patrón de intersecciones de una familia de conjuntos . Cualquier gráfico puede representarse como un gráfico de intersección, pero algunas clases especiales importantes de gráficos pueden definirse por los tipos de conjuntos que se utilizan para formar una representación de intersección de ellos.
Para una visión general de la teoría de los gráficos de intersección y las clases especiales importantes de gráficos de intersección, ver McKee y McMorris (1999) .
Definición formal [ editar ]
Formalmente, un gráfico de intersección es un gráfico no dirigido formado a partir de una familia de conjuntos
- S i , i = 0, 1, 2, ...
creando un vértice v i para cada conjunto S i , y conectando dos vértices v i y v j por un borde siempre que los dos conjuntos correspondientes tengan una intersección no vacía, es decir,
- E ( G ) = {{ v i , v j } | S i ∩ S j ≠ ∅}.
Todos los gráficos son gráficos de intersección [ editar ]
Cualquier gráfico G no dirigido puede representarse como un gráfico de intersección: para cada vértice v i de G , forme un conjunto S i que consista en los bordes incidentes a v i ; entonces dos de estos conjuntos tienen una intersección no vacía si y solo si los vértices correspondientes comparten un borde. Erdős, Goodman y Pósa (1966) proporcionan una construcción que es más eficiente (es decir, requiere un menor número total de elementos en todos los conjuntos S i combinados) en el que el número total de elementos del conjunto es como máximo n 2 / 4 donde nes el número de vértices en el gráfico. Acreditan la observación de que todos los gráficos son gráficos de intersección a Szpilrajn-Marczewski (1945) , pero dicen ver también a Čulík (1964) . El número de intersección de un gráfico es el número mínimo total de elementos en cualquier representación de intersección del gráfico.
Clases de gráficos de intersección [ editar ]
Muchas familias de gráficos importantes pueden describirse como gráficos de intersección de tipos más restringidos de familias de conjuntos, por ejemplo, conjuntos derivados de algún tipo de configuración geométrica:
- Un gráfico de intervalo se define como el gráfico de intersección de intervalos en la línea real, o de subgráficos conectados de un gráfico de ruta .
- Un gráfico de indiferencia puede definirse como el gráfico de intersección de intervalos unitarios en la línea real
- Un gráfico de arco circular se define como el gráfico de intersección de arcos en un círculo .
- Un gráfico de polígono-círculo se define como la intersección de polígonos con esquinas en un círculo.
- Una caracterización de un gráfico cordal es como el gráfico de intersección de subgrafías conectadas de un árbol .
- Un gráfico trapezoidal se define como el gráfico de intersección de trapecios formados a partir de dos líneas paralelas. Son una generalización de la noción de gráfico de permutación , a su vez son un caso especial de la familia de los complementos de gráficos de comparabilidad conocidos como gráficos de cocomparabilidad.
- Un gráfico de unidad de disco se define como la gráfica de intersección de unidades de disco en el plano.
- Un gráfico circular es el gráfico de intersección de un conjunto de acordes de un círculo.
- El teorema de empaque circular indica que los gráficos planos son exactamente los gráficos de intersección de familias de discos cerrados en el plano delimitado por círculos no cruzados.
- La conjetura de Scheinerman (ahora un teorema) establece que cada gráfico plano también puede representarse como un gráfico de intersección de segmentos de línea en el plano. Sin embargo, los gráficos de intersección de segmentos de línea también pueden no ser planos, y el reconocimiento de los gráficos de intersección de segmentos de línea está completo para la teoría existencial de los reales ( Schaefer 2010 ).
- El gráfico lineal de un gráfico G se define como el gráfico de intersección de los bordes de G , donde representamos cada borde como el conjunto de sus dos puntos finales.
- Un gráfico de cadena es el gráfico de intersección de curvas en un plano .
- Un gráfico tiene una boxicidad k si es el gráfico de intersección de cuadros multidimensionales de dimensión k , pero no de una dimensión más pequeña.
- Un gráfico de camarilla es el gráfico de intersección de camarillas máximas de otro gráfico
- Un gráfico de bloques del árbol de camarillas es el gráfico de intersección de componentes biconéctados de otro gráfico
Scheinerman (1985) caracterizó las clases de intersección de gráficos , familias de gráficos finitos que pueden describirse como los gráficos de intersección de conjuntos extraídos de una familia de conjuntos dada. Es necesario y suficiente que la familia tenga las siguientes propiedades:
- Cada subgrafo inducido de un gráfico en la familia también debe estar en la familia.
- Cada gráfico formado a partir de un gráfico en la familia al reemplazar un vértice por una camarilla también debe pertenecer a la familia.
- Existe una secuencia infinita de gráficos en la familia, cada uno de los cuales es un subgráfico inducido del siguiente gráfico en la secuencia, con la propiedad de que cada gráfico de la familia es un subgráfico inducido de un gráfico en la secuencia.
Si las representaciones del gráfico de intersección tienen el requisito adicional de que diferentes vértices deben estar representados por diferentes conjuntos, entonces se puede omitir la propiedad de expansión de la camarilla.
Conceptos relacionados [ editar ]
Un análogo teórico de la orden a los gráficos de intersección son las órdenes de contención . De la misma manera que una representación de intersección de un gráfico etiqueta cada vértice con un conjunto de modo que los vértices sean adyacentes si y solo si sus conjuntos tienen una intersección no vacía, por lo que una representación de contención f de un poset etiqueta cada elemento con un conjunto para que x e y en el poset, x ≤ y si y solo si f ( x ) ⊆ f ( y ).
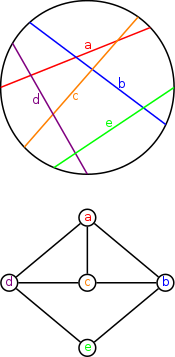
En la teoría de gráficos , un gráfico circular es el gráfico de intersección de un conjunto de acordes de un círculo . Es decir, es un gráfico no dirigido cuyos vértices pueden asociarse con los acordes de un círculo, de modo que dos vértices son adyacentes si y solo si los acordes correspondientes se cruzan entre sí.
Complejidad algorítmica [ editar ]
Spinrad (1994) proporciona un algoritmo de tiempo O ( n 2 ) que prueba si un gráfico no dirigido de n- vértices dado es un gráfico circular y, si lo es, construye un conjunto de acordes que lo representan.
Varios otros problemas que son NP-completos en gráficos generales tienen algoritmos de tiempo polinomiales cuando están restringidos a gráficos circulares. Por ejemplo, Kloks (1996) demostró que se puede determinar el ancho del árbol de un gráfico circular y construir una descomposición óptima del árbol en el tiempo O ( n 3 ). Además, se puede encontrar un relleno mínimo (es decir, un gráfico cordal con la menor cantidad de aristas posible que contenga el gráfico circular dado como un subgrafo) en el tiempo O ( n 3 ). [1] Tiskin (2010) ha demostrado que se puede encontrar una camarilla máxima de un gráfico circular en O ( n log 2 n), mientras que Nash y Gregg (2010) han demostrado que se puede encontrar un conjunto máximo independiente de un gráfico circular no ponderado en el tiempo O ( n min { d , α }), donde d es un parámetro del gráfico conocido como su densidad , y α es el número de independencia del gráfico circular.
Sin embargo, también hay problemas que siguen siendo NP completos cuando se restringen a gráficos circulares. Estos incluyen el conjunto dominante mínimo, el conjunto dominante mínimo conectado y los problemas de conjunto dominante mínimo total. [2]
Número cromático [ editar ]
El número cromático de un gráfico circular es el número mínimo de colores que se pueden usar para colorear sus acordes para que no haya dos acordes cruzados que tengan el mismo color. Como es posible formar gráficos circulares en los que conjuntos de acordes arbitrariamente grandes se cruzan entre sí, el número cromático de un gráfico circular puede ser arbitrariamente grande, y determinar el número cromático de un gráfico circular es NP-completo. [3] Sigue siendo NP-complete para probar si un gráfico circular puede ser coloreado por cuatro colores. [4] Unger (1992) afirmó que encontrar un color con tres colores puede hacerse en tiempo polinómico, pero su descripción de este resultado omite muchos detalles. [5]
Varios autores han investigado problemas para colorear subclases restringidas de gráficos circulares con pocos colores. En particular, para gráficos circulares en los que no se cruzan conjuntos de k o más acordes, es posible colorear el gráfico con tan solocolores. Una forma de afirmar esto es que los gráficos circulares son-limitado . [6] En el caso particular cuando k = 3 (es decir, para gráficos circulares sin triángulo ) el número cromático es como máximo cinco, y esto es apretado: todos los gráficos circulares sin triángulo pueden colorearse con cinco colores, y allí existen gráficos circulares sin triángulos que requieren cinco colores. [7] Si un gráfico circular tiene una circunferencia de al menos cinco (es decir, no tiene triángulos y no tiene ciclos de cuatro vértices), se puede colorear con un máximo de tres colores. [8] El problema de colorear cuadros cuadrados libres de triángulos es equivalente al problema de representar cuadros cuadrados como subgrafías isométricas de productos cartesianos de árboles; En esta correspondencia, el número de colores en el color corresponde al número de árboles en la representación del producto. [9]
Aplicaciones [ editar ]
Los gráficos circulares surgen en el diseño físico de VLSI como una representación abstracta de un caso especial para el enrutamiento de cables , conocido como " enrutamiento de caja de conmutación de dos terminales ". En este caso, el área de enrutamiento es un rectángulo, todas las redes son de dos terminales y los terminales se colocan en el perímetro del rectángulo. Se ve fácilmente que el gráfico de intersección de estas redes es un gráfico circular. [10] Entre los objetivos del paso de enrutamiento de cables se encuentra garantizar que las diferentes redes permanezcan desconectadas eléctricamente y que sus posibles partes de intersección se deben colocar en diferentes capas conductoras. Por lo tanto, los gráficos circulares capturan varios aspectos de este problema de enrutamiento.
Los colores de los gráficos circulares también se pueden usar para encontrar incrustaciones de libros de gráficos arbitrarios: si los vértices de un gráfico dado G están dispuestos en un círculo, con los bordes de G formando acordes del círculo, entonces el gráfico de intersección de estos acordes es un El gráfico circular y los colores de este gráfico circular son equivalentes a las incrustaciones de libros que respetan el diseño circular dado. En esta equivalencia, el número de colores en el color corresponde al número de páginas en la incrustación del libro. [4]
Clases gráficas relacionadas [ editar ]
Un gráfico es un gráfico circular si y solo si es el gráfico de superposición de un conjunto de intervalos en una línea. Este es un gráfico en el que los vértices corresponden a los intervalos, y dos vértices están conectados por un borde si los dos intervalos se superponen, sin que ninguno contenga al otro.
El gráfico de intersección de un conjunto de intervalos en una línea se llama gráfico de intervalos .
Los gráficos de cadenas , los gráficos de intersección de curvas en el plano, incluyen gráficos circulares como un caso especial.
Cada gráfico de distancia hereditaria es un gráfico circular, como lo es cada gráfico de permutación y cada gráfico de indiferencia . Cada gráfico del plano exterior también es un gráfico circular.




No hay comentarios:
Publicar un comentario