(Redirigido desde Garra (teoría de grafos) )
| Estrella | |
|---|---|
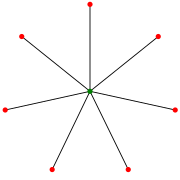
La estrella S 7 . (Algunos autores indexan esto como S 8 ).
| |
| Vértices | k + 1 |
| Bordes | k |
| Diámetro | mínimo de (2, k ) |
| Circunferencia | ∞ |
| Número cromático | mínimo de (2, k + 1) |
| Índice cromático | k |
| Propiedades | Distancia de unidad de árbol transitiva de borde Bipartita |
| Notación | S k |
| Tabla de gráficos y parámetros. | |
En la teoría de grafos , una estrella S k es el gráfico bipartito completo K 1, k : un árbol con un nodo interno y k se va (pero no hay nodos internos y k + 1 se va cuando k ≤ 1). Alternativamente, algunos autores definen S k como el árbol de orden k con diámetro máximo 2; en cuyo caso una estrella de k > 2 tiene k - 1 hojas.
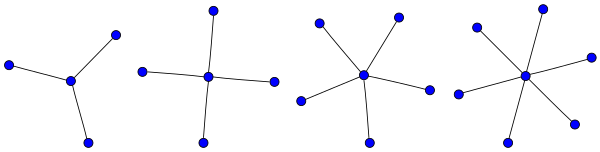
Una estrella con 3 aristas se llama garra .
La estrella S k es elegante cuando k es par y no cuando k es impar. Es un gráfico de fósforo con borde transitivo y tiene un diámetro 2 (cuando k > 1), circunferencia ∞ (no tiene ciclos), índice cromático k y número cromático 2 (cuando k > 0). Además, la estrella tiene un gran grupo de automorfismo, es decir, el grupo simétrico en k letras.
Las estrellas también pueden describirse como los únicos gráficos conectados en los que, como máximo, un vértice tiene un grado mayor que uno.
Relación con otras familias de gráficos [ editar ]
Las garras son notables en la definición de gráficos sin garras , gráficos que no tienen ninguna garra como un subgrafo inducido . [1] [2] También son uno de los casos excepcionales del teorema del isomorfismo del gráfico de Whitney : en general, los gráficos con gráficos de líneas isomorfas son en sí mismos isomorfos, con la excepción de la garra y el triángulo K 3 . [3]
Una estrella es un tipo especial de árbol . Como con cualquier árbol, las estrellas pueden estar codificadas por una secuencia de Prüfer ; La secuencia de Prüfer para una estrella K 1, k consiste en k - 1 copias del vértice central. [4]
Varios invariantes de grafos se definen en términos de estrellas. La arboricidad de la estrella es el número mínimo de bosques en los que se puede dividir un gráfico de manera que cada árbol en cada bosque sea una estrella, [5] y el número cromático de estrella de un gráfico es el número mínimo de colores necesarios para colorear sus vértices en tal una forma en que cada dos clases de color juntas forman una subgrafía en la que todos los componentes conectados son estrellas. [6] Los gráficos del ancho de rama 1 son exactamente los gráficos en los que cada componente conectado es una estrella. [7]
Otras aplicaciones [ editar ]
El conjunto de distancias entre los vértices de una garra proporciona un ejemplo de un espacio métrico finito que no puede incrustarse isométricamente en un espacio euclidiano de cualquier dimensión. [8]
La red estelar , una red informática modelada a partir del gráfico estelar, es importante en la informática distribuida .
Una realización geométrica del gráfico de estrella, formada mediante la identificación de los bordes con intervalos de cierta longitud fija, se utiliza como modelo local de curvas en geometría tropical . Una curva tropical se define como un espacio métrico que es localmente isomorfo a un gráfico métrico en forma de estrella.
En la teoría de grafos , un área de las matemáticas, un gráfico sin garras es un gráfico que no tiene una garra como un subgrafo inducido .
Una garra es otro nombre para el gráfico bipartito completo K 1,3 (es decir, un gráfico de estrella con tres bordes, tres hojas y un vértice central). Un gráfico sin garras es un gráfico en el que ninguna subgrafía inducida es una garra; es decir, cualquier subconjunto de cuatro vértices tiene otros tres bordes que los conectan en este patrón. De manera equivalente, un gráfico sin garras es un gráfico en el que la vecindad de cualquier vértice es el complemento de un gráfico sin triángulo .
Los gráficos sin garras se estudiaron inicialmente como una generalización de gráficos de líneas , y obtuvieron una motivación adicional a través de tres descubrimientos clave sobre ellos: el hecho de que todos los gráficos conectados sin garras de orden par tienen coincidencias perfectas , el descubrimiento de algoritmos de tiempo polinomiales para encontrar el máximo conjuntos independientes en gráficos sin garras y la caracterización de gráficos perfectos sin garras . [1] Son objeto de cientos de trabajos de investigación matemática y varias encuestas.
Ejemplos [ editar ]
- El gráfico lineal L ( G ) de cualquier gráfico G no tiene garras; L ( G ) tiene un vértice para cada borde de G , y vértices son adyacentes en L ( G ) siempre que los bordes correspondientes comparten un punto final en G . Un gráfico lineal L ( G ) no puede contener una garra, porque si tres aristas e 1 , e 2 y e 3 en G comparten puntos finales con otra arista e 4, entonces por el principio del casilleroal menos dos de e 1 , e 2 y e 3 deben compartir uno de esos puntos finales entre sí. Los gráficos lineales pueden caracterizarse en términos de nueve subgrafos prohibidos; [2] la garra es el más simple de estos nueve gráficos. Esta caracterización proporcionó la motivación inicial para estudiar gráficos sin garras. [1]
- Los gráficos de Bruijn (gráficos cuyos vértices representan cadenas binarias de n bits para algunos n , y cuyos bordes representan superposiciones de ( n - 1) bits entre dos cadenas) no tienen garras. Una forma de mostrar esto es a través de la construcción del gráfico de Bruijn para cadenas de n bits como el gráfico lineal del gráfico de Bruijn para cadenas ( n - 1) de bits.
- El complemento de cualquier gráfico sin triángulo no tiene garras. [3] Estos gráficos incluyen como caso especial cualquier gráfico completo .
- Los gráficos de intervalos adecuados , los gráficos de intervalos formados como gráficos de intersección de familias de intervalos en los que ningún intervalo contiene otro intervalo, no tienen garras, porque cuatro intervalos de intersección adecuados no pueden cruzarse en el patrón de una garra. [3] Lo mismo es cierto más generalmente para los gráficos de arco circular adecuados . [4]
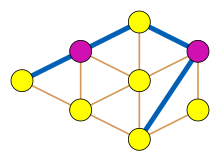
- El huso Moser , un gráfico de siete vértices utilizado para proporcionar un límite inferior para el número cromático del plano , no tiene garras.
- Las gráficas de varios poliedros y politopos están libres de garras, incluyendo la gráfica del tetraedro y más generalmente de cualquier símplex (una gráfica completa), la gráfica del octaedro y más generalmente de cualquier politopo cruzado ( isomorfo al gráfico de cóctel formado mediante la eliminación de una correspondencia perfecta de un gráfico completo), la gráfica de la regular de icosaedro , [5] y la gráfica de la de las células 16 .
- El gráfico Schläfli , un gráfico fuertemente regular con 27 vértices, no tiene garras. [5]
Reconocimiento [ editar ]
Es sencillo verificar que un gráfico dado con n vértices ym aristas esté libre de garras en el tiempo O ( n 4 ), probando cada 4 tuplas de vértices para determinar si inducen una garra. [6] Con más eficiencia y mayor complicación, uno puede probar si un gráfico no tiene garras al verificar, para cada vértice del gráfico, que el gráfico del complemento de sus vecinos no contenga un triángulo. Un gráfico contiene un triángulo si y solo si el cubo de su matriz de adyacencia contiene un elemento diagonal distinto de cero, por lo que puede encontrar un triángulo en el mismo límite de tiempo asintótico que n × n la multiplicación de matrices . [7] Por lo tanto, utilizando el algoritmo Coppersmith – Winograd , el tiempo total para este algoritmo de reconocimiento sin garras sería O ( n 3.376 ).
Kloks, Kratsch y Müller (2000) observan que en cualquier gráfico sin garras, cada vértice tiene como máximo 2 √ m vecinos; de lo contrario, según el teorema de Turán, los vecinos del vértice no tendrían suficientes bordes restantes para formar el complemento de un gráfico sin triángulo. Esta observación permite que la verificación de cada vecindario en el algoritmo basado en la multiplicación de matriz rápida descrito anteriormente se realice en el mismo límite de tiempo asintótico que la multiplicación de matriz de 2 √ m × 2 √ m , o más rápido para vértices con grados aún más bajos. El peor de los casos para este algoritmo ocurre cuando los vértices de Ω ( √ m ) tienen Ω ( √ m) vecinos cada uno, y los vértices restantes tienen pocos vecinos, por lo que su tiempo total es O ( m 3.376 / 2 ) = O ( m 1.688 ).
Enumeración [ editar ]
Debido a que los gráficos sin garras incluyen complementos de gráficos sin triángulos, el número de gráficos sin garras en n vértices crece al menos tan rápido como el número de gráficos sin triángulos, exponencialmente en el cuadrado de n . Los números de gráficos conectados sin garras en n nodos, para n = 1, 2, ... son
Si se permite desconectar los gráficos, el número de gráficos es aún mayor: son
Una técnica de Palmer, Read y Robinson (2002) permite que el número de gráficos cúbicos sin garras se cuente de manera muy eficiente, inusualmente para problemas de enumeración de gráficos .
Emparejamientos [ editar ]
Sumner (1974) e, independientemente, Las Vergnas (1975) demostraron que cada gráfico conectado sin garras con un número par de vértices tiene una coincidencia perfecta . [8] Es decir, existe un conjunto de aristas en el gráfico de modo que cada vértice es un punto final de exactamente una de las aristas coincidentes. El caso especial de este resultado para gráficos lineales implica que, en cualquier gráfico con un número par de aristas, uno puede dividir las aristas en trazados de longitud dos. Se pueden usar emparejamientos perfectos para proporcionar otra caracterización de los gráficos sin garras: son exactamente los gráficos en los que cada subgráfico inducido conectado de orden par tiene un emparejamiento perfecto. [8]
La prueba de Sumner muestra, más fuertemente, que en cualquier gráfico conectado sin garras uno puede encontrar un par de vértices adyacentes cuya eliminación deja conectado el gráfico restante. Para mostrar esto, Sumner encuentra un par de vértices u y v que están lo más separados posible en el gráfico, y elige w para ser un vecino de v que esté lo más lejos posible de u ; Como muestra, ni v ni w pueden encontrarse en la ruta más corta desde cualquier otro nodo hacia usted , por lo que la eliminación de v y wdeja el gráfico restante conectado. La eliminación repetida de pares de vértices coincidentes de esta manera forma una coincidencia perfecta en el gráfico sin garras dado.
La misma idea de prueba es más general si u es cualquier vértice, v es cualquier vértice que está muy lejos de ti , y w es cualquier vecino de v que está muy lejos de ti . Además, la eliminación de v y w del gráfico no cambia ninguna de las otras distancias desde u . Por lo tanto, el proceso de formar un emparejamiento mediante la búsqueda y eliminación de pares vw que están lo más lejos posible de usted puede llevarse a cabo mediante un solo recorrido de postorder de un primer árbol de búsqueda del gráfico, enraizado en u, en tiempo lineal. Chrobak, Naor y Novick (1989) proporcionan un algoritmo alternativo de tiempo lineal basado en la búsqueda de profundidad primero , así como algoritmos paralelos eficientes para el mismo problema.
Faudree, Flandrin y Ryjáček (1997) enumeran varios resultados relacionados, incluyendo los siguientes: ( r - 1) K 1 conectado , los gráficos libres de r de orden par tienen coincidencias perfectas para cualquier r ≥ 2; los gráficos sin garras de orden impar con un vértice de un grado como máximo se pueden dividir en un ciclo impar y una coincidencia; para cualquier k que sea como máximo la mitad del grado mínimo de un gráfico sin garras en el que k o el número de vértices es par, el gráfico tiene un factor k ; y, si es un gráfico libre de la garra es de (2 k + 1) comunicado con los, entonces cualquier k -Edge coincidente se puede extender a una correspondencia perfecta.
Conjuntos independientes [ editar ]
Un conjunto independiente en un gráfico lineal corresponde a una coincidencia en su gráfico subyacente, un conjunto de aristas de las cuales no hay dos que comparten un punto final. El algoritmo de flor de Edmonds (1965) encuentra una coincidencia máxima en cualquier gráfico en tiempo polinómico, lo que equivale a calcular un conjunto independiente máximo en gráficos lineales. Sbihi (1980) y Minty (1980) han ampliado esto independientemente a un algoritmo para todos los gráficos sin garras . [9]
Ambos enfoques utilizan la observación de que en los gráficos sin garras, ningún vértice puede tener más de dos vecinos en un conjunto independiente, por lo que la diferencia simétrica de dos conjuntos independientes debe inducir una subgrafía de grado como máximo en dos; es decir, es una unión de caminos y ciclos. En particular, si I es un conjunto independiente no máximo, difiere de cualquier conjunto independiente máximo por ciclos pares y los llamados caminos de aumento : caminos inducidos que alternan entre vértices que no están en I y vértices en I , y para los cuales ambos puntos finales solo tienen un vecino en I . Como la diferencia simétrica de Icon cualquier ruta de aumento que da un conjunto independiente más grande, la tarea se reduce a la búsqueda de rutas de aumento hasta que no se pueda encontrar más, de forma análoga a los algoritmos para encontrar coincidencias máximas.
El algoritmo de Sbihi recrea el paso de contracción en flor del algoritmo de Edmonds y agrega un paso de contracción de camarilla similar, pero más complicado . El enfoque de Minty es transformar la instancia del problema en un gráfico de línea auxiliar y usar el algoritmo de Edmonds directamente para encontrar las rutas de aumento. Después de una corrección por Nakamura y Tamura 2001 , el resultado de Minty también puede usarse para resolver en tiempo polinómico el problema más general de encontrar en gráficos sin garras un conjunto independiente de peso máximo. También se conocen generalizaciones de estos resultados a clases más amplias de gráficos. [9] Al mostrar un nuevo teorema de estructura , Faenza, Oriolo y Stauffer (2011) dio un algoritmo de tiempo cúbico, que también funciona en la configuración ponderada.
Colorear, camarillas y dominación [ editar ]
Un gráfico perfecto es un gráfico en el que el número cromático y el tamaño de la camarilla máxima son iguales, y en el que esta igualdad persiste en cada subgrafo inducido. Ahora se sabe (el fuerte teorema de la gráfica perfecta ) que las gráficas perfectas pueden caracterizarse como las gráficas que no tienen como subgrafos inducidos un ciclo impar o el complemento de un ciclo impar (un llamado agujero impar ). [10]Sin embargo, durante muchos años esto siguió siendo una conjetura no resuelta, solo probada para subclases especiales de gráficos. Una de estas subclases era la familia de gráficos sin garras: varios autores descubrieron que los gráficos sin garras sin ciclos impares y agujeros impares son perfectos. Los gráficos perfectos sin garras pueden reconocerse en el tiempo polinómico. En un gráfico perfecto sin garras, la vecindad de cualquier vértice forma el complemento de un gráfico bipartito . Es posible colorear gráficas perfectas sin garras, o encontrar camarillas máximas en ellas, en tiempo polinómico. [11]
| Problema no resuelto en matemáticas :
¿Los gráficos sin garras siempre tienen un número cromático de lista igual a su número cromático?
(Más problemas no resueltos en matemáticas) |
En general, es NP-difícil encontrar la camarilla más grande en un gráfico sin garras. [6] También es NP-difícil encontrar una coloración óptima del gráfico, porque (a través de gráficos de líneas) este problema generaliza el problema NP-difícil de calcular el índice cromático de un gráfico. [6] Por la misma razón, es NP-difícil encontrar un color que logre una relación de aproximación mejor que 4/3. Sin embargo, un algoritmo de coloración codicioso puede lograr una relación de aproximación de dos , porque el número cromático de un gráfico sin garras es mayor que la mitad de su grado máximo. Una generalización de la conjetura del color de la lista de bordes indica que, para gráficos sin garras, el número cromático de la listaes igual al número cromático; Estos dos números pueden estar muy separados en otros tipos de gráficos. [12]
Los gráficos sin garras tienen límites χ , lo que significa que cada gráfico sin garras de gran número cromático contiene una gran camarilla. Más fuertemente, del teorema de Ramsey se deduce que cada gráfica sin garras de gran grado máximo contiene una camarilla grande, de tamaño aproximadamente proporcional a la raíz cuadrada del grado. Para los gráficos conectados sin garras que incluyen al menos un conjunto independiente de tres vértices, es posible una relación más fuerte entre el número cromático y el tamaño de la camarilla: en estos gráficos, existe una camarilla de tamaño de al menos la mitad del número cromático. [13]
Aunque no todos los gráficos sin garras son perfectos, los gráficos sin garras satisfacen otra propiedad, relacionada con la perfección. Un gráfico se llama dominación perfecta si tiene un conjunto dominante mínimo que es independiente, y si la misma propiedad se mantiene en todas sus subgrafías inducidas. Los gráficos sin garras tienen esta propiedad. Para ver esto, deje que D sea un conjunto dominante en un gráfico sin garras, y suponga que v y w son dos vértices adyacentes en D ; entonces el conjunto de vértices dominado por v pero no por w debe ser una camarilla (de lo contrario vsería el centro de una garra). Si cada vértice en esta camarilla ya está dominado por al menos otro miembro de D , entonces v puede eliminarse produciendo un conjunto dominante independiente más pequeño, y de lo contrario v puede reemplazarse por uno de los vértices no dominados en su camarilla produciendo un conjunto dominante con Menos adyacencias. Al repetir este proceso de reemplazo, uno finalmente alcanza un conjunto dominante no mayor que D , por lo que, en particular, cuando el conjunto inicial D es un conjunto dominante mínimo, este proceso forma un conjunto dominante independiente igualmente pequeño. [14]
A pesar de esta propiedad de perfección de dominación, es NP-difícil determinar el tamaño del conjunto dominante mínimo en un gráfico sin garras. [6] Sin embargo, en contraste con la situación de las clases de gráficos más generales, encontrar el conjunto dominante mínimo o el conjunto dominante mínimo conectado en un gráfico sin garras es manejable con parámetros fijos : se puede resolver en el tiempo limitado por un polinomio en el tamaño del gráfico multiplicado por una función exponencial del tamaño del conjunto dominante. [15]
Estructura [ editar ]
Chudnovsky y Seymour (2005) resumen una serie de documentos en los que prueban una teoría de estructura para gráficos sin garras, análoga al teorema de estructura de gráfico para familias de gráficos cerrados menores probados por Robertson y Seymour, y a la teoría de estructura para gráficos perfectos que Chudnovsky, Seymour y sus coautores utilizaron para demostrar el teorema del gráfico perfecto fuerte. [10] La teoría es demasiado compleja para describirla en detalle aquí, pero para dar una idea de ello, es suficiente esbozar dos de sus resultados. Primero, para una subclase especial de gráficos sin garras que llaman gráficos de cuasi-línea (equivalentes, gráficos co-bipartitos locales), afirman que cada gráfico tiene una de dos formas:
- Un gráfico de intervalo circular difuso , una clase de gráficos representados geométricamente por puntos y arcos en un círculo, generalizando gráficos de arco circular adecuados.
- Un gráfico construido a partir de un multigrafo reemplazando cada borde por un gráfico de intervalo lineal difuso . Esto generaliza la construcción de un gráfico lineal, en el que cada borde del multigrafo se reemplaza por un vértice. Los gráficos de intervalos lineales difusos se construyen de la misma manera que los gráficos de intervalos circulares difusos, pero en una línea en lugar de en un círculo.
Chudnovsky y Seymour clasifican gráficos libres de garras conectados arbitrariamente en uno de los siguientes:
- Seis subclases específicas de gráficos sin garras. Tres de estos son gráficos de líneas, gráficos de arco circular apropiados y las subgrafías inducidas de un icosaedro; los otros tres implican definiciones adicionales.
- Gráficos formados en cuatro formas simples a partir de gráficos más pequeños sin garras.
- Gráficos antiprismáticos , una clase de gráficos densos definidos como los gráficos sin garras en los que cada cuatro vértices inducen una subgrafía con al menos dos aristas.
Gran parte del trabajo en su teoría de la estructura implica un análisis adicional de los gráficos antiprismáticos. El gráfico Schläfli , un gráfico fuertemente regular sin garras con parámetros srg (27,16,10,8), juega un papel importante en esta parte del análisis. Esta teoría de la estructura ha dado lugar a nuevos avances en combinatoria poliédrica y nuevos límites en el número cromático de gráficos sin garras, [5] [16] , así como a nuevos algoritmos manejables de parámetros fijos para conjuntos dominantes en gráficos sin garras.



No hay comentarios:
Publicar un comentario