En la teoría de grafos , un cactus (a veces llamado árbol de cactus ) es un gráfico conectado en el que dos ciclos simples tienen como máximo un vértice en común. De manera equivalente, es un gráfico conectado en el que cada borde pertenece a lo más a un ciclo simple, o (para cactus no trivial) en el que cada bloque (subgrafo máximo sin vértice cortado ) es un borde o un ciclo.
Propiedades [ editar ]
Los cactus son gráficas planas externas . Cada pseudotree es un cactus. Un gráfico no trivial es un cactus si y solo si cada bloque es un ciclo simple o un solo borde.
La familia de gráficos en la que cada componente es un cactus se cierra hacia abajo en operaciones menores de gráficos . Esta familia de gráficos puede caracterizarse por un solo menor prohibido , el gráfico de diamante de cuatro vértices formado al eliminar un borde del gráfico completo K 4 . [1]
Cactus triangular [ editar ]
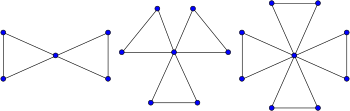
Un cactus triangular es un tipo especial de gráfico de cactus de modo que cada ciclo tiene una longitud de tres. Por ejemplo, los gráficos de amistad , gráficos formados a partir de una colección de triángulos unidos en un solo vértice compartido, son cactus triangulares. Además de ser gráficos de cactus, los cactus triangulares también son gráficos de bloques .
El cactus triangular más grande en cualquier gráfico se puede encontrar en tiempo polinómico usando un algoritmo para el problema de paridad matroide . Dado que los gráficos de cactus triangulares son gráficos planos , el cactus triangular más grande se puede usar como una aproximación al subgrafo plano más grande, un subproblema importante en la planarización . Como algoritmo de aproximación , este método tiene una relación de aproximación 4/9, la más conocida por el problema de subgrafía plana máxima. [2]
El algoritmo para encontrar el cactus triangular más grande está asociado con un teorema de Lovász y Plummer que caracteriza el número de triángulos en este cactus más grande. [3] Lovász y Plummer consideran pares de particiones de los vértices y bordes del gráfico dado en subconjuntos, con la propiedad de que cada triángulo del gráfico tiene dos vértices en una sola clase de la partición de vértices o los tres bordes en un solo clase de la partición de borde; llaman a un par de particiones con esta propiedad válida . Luego, el número de triángulos en el cactus triangular más grande es igual al máximo, sobre pares de particiones válidas y de
- ,
dónde es el número de vértices en el gráfico dado y es el número de clases de vértices que cumple la clase de borde .
Recientemente, se demostró un límite extremo apretado [4] que mostró que dado cualquier gráfico plano , siempre existe un subgrafo de cactus que contiene al menos fracción de las caras triangulares de . Este resultado implica un análisis directo del algoritmo de aproximación 4/9 para el problema del subgrafo plano máximo sin usar la fórmula min-max anterior.
La conjetura de Rosa [ editar ]
Una conjetura importante relacionada con el cactus triangular es la Conjetura de Rosa , llamada así por Alexander Rosa , que dice que todos los cactus triangulares son agraciados o casi agraciados. [5] Más precisamente
Todos los cactus triangulares con t ≡ 0, 1 mod 4 bloques son elegantes, y aquellos con t ≡ 2, 3 mod 4 son casi elegantes.
Algoritmos y aplicaciones [ editar ]
Algunos problemas de ubicación de instalaciones que son NP-hard para gráficos generales, así como algunos otros problemas de gráficos, pueden resolverse en tiempo polinómico para cactus. [6] [7]
Dado que los cactus son casos especiales de gráficas planas externas , se les puede resolver una serie de problemas de optimización combinatoria en gráficas en tiempo polinómico . [8]
Los cactus representan circuitos eléctricos que tienen propiedades útiles. Una aplicación temprana de cactus se asoció con la representación de amplificadores operacionales. [9] [10] [11]
Los cactus también se han utilizado recientemente en genómica comparativa como una forma de representar la relación entre diferentes genomas o partes de genomas. [12]
Si un cactus está conectado, y cada uno de sus vértices pertenece como máximo a dos bloques, entonces se llama cactus navideño . Cada gráfico poliédrico tiene una subgrafía de cactus navideño que incluye todos sus vértices, un hecho que juega un papel esencial en una prueba de Leighton & Moitra (2010) de que cada gráfico poliédrico tiene una incrustación codiciosa en el plano euclidiano , una asignación de coordenadas para los vértices para los cuales el reenvío codicioso logra enrutar mensajes entre todos los pares de vértices. [13]
En la teoría de grafos topológicos , los grafos cuyas incorporaciones celulares son todas planas son exactamente la subfamilia de los grafos de cactus con la propiedad adicional de que cada vértice pertenece como máximo a un ciclo. Estas gráficas tienen dos menores prohibidos, la gráfica de diamantes y la gráfica de amistad de cinco vértices . [14]
Historia [ editar ]
Los cactus fueron estudiados por primera vez bajo el nombre de árboles Husimi , otorgados por Frank Harary y George Eugene Uhlenbeck en honor al trabajo previo sobre estos gráficos por Kôdi Husimi . [15] [16] El mismo papel Harary – Uhlenbeck reserva el nombre de "cactus" para gráficos de este tipo en los que cada ciclo es un triángulo, pero ahora es estándar permitir ciclos de todas las longitudes.
Mientras tanto, el nombre árbol de Husimi comúnmente se refería a gráficos en los que cada bloque es un gráfico completo (de manera equivalente, los gráficos de intersección de los bloques en algún otro gráfico). Este uso tuvo poco que ver con el trabajo de Husimi, y el término gráfico de bloque más pertinente ahora se usa para esta familia; Sin embargo, debido a esta ambigüedad, esta frase se ha utilizado con menos frecuencia para referirse a los gráficos de cactus.
En el área matemática de la teoría de grafos , una jaula es un gráfico regular que tiene la menor cantidad de vértices posible para su circunferencia .
Formalmente, un gráfico ( r , g ) se define como un gráfico en el que cada vértice tiene exactamente r vecinos, y en el que el ciclo más corto tiene una longitud exactamente g . Se sabe que existe un gráfico ( r , g ) para cualquier combinación de r ≥ 2 yg ≥ 3. Una jaula ( r , g ) es un gráfico ( r , g ) con el menor número posible de vértices, entre todos los gráficos ( r , g ).
Si existe un gráfico de Moore con grado r y circunferencia g , debe ser una jaula. Además, los límites en los tamaños de los gráficos de Moore se generalizan en jaulas: cualquier jaula con circunferencia impar g debe tener al menos
vértices, y cualquier jaula con circunferencia uniforme g debe tener al menos
vértices Cualquier gráfico ( r , g ) con exactamente esta cantidad de vértices es, por definición, un gráfico de Moore y, por lo tanto, automáticamente una jaula.
Pueden existir múltiples jaulas para una combinación dada de r y g . Por ejemplo, hay tres jaulas no isomórficas (3,10), cada una con 70 vértices: la jaula Balaban 10 , la gráfica de Harries y la gráfica de Harries-Wong . Pero solo hay una (3,11) jaula: la balaban de 11 jaulas (con 112 vértices).
Jaulas conocidas [ editar ]
Un gráfico de grado uno no tiene ciclo, y un gráfico de grado dos conectado tiene una circunferencia igual a su número de vértices, por lo que las jaulas solo son de interés para r ≥ 3. La jaula ( r , 3) es un gráfico completo K r +1 en r +1 vértices, y la ( r , 4) -jaula es un gráfico bipartito completo K r , r en vértices 2 r .
Otras jaulas notables incluyen los gráficos de Moore:
- (3,5) -jaula: el gráfico de Petersen , 10 vértices
- (3,6) -jaula: el gráfico de Heawood , 14 vértices
- (3,8) -jaula: el gráfico Tutte-Coxeter , 30 vértices
- (3,10) -jaula: Balaban 10-jaula , 70 vértices
- (3,11) -jaula: Balaban 11-jaula , 112 vértices
- (4,5) -jaula: el gráfico de Robertson , 19 vértices
- (7,5) -jaula: El gráfico Hoffman – Singleton , 50 vértices.
- Cuando r - 1 es una potencia principal, las jaulas ( r , 6) son los gráficos de incidencia de planos proyectivos .
- Cuando r - 1 es una potencia principal, las jaulas ( r , 8) y ( r , 12) son polígonos generalizados .
Los números de vértices en las jaulas conocidas ( r , g ), para valores de r > 2 yg > 2, que no sean planos proyectivos y polígonos generalizados, son:
sol
r
| 3 | 4 4 | 5 5 | 6 6 | 7 7 | 8 | 9 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 4 4 | 6 6 | 10 | 14 | 24 | 30 | 58 | 70 | 112 | 126 |
| 4 4 | 5 5 | 8 | 19 | 26 | 67 | 80 | 728 | |||
| 5 5 | 6 6 | 10 | 30 | 42 | 170 | 2730 | ||||
| 6 6 | 7 7 | 12 | 40 | 62 | 312 | 7812 | ||||
| 7 7 | 8 | 14 | 50 | 90 |
Asintóticas [ editar ]
Para valores grandes de g , el límite de Moore implica que el número n de vértices debe crecer al menos exponencialmente en función de g . De manera equivalente, g puede ser como máximo proporcional al logaritmo de n . Más precisamente,
Se cree que este límite es estrecho o cercano ( Bollobás & Szemerédi 2002 ). Los límites inferiores más conocidos en g también son logarítmicos, pero con un factor constante más pequeño (lo que implica que n crece individualmente exponencialmente pero a una tasa mayor que el límite de Moore). Específicamente, los gráficos de Ramanujan ( Lubotzky, Phillips y Sarnak 1988 ) satisfacen el límite
Es poco probable que estos gráficos sean jaulas, pero su existencia da un límite superior al número de vértices necesarios en una jaula.
En las matemáticas y la informática , una canónica , lo normal o estándar de la forma de un objeto matemático es una manera estándar de presentar ese objeto como una expresión matemática . A menudo, es uno que proporciona la representación más simple de un objeto y que permite identificarlo de una manera única. [1] La distinción entre formas "canónicas" y "normales" varía de subcampo a subcampo. En la mayoría de los campos, una forma canónica especifica una representación única para cada objeto, mientras que una forma normal simplemente especifica su forma, sin el requisito de unicidad. [2]
La forma canónica de un entero positivo en representación decimal es una secuencia finita de dígitos que no comienza con cero. Más generalmente, para una clase de objetos en los que se define una relación de equivalencia , una forma canónica consiste en la elección de un objeto específico en cada clase. Por ejemplo:
- La forma normal de Jordan es una forma canónica para la similitud de la matriz .
- La forma escalonada de fila es una forma canónica, cuando uno considera como equivalente una matriz y su producto izquierdo por una matriz invertible .
En informática, y más específicamente en álgebra computacional , cuando se representan objetos matemáticos en una computadora, generalmente hay muchas formas diferentes de representar el mismo objeto. En este contexto, una forma canónica es una representación tal que cada objeto tiene una representación única ( siendo la canonicalización el proceso mediante el cual una representación se pone en su forma canónica). [3] Por lo tanto, la igualdad de dos objetos se puede probar fácilmente probando la igualdad de sus formas canónicas.
A pesar de esta ventaja, las formas canónicas con frecuencia dependen de elecciones arbitrarias (como ordenar las variables), que presentan dificultades para probar la igualdad de dos objetos que resultan en cálculos independientes. Por lo tanto, en álgebra computacional, la forma normal es una noción más débil: una forma normal es una representación tal que el cero se representa de manera única. Esto permite probar la igualdad al poner la diferencia de dos objetos en forma normal.
La forma canónica también puede significar una forma diferencial que se define de forma natural (canónica).
Definición [ editar ]
Dado un conjunto S de objetos con una relación de equivalencia R en S , se da una forma canónica al designar algunos objetos de S para que estén "en forma canónica", de modo que cada objeto considerado sea equivalente a exactamente un objeto en forma canónica. En otras palabras, las formas canónicas en S representan las clases de equivalencia, una vez y solo una vez. Para probar si dos objetos son equivalentes, es suficiente probar la igualdad en sus formas canónicas. Por lo tanto, una forma canónica proporciona un teorema de clasificación y más, ya que no solo clasifica cada clase, sino que también brinda un representante distinguido (canónico) para cada objeto de la clase.
Formalmente, una canonicalización con respecto a una relación de equivalencia R en un conjunto S es un mapeo c : S → S tal que para todos s , s 1 , s 2 ∈ S :
- c ( s ) = c ( c ( s )) ( idempotencia ),
- s 1 R s 2 si y solo si c ( s 1 ) = c ( s 2 ) (decisión), y
- s R c ( s ) (representatividad).
La propiedad 3 es redundante; se sigue aplicando 2 a 1.
En términos prácticos, a menudo es ventajoso poder reconocer las formas canónicas. También hay una pregunta práctica y algorítmica a considerar: ¿cómo pasar de un objeto dado s en S a su forma canónica s *? Las formas canónicas generalmente se usan para hacer que la operación con clases de equivalencia sea más efectiva. Por ejemplo, en aritmética modular., la forma canónica para una clase de residuo generalmente se toma como el número entero menos negativo en ella. Las operaciones en las clases se llevan a cabo combinando estos representantes y luego reduciendo el resultado a su menor residuo no negativo. El requisito de unicidad a veces se relaja, lo que permite que las formas sean únicas hasta una relación de equivalencia más fina, como permitir la reordenación de los términos (si no hay un orden natural en los términos).
Una forma canónica puede ser simplemente una convención o un teorema profundo. Por ejemplo, los polinomios se escriben convencionalmente con los términos en potencias descendentes: es más habitual escribir x 2 + x + 30 que x + 30 + x 2 , aunque las dos formas definen el mismo polinomio. Por el contrario, la existencia de la forma canónica de Jordan para una matriz es un teorema profundo.
Ejemplos [ editar ]
Nota: en esta sección, " hasta " alguna relación de equivalencia E significa que la forma canónica no es única en general, pero que si un objeto tiene dos formas canónicas diferentes, son E-equivalentes.
Notación de números grandes [ editar ]
Muchos matemáticos y científicos utilizan la forma estándar para escribir números extremadamente grandes de una manera más concisa y comprensible, siendo la más importante la notación científica . [4]
Teoría de números [ editar ]
- Representación canónica de un entero positivo.
- Forma canónica de una fracción continua
Álgebra lineal [ editar ]
| Objetos | A es equivalente a B si: | Forma normal | Notas |
|---|---|---|---|
| Matrices normales sobre los números complejos. | para alguna matriz unitaria U | Matrices diagonales (hasta reordenamiento) | Este es el teorema espectral |
| Matrices sobre los números complejos | para algunas matrices unitarias U y V | Matrices diagonales con entradas positivas reales (en orden descendente) | Valor singular de descomposición |
| Matrices sobre un campo algebraicamente cerrado | para alguna matriz invertible P | Forma normal de Jordan (hasta reordenamiento de bloques) | |
| Matrices sobre un campo algebraicamente cerrado | para alguna matriz invertible P | Forma canónica de Weyr (hasta reordenamiento de bloques) | |
| Matrices sobre un campo | para alguna matriz invertible P | Frobenius forma normal | |
| Matrices sobre un dominio ideal principal | para algunas matrices invertibles P y Q | Smith forma normal | La equivalencia es la misma que permite transformaciones elementales de fila y columna invertibles. |
| Matrices sobre los enteros | para alguna matriz unimodular U | Forma normal de Hermite | |
| Espacios vectoriales de dimensiones finitas sobre un campo K | A y B son isomorfos como espacios vectoriales | , n un entero no negativo |
Álgebra [ editar ]
| Objetos | A es equivalente a B si: | Forma normal |
|---|---|---|
| Módulos R generados finitamente con R un dominio ideal principal | A y B son isomorfos como módulos R | Descomposición primaria (hasta reordenamiento) o descomposición de factor invariante |
Geometría [ editar ]
- La ecuación de una línea: Ax + By = C , con A 2 + B 2 = 1 y C ≥ 0
- La ecuación de un círculo:
Por el contrario, hay formas alternativas para escribir ecuaciones. Por ejemplo, la ecuación de una línea puede escribirse como una ecuación lineal en forma punto-pendiente y pendiente-intersección .
- Todas las caras son planas
- Todos los bordes son tangentes a la esfera de la unidad, y
- El centroide del poliedro está en el origen. [5]
Sistemas integrables [ editar ]
Cada múltiple diferenciable tiene un paquete cotangente . Ese paquete siempre puede estar dotado de una cierta forma diferencial , llamada forma canónica única . Esta forma le da al paquete cotangente la estructura de una variedad simpléctica , y permite que los campos vectoriales en la variedad se integren por medio de las ecuaciones de Euler-Lagrange , o por medio de la mecánica hamiltoniana . Dichos sistemas de ecuaciones diferenciales integrables se denominan sistemas integrables .
Sistemas dinámicos [ editar ]
El estudio de los sistemas dinámicos se superpone con el de los sistemas integrables ; allí se tiene la idea de una forma normal (sistemas dinámicos) .
Geometría tridimensional [ editar ]
En el estudio de múltiples en tres dimensiones, uno tiene la primera forma fundamental , la segunda forma fundamental y la tercera forma fundamental .
Análisis funcional [ editar ]
| Objetos | A es equivalente a B si: | Forma normal |
|---|---|---|
| Espacios de Hilbert | Si A y B son espacios separables de Hilbert de dimensión infinita, entonces A y B son isométricamente isomorfos. | espacios de secuencia (hasta intercambiar el conjunto de índices I con otro conjunto de índices de la misma cardinalidad ) |
| Conmutativo -algebras con unidad | A y B son isomorfos como-algebras | El álgebra de funciones continuas en un espacio compacto de Hausdorff , hasta el homeomorfismo del espacio base. |
Lógica clásica [ editar ]
- Negación forma normal
- Forma normal conjuntiva
- Forma normal disyuntiva
- Forma normal algebraica
- Forma normal previa
- Skolem forma normal
- Forma canónica de Blake , también conocida como la suma completa de los principales implicantes, la suma completa o la forma primitiva disyuntiva
Teoría de conjuntos [ editar ]
Teoría de juegos [ editar ]
Teoría de la prueba [ editar ]
Sistemas de reescritura [ editar ]
La manipulación simbólica de una fórmula de una forma a otra se llama "reescritura" de esa fórmula. Uno puede estudiar las propiedades abstractas de reescribir fórmulas genéricas, estudiando la colección de reglas por las cuales las fórmulas pueden ser válidamente manipuladas. Estas son las "reglas de reescritura", una parte integral de un sistema de reescritura abstracta . Una pregunta común es si es posible traer alguna expresión genérica a una única forma común, la forma normal. Si diferentes secuencias de reescrituras todavía dan como resultado la misma forma, entonces esa forma puede denominarse una forma normal, y la reescritura se denomina confluente. No siempre es posible obtener una forma normal.
Cálculo Lambda [ editar ]
- Un término lambda está en forma beta normal si no es posible la reducción beta; El cálculo lambda es un caso particular de un sistema de reescritura abstracta. En el cálculo lambda sin tipo, por ejemplo, el términoNo tiene una forma normal. En el cálculo tipificado de lambda, cada término bien formado puede reescribirse en su forma normal.
Teoría de grafos [ editar ]
En la teoría de grafos , una rama de las matemáticas, canonización gráfico es el problema de encontrar una forma canónica de un gráfico dado G . Una forma canónica es un gráfico marcado Canon ( G ) que es isomorfo a G , de manera que cada gráfico que es isomorfo a G tiene la misma forma canónica como G . Por lo tanto, a partir de una solución al problema de canonización de grafos, también se podría resolver el problema del isomorfismo de grafos : para probar si dos grafos G y H son isomorfos, calcule sus formas canónicas Canon ( G ) y Canon ( H) y compruebe si estas dos formas canónicas son idénticas.
Computación [ editar ]
En informática , la reducción de datos a cualquier tipo de forma canónica se denomina comúnmente normalización de datos .
Por ejemplo, la normalización de la base de datos es el proceso de organizar los campos y las tablas de una base de datos relacional para minimizar la redundancia y la dependencia. [6]
En el campo de la seguridad del software , una vulnerabilidad común es la entrada maliciosa no verificada . La mitigación de este problema es la validación de entrada adecuada . Antes de que se pueda realizar la validación de entrada, la entrada debe normalizarse eliminando la codificación (por ejemplo, codificación HTML ) y reduciendo los datos de entrada a un único conjunto de caracteres común .
Se pueden normalizar otras formas de datos, típicamente asociadas con el procesamiento de señales (incluyendo audio e imágenes ) o aprendizaje automático , para proporcionar un rango limitado de valores.


























No hay comentarios:
Publicar un comentario