En la teoría de grafos , un gráfico conectado está conectado a k -edge si permanece conectado cada vez que se eliminan menos de k bordes.
El borde-conectividad de un gráfico es el más grande k para el que la gráfica es k conectado--Edge.
Conectividad Edge y la enumeración de k gráficas -Edge-conectada se estudió por Camille Jordan en 1869.
Definición formal [ editar ]
Dejar Ser un gráfico arbitrario. Si subgraph está conectado para todos dónde , entonces G está k -edge-conectado. La conectividad de borde dees el valor máximo k tal que G está k -edge-conectado. El conjunto más pequeño X cuya eliminación desconecta G es un corte mínimo en G .
La versión de conectividad de borde del teorema de Menger proporciona una caracterización alternativa y equivalente, en términos de caminos de disyunción de borde en el gráfico. Si y solo si cada dos vértices de G forman los puntos finales de k caminos, ninguno de los cuales comparte un borde entre sí, entonces G está k -edge-conectado. En una dirección esto es fácil: si existe un sistema de caminos como este, entonces cada conjunto X de menos de k bordes es disjunto de al menos uno de los caminos, y el par de vértices permanece conectado entre sí incluso después de Xesta borrado. En la otra dirección, la existencia de un sistema de caminos para cada par de vértices en un gráfico que no se puede desconectar mediante la eliminación de algunos bordes se puede probar utilizando el teorema de corte mínimo de flujo máximo de la teoría de flujos de red .
Conceptos relacionados [ editar ]
El grado mínimo de vértice proporciona un límite superior trivial en la conectividad de borde. Es decir, si un gráficose k conectado -Edge-entonces es necesario que k ≤ δ ( G ), donde δ ( G ) es el grado mínimo de cualquier vértice v ∈ V . Obviamente, eliminar todos los bordes incidentes en un vértice, v , desconectaría v del gráfico.
La conectividad de borde es el concepto dual de la circunferencia , la longitud del ciclo más corto en un gráfico, en el sentido de que la circunferencia de un gráfico plano es la conectividad de borde de su gráfico dual , y viceversa. Estos conceptos están unificados en la teoría de matroides por la circunferencia de un matroide , el tamaño del conjunto dependiente más pequeño en el matroide. Para un matroide gráfico , la circunferencia matroide es igual a la circunferencia del gráfico subyacente, mientras que para un matroide cográfico es igual a la conectividad de borde. [2]
Los gráficos conectados a 2 bordes también se pueden caracterizar por la ausencia de puentes , por la existencia de una descomposición del oído o por el teorema de Robbins según el cual estos son exactamente los gráficos que tienen una orientación fuerte . [3]
Aspectos computacionales [ editar ]
Hay un algoritmo de tiempo polinómico para determinar el mayor k para el cual un gráfico G es k conectado--Edge. Un algoritmo simple determinaría, para cada par (u, v) , el flujo máximo de u a v con la capacidad de todos los bordes en G establecida en 1 para ambas direcciones. Un gráfico es k conectado--Edge si y sólo si el flujo máximo de u a v es de al menos k para cualquier par (u, v) , por lo que k es el menos uv -flow entre todos (u, v) .
Si n es el número de vértices en el gráfico, este algoritmo simple funcionaría iteraciones del problema de flujo máximo, que se pueden resolver en hora. Por lo tanto, la complejidad del algoritmo simple descrito anteriormente es en total.
Un algoritmo mejorado resolverá el problema de flujo máximo para cada par (u, v) donde u se arregla arbitrariamente mientras v varía en todos los vértices. Esto reduce la complejidad ay es de sonido, ya que, si un corte de la capacidad de menos de k existe, que está obligado a separar u de otro vértice. Se puede mejorar aún más mediante un algoritmo de Gabow que se ejecuta en el peor de los casos.hora. [4]
La variante Karger-Stein del algoritmo de Karger proporciona un algoritmo aleatorio más rápido para determinar la conectividad, con tiempo de ejecución esperado. [5]
Un problema relacionado: la búsqueda del mínimo k subgrafo -Edge conectados abarca de G (que es: seleccionar el menor número posible aristas en G que su selección es k -Edge conectados) es NP-duro para.
| Gráfico de mariposa | |
|---|---|
 | |
| Vértices | 5 5 |
| Bordes | 6 6 |
| Radio | 1 |
| Diámetro | 2 |
| Circunferencia | 3 |
| Automorfismos | 8 ( D 4 ) |
| Número cromático | 3 |
| Índice cromático | 4 4 |
| Propiedades | Planar unidad de distancia euleriano No grácil |
| Tabla de gráficos y parámetros. | |
En el campo matemático de la teoría de grafos , el gráfico de mariposa (también llamado gráfico de corbatín y gráfico de reloj de arena ) es un gráfico plano no dirigido con 5 vértices y 6 aristas. [1] [2] Se puede construir uniendo 2 copias del gráfico de ciclo C 3 con un vértice común y, por lo tanto, es isomorfo al gráfico de amistad F 2 .
El gráfico de mariposa tiene diámetro 2 y circunferencia 3, radio 1, número cromático 3, índice cromático 4 y es a la vez Euleriano y un gráfico de centavo (esto implica que es una unidad de distancia y plana ). También es un gráfico conectado con 1 vértice y un gráfico conectado con 2 bordes .
Solo hay 3 gráficos simples no agraciados con cinco vértices. Uno de ellos es el gráfico de mariposa. Los otros dos son el gráfico de ciclo C 5 y el gráfico completo K 5 . [3]
Gráficos sin corbatines [ editar ]
Un gráfico no tiene pajarita si no tiene mariposa como subgrafo inducido . Los gráficos sin triángulo son gráficos sin corbatín, ya que cada mariposa contiene un triángulo.
En un gráfico conectado a k -vértice , se dice que un borde es k- contractible si la contracción del borde da como resultado un gráfico conectado a k . Ando, Kaneko, Kawarabayashi y Yoshimoto demostraron que cada gráfico sin corbata conectado por k -vértice tiene un borde k- contractible. [4]
Propiedades algebraicas [ editar ]
El grupo de automorfismo completo del gráfico de mariposa es un grupo de orden 8 isomorfo al grupo diédrico D 4 , el grupo de simetrías de un cuadrado , que incluye tanto rotaciones como reflexiones.
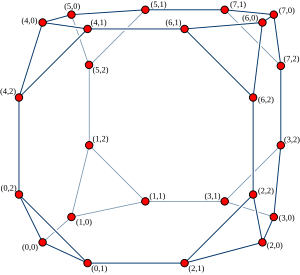
En la teoría de gráficos , los ciclos conectados al cubo es un gráfico cúbico no dirigido , formado al reemplazar cada vértice de un gráfico de hipercubo por un ciclo . Fue presentado por Preparata y Vuillemin (1981) para su uso como topología de red en computación paralela .
Definición [ editar ]
Los ciclos de orden n conectados al cubo (denotado CCC n ) se pueden definir como un gráfico formado a partir de un conjunto de n 2 n nodos, indexados por pares de números ( x , y ) donde 0 ≤ x <2 font="" nbsp="">n y 0 ≤ y < n . Cada uno de estos nodos está conectado a tres vecinos: ( x , ( y + 1) mod n ) , ( x , ( y - 1) mod n ) y ( x ⊕ 2 y , y ), donde "⊕" denota la exclusiva bit a bit u operación en números binarios.
Este gráfico también puede interpretarse como el resultado de reemplazar cada vértice de un gráfico hipercubo n- dimensional por un ciclo n- vértice. Los vértices del gráfico de hipercubos están indexados por los números x , y las posiciones dentro de cada ciclo por los números y .
Propiedades [ editar ]
Los ciclos de orden n conectados al cubo es el gráfico de Cayley de un grupo que actúa sobre palabras binarias de longitud n por rotación y volteo de bits de la palabra. [1] Los generadores utilizados para formar este gráfico de Cayley a partir del grupo son los elementos del grupo que actúan girando la palabra una posición hacia la izquierda, rotándola una posición hacia la derecha o volteando su primer bit. Debido a que es un gráfico de Cayley, es transitivo al vértice : hay una simetría del gráfico que asigna cualquier vértice a cualquier otro vértice.
El diámetro de los ciclos de orden n conectados al cubo es 2 n + ⌊n / 2⌋ - 2 para cualquier n ≥ 4; El punto más alejado de ( x , y ) es (2 n - x - 1, ( y + n / 2) mod n ). [2] Sýkora y Vrťo (1993) mostraron que el número de cruce de CCC n es ((1/20) + o (1)) 4 n .
Según la conjetura de Lovász , el gráfico del ciclo conectado al cubo siempre debe contener un ciclo hamiltoniano , y ahora se sabe que esto es cierto. En términos más generales, aunque estos gráficos no son pancíclicos , contienen ciclos de todos menos un número limitado de posibles longitudes pares, y cuando n es impar, también contienen muchas de las posibles longitudes impares de ciclos. [3]
Aplicación de procesamiento en paralelo [ editar ]
Los ciclos conectados a los cubos fueron investigados por Preparata y Vuillemin (1981) , quienes aplicaron estos gráficos como el patrón de interconexión de una red que conecta los procesadores en una computadora paralela . En esta aplicación, los ciclos conectados al cubo tienen las ventajas de conectividad de los hipercubos y solo requieren tres conexiones por procesador. Preparata y Vuillemin mostraron que un diseño plano basado en esta red tiene una complejidad óptima de área × tiempo 2 para muchas tareas de procesamiento en paralelo.
| Gráfico de ciclo | |
|---|---|

Un gráfico de ciclo de longitud 6
| |
| Vértices | norte |
| Bordes | norte |
| Circunferencia | norte |
| Automorfismos | 2 n ( D n ) |
| Número cromático | 3 si n es impar 2 de lo contrario |
| Índice cromático | 3 si n es impar 2 de lo contrario |
| Espectro | {2 cos (2 k π / n ); k = 1, ..., n } [1] |
| Propiedades | 2- vértice-transitivo regular Transitivo -borde Unidad distancia Hamiltoniana Euleriana |
| Notación | |
| Tabla de gráficos y parámetros. | |
En la teoría de grafos , un gráfico de ciclo o gráfico circular es un gráfico que consiste en un solo ciclo , o en otras palabras, cierto número de vértices (al menos 3) conectados en una cadena cerrada. El gráfico de ciclo con n vértices se llama C n . El número de vértices en C n es igual al número de aristas , y cada vértice tiene grado 2; es decir, cada vértice tiene exactamente dos bordes incidentes con él.
Terminología [ editar ]
Hay muchos sinónimos para "ciclo gráfico". Estos incluyen un gráfico de ciclo simple y un gráfico cíclico , aunque el último término se usa con menos frecuencia, porque también puede referirse a gráficos que simplemente no son acíclicos . Entre los teóricos de gráficos, también se usan a menudo ciclo , polígono o n -gon . El término n -cycle a veces se usa en otras configuraciones. [2] Un ciclo con un número par de vértices se llama ciclo par ; un ciclo con un número impar de vértices se llama ciclo impar .
Propiedades [ editar ]
Un gráfico de ciclo es:
- Coloreable de 2 bordes , si y solo si tiene un número par de vértices
- 2-regular
- 2 vértices coloreables , si y solo si tiene un número par de vértices. Más generalmente, un gráfico es bipartito si y solo si no tiene ciclos impares ( Kőnig , 1936).
- Conectado
- Eulerian
- Hamiltoniano
- Un gráfico de distancia unitaria
Adicionalmente:
- Como los gráficos de ciclo se pueden dibujar como polígonos regulares , las simetrías de un ciclo n son las mismas que las de un polígono regular con n lados, el grupo diédrico de orden 2 n . En particular, existen simetrías que llevan cualquier vértice a cualquier otro vértice, y cualquier borde a cualquier otro borde, por lo que el ciclo n es un gráfico simétrico .
De manera similar a los gráficos platónicos , los gráficos de ciclo forman los esqueletos de los dihedra . Sus duales son los gráficos dipolares , que forman los esqueletos de los hosohedra .
Gráfico de ciclo dirigido [ editar ]
Un gráfico de ciclo dirigido es una versión dirigida de un gráfico de ciclo, con todos los bordes orientados en la misma dirección.
En un gráfico dirigido , un conjunto de bordes que contiene al menos un borde (o arco ) de cada ciclo dirigido se denomina conjunto de arco de retroalimentación . Del mismo modo, un conjunto de vértices que contiene al menos un vértice de cada ciclo dirigido se denomina conjunto de vértices de retroalimentación .
Un gráfico de ciclo dirigido tiene un grado de entrada uniforme 1 y un grado de salida uniforme 1.
Los gráficos de ciclo dirigido son gráficos de Cayley para grupos cíclicos (véase, por ejemplo, Trevisan).















No hay comentarios:
Publicar un comentario