TEORÍA DE TÉRMINOS DE GRAFOS

En la teoría de grafos , un gráfico clique de un grafo no dirigido G es otro gráfico K ( G ) que representa la estructura de camarillas en G .

Los gráficos de camarilla se discutieron al menos en 1968 ^[1] y en 1971. se dio una caracterización de los gráficos de camarilla .

Definición formal [ editar ]

A clique de un gráfico G es un conjunto X de vértices de G con la propiedad de que cada par de vértices distintos en X son adyacentes en G . Una camarilla máxima de un gráfico G es una camarilla X de vértices de G , de modo que no haya una camarilla Y de vértices de G que contenga todo X y al menos otro vértice.

Dado un gráfico G , su gráfico de camarilla K ( G ) es un gráfico tal que

• cada vértice de K ( G ) representa una camarilla máxima de G ; y
• dos vértices de K ( G ) son adyacentes cuando las camarillas subyacentes en G comparten al menos un vértice en común.

El gráfico clique K ( G ) también se puede caracterizar como el gráfico de intersección de la máxima camarillas de G . ^[3]

Caracterización [ editar ]

Un gráfico H es el gráfico de camarilla K ( G ) de otro gráfico si y solo si existe una colección C de camarillas en H cuya unión cubre todos los bordes de H , de modo que C forme una familia Helly . Esto significa que, si S es un subconjunto de C con la propiedad de que cada dos miembros de S tienen una intersección no vacía, entonces S también debería tener una intersección no vacía. Sin embargo, las camarillas en C no necesariamente tienen que ser camarillas máximas. ^[2]

Cuando H  = K ( G ), se puede construir una familia C de este tipo en la que cada camarilla en C corresponde a un vértice v en G , y consiste en las camarillas en G que contienen v . Estas camarillas todos tienen v en su intersección, de modo que formen una camarilla en H . La familia C construida de esta manera tiene la propiedad Helly, porque cualquier subfamilia de C con intersecciones por pares no vacías debe corresponder a una camarilla en G, que se puede extender a una camarilla máxima que pertenece a la intersección de la subfamilia. ^[2]

A la inversa, cuando H tiene una familia Helly C de sus camarillas, que abarca todos los bordes de H , entonces es el gráfico clique K ( G ) para un gráfico G cuyos vértices son la unión de la desunión de los vértices de H y los elementos de C . Este gráfico G tiene un borde para cada par de camarillas en C con intersección no vacía, y para cada par de vértices de H y una camarilla en C que lo contiene. Sin embargo, no contiene ningún bordes de conexión pares de vértices en H . Las camarillas máximas en este gráficoG consisten cada uno en un vértice de H junto con todas las camarillas en C que lo contienen, y su gráfico de intersección es isomorfo a  H . ^[2]

Sin embargo, esta caracterización no conduce a algoritmos eficientes: el problema de reconocer si un gráfico dado es un gráfico de camarilla es NP-completo .

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Construcción de un gráfico hereditario de distancia de ancho de camarilla 3 mediante uniones disjuntas, reetiquetados y uniones de etiquetas. Las etiquetas de vértice se muestran como colores.

En teoría de grafos , el ancho de camarilla de un grafo $${\ displaystyle G}es un parámetro que describe la complejidad estructural de la gráfica; está estrechamente relacionado con el ancho del árbol , pero a diferencia del ancho del árbol, puede limitarse incluso para gráficos densos . Se define como el número mínimo de etiquetas necesarias para construir$${\ displaystyle G} mediante las siguientes 4 operaciones:

1. Creación de un nuevo vértice v con etiqueta i (anotado i (v) )
2. Unión disjunta de dos gráficos etiquetados G y H (denotado$${\ displaystyle G \ oplus H} )
3. Unirse por un borde cada vértice etiquetado como i a cada vértice etiquetado como j (denotado η (i, j) ), donde$${\ displaystyle i \ neq j}
4. Cambiar el nombre de la etiqueta i a la etiqueta j (denotado ρ ( i , j ))

Los gráficos de ancho de camarilla acotados incluyen los cogramas y los gráficos hereditarios de distancia . Aunque es NP-difícil calcular el ancho de la camarilla cuando no está acotado, y se desconoce si se puede calcular en tiempo polinómico cuando está acotado, se conocen algoritmos de aproximación eficientes para el ancho de la camarilla. Basado en estos algoritmos y en el teorema de Courcelle , muchos problemas de optimización de gráficos que son NP-hard para gráficos arbitrarios pueden resolverse o aproximarse rápidamente en los gráficos de ancho de camarilla acotado.

Las secuencias de construcción que subyacen al concepto de ancho de camarilla fueron formuladas por Courcelle , Engelfriet y Rozenberg en 1990 ^[1] y por Wanke (1994) . El nombre "ancho de camarilla" fue utilizado para un concepto diferente por Chlebíková (1992) . Para 1993, el término ya tenía su significado actual. 

Clases especiales de gráficos [ editar ]

Los cográficos son exactamente los gráficos con un ancho de camarilla como máximo 2. ^[3] Cada gráfico de distancia hereditaria tiene como máximo un ancho de camarilla 3. Sin embargo, el ancho de camarilla de los gráficos de intervalos unitarios no tiene límites (en función de su estructura de cuadrícula). ^[4] Del mismo modo, el ancho de camarilla de los gráficos de permutación bipartita no tiene límites (basado en una estructura de cuadrícula similar). ^[5] Basado en la caracterización de los cográficos como los gráficos sin subgrafo inducido isomorfo a un camino sin acordes con cuatro vértices, se ha clasificado el ancho de camarilla de muchas clases de gráficos definidos por subgrafos inducidos prohibidos. ^[6]

Otros gráficos con ancho de camarilla acotado incluyen las potencias de la hoja k para valores acotados de k ; Estas son las subgrafías inducidas de las hojas de un árbol T en la potencia del gráfico T ^k . Sin embargo, las potencias de las hojas con exponentes ilimitados no tienen un ancho de camarilla acotado. ^[7]

Límites [ editar ]

Courcelle y Olariu (2000) y Corneil y Rotics (2005) demostraron los siguientes límites en el ancho de la camarilla de ciertos gráficos:

• Si un gráfico tiene un ancho de camarilla como máximo k , entonces también lo tiene cada subgrafo inducido del gráfico. ^[8]
• El gráfico de complemento de un gráfico de ancho de camarilla k tiene un ancho de camarilla como máximo 2 k . ^[9]
• Los gráficos de ancho de árbol w tienen ancho de camarilla como máximo 3 · 2 ^{w - 1} . La dependencia exponencial en este límite es necesaria: existen gráficos cuyo ancho de camarilla es exponencialmente mayor que su ancho de árbol. ^[10] En la otra dirección, los gráficos de ancho de camarilla acotado pueden tener un ancho de árbol ilimitado; por ejemplo, los gráficos completos n -vertex tienen ancho de camarilla 2 pero ancho de árbol n -1 . Sin embargo, los gráficos de ancho de camarilla k que no tienen un gráfico bipartito completo K _t , t como subgrafo tienen un ancho de árbol como máximo 3 k ( t - 1) - 1 . Por lo tanto, para cada familia de gráficos dispersos , tener un ancho de árbol limitado es equivalente a tener un ancho de camarilla limitado. ^[11]
• Otro parámetro de gráfico, el ancho de rango , está limitado en ambas direcciones por el ancho de camarilla: ancho de rango ≤ ancho de camarilla ≤ 2 ancho de ^{rango + 1} . ^[12]

Además, si un gráfico G tiene un ancho de camarilla k , entonces la potencia del gráfico G ^c tiene un ancho de camarilla como máximo 2 kc ^k . ^[13] Aunque hay una brecha exponencial tanto en el límite para el ancho de la camarilla del ancho del árbol como en el límite para el ancho de la camarilla de las potencias del gráfico, estos límites no se componen entre sí: si un gráfico G tiene el ancho del árbol w , entonces G ^c tiene ancho de camarilla como máximo 2 ( c + 1) ^{w + 1} - 2 , solo exponencialmente individual en el ancho del árbol. ^[14]

Complejidad computacional [ editar ]

Problema no resuelto en matemáticas : ¿Se pueden reconocer las gráficas de ancho de camarilla acotada en tiempo polinómico? (Más problemas no resueltos en matemáticas)

Muchos problemas de optimización que son NP-hard para clases más generales de gráficos pueden resolverse eficientemente mediante programación dinámica en gráficos de ancho de camarilla acotado, cuando se conoce una secuencia de construcción para estos gráficos. ^[15] [16] En particular, cada propiedad de gráfico que se puede expresar en la lógica de segundo orden monádica de MSO ₁ (una forma de lógica que permite la cuantificación sobre conjuntos de vértices) tiene un algoritmo de tiempo lineal para gráficos de ancho de camarilla acotado, por una forma del teorema de Courcelle . ^[dieciséis]

También es posible encontrar coloraciones gráficas óptimas o ciclos hamiltonianos para gráficos de ancho de camarilla acotado en tiempo polinómico, cuando se conoce una secuencia de construcción, pero el exponente del polinomio aumenta con el ancho de camarilla, y la evidencia de la teoría de la complejidad computacional muestra que esta dependencia es probable que sea necesaria. ^[17] Las gráficas de ancho de camarilla acotada tienen un límite χ , lo que significa que su número cromático es como máximo una función del tamaño de su camarilla más grande. ^[18]

Los gráficos del ancho de camarilla tres se pueden reconocer, y se puede encontrar una secuencia de construcción para ellos, en tiempo polinómico, utilizando un algoritmo basado en la descomposición dividida . ^[19] Para gráficos de ancho de camarilla no acotado, es NP-difícil calcular el ancho de camarilla exactamente, y también NP-hard obtener una aproximación con un error aditivo sublineal. ^[20] Sin embargo, cuando el ancho de la camarilla está acotado, es posible obtener una secuencia de construcción de ancho acotado (exponencialmente mayor que el ancho real de la camarilla) en el tiempo polinómico. ^[21] Permanece abierto si el ancho exacto de la camarilla, o una aproximación más estricta, se puede calcular en un tiempo manejable de parámetros fijos, si puede calcularse en tiempo polinómico para cada límite fijo en el ancho de la camarilla, o incluso si las gráficas del ancho de camarilla cuatro pueden reconocerse en el tiempo polinómico. ^[20]

Relación con el ancho de árbol [ editar ]

La teoría de los gráficos de ancho de camarilla acotada se asemeja a la de los gráficos de ancho de árbol acotado , pero a diferencia del ancho de árbol, permite gráficos densos . Si una familia de gráficos tiene un ancho de camarilla delimitado, entonces tiene un ancho de árbol delimitado o cada gráfico bipartito completo es un subgrafo de un gráfico de la familia. ^{[11] El} ancho de árbol y el ancho de la camarilla también están conectados a través de la teoría de los gráficos lineales : una familia de gráficos tiene un ancho de árbol acotado si y solo si sus gráficos de línea tienen un ancho de camarilla acotado.

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

El gráfico de Turán T (13,4), un ejemplo de cografía

En la teoría de grafos , un cograph , o gráfico complementar reducible , o P ₄ gráfico exento , es un gráfico que puede ser generada a partir de la de un solo vértice gráfico K ₁ por complementación y unión de la desunión . Es decir, la familia de los cográficos es la clase de gráficos más pequeña que incluye K ₁ y está cerrada bajo complementación y unión disjunta.

Varios autores han descubierto coógrafos de forma independiente desde la década de 1970; Las primeras referencias incluyen a Jung (1978) , Lerchs (1971) , Seinsche (1974) y Sumner (1974) . También se les ha llamado gráficos D * , ^[1] gráficos hereditarios de Dacey (después del trabajo relacionado de James C. Dacey Jr. sobre redes ortomodulares ), ^[2] y gráficos de 2 paridades . ^[3] Tienen una descomposición estructural simple que involucra una unión disjunta y un gráfico complementariooperaciones que pueden representarse de manera concisa por un árbol etiquetado y usarse algorítmicamente para resolver eficientemente muchos problemas, como encontrar la camarilla máxima que es difícil en las clases de gráficos más generales.

Casos especiales de los cographs incluyen los gráficos completos , grafo bipartito completo , gráficos de racimo , y gráficos de umbral . Los cogramas son, a su vez, casos especiales de los gráficos de distancia hereditaria , gráficos de permutación , gráficos de comparabilidad y gráficos perfectos .

Definición [ editar ]

Construcción recursiva [ editar ]

Cualquier cograph puede construirse usando las siguientes reglas:

1. cualquier gráfico de vértice es un cograma;
2. Si $${\ displaystyle G}es un cograph, también lo es su gráfico complementario $${\ displaystyle {\ overline {G}}};
3. Si $${\ displaystyle G} y $${\ displaystyle H} son cografías, también lo es su unión disjunta $${\ displaystyle G \ cup H}.

Los cogramas pueden definirse como los gráficos que pueden construirse utilizando estas operaciones, comenzando por los gráficos de un solo vértice. ^[4] Alternativamente, en lugar de usar la operación de complemento, uno puede usar la operación de unión, que consiste en formar la unión disjunta$${\ displaystyle G \ cup H} y luego agregando un borde entre cada par de vértices de $${\ displaystyle G} y un vértice de $${\ displaystyle H}.

Otras caracterizaciones [ editar ]

Se pueden dar varias caracterizaciones alternativas de cografías. Entre ellos:

• Un cograph es un gráfico que no contiene la ruta P ₄ en 4 vértices (y, por lo tanto, de longitud 3) como un subgraph inducido . Es decir, un gráfico es un cograma si y solo si hay cuatro vértices$${\ displaystyle v_ {1}, v_ {2}, v_ {3}, v_ {4}}, Si $${\ displaystyle \ {v_ {1}, v_ {2} \}, \ {v_ {2}, v_ {3} \}} y $${\ displaystyle \ {v_ {3}, v_ {4} \}} son bordes de la gráfica, entonces al menos uno de $${\ displaystyle \ {v_ {1}, v_ {3} \}, \ {v_ {1}, v_ {4} \}} o $${\ displaystyle \ {v_ {2}, v_ {4} \}}También es una ventaja. ^[4]
• Una cografía es una gráfica cuyas subgrafías inducidas tienen la propiedad de que cualquier camarilla máxima se cruza con cualquier conjunto independiente máximo en un solo vértice.
• Un cograph es un gráfico en el que cada subgraph inducido no trivial tiene al menos dos vértices con los mismos vecindarios.
• Un cograph es un gráfico en el que cada subgraph inducido conectado tiene un complemento desconectado.
• Un cograph es un gráfico cuyos subgrafos inducidos conectados tienen un diámetro como máximo 2.
• Un cograph es un gráfico en el que cada componente conectado es un gráfico de distancia hereditaria con un diámetro máximo de 2.
• Un cograph es un gráfico con ancho de camarilla como máximo 2. ^[5]
• Un cograph es un gráfico de comparabilidad de un orden parcial paralelo en serie . ^[1]
• Un cograph es un gráfico de permutación de una permutación separable . ^[6]
• Un cograph es un gráfico cuyas terminaciones cordales mínimas son gráficos trivialmente perfectos . ^[7]
• Una cografía es una gráfica hereditariamente bien coloreada , una gráfica tal que cada coloración codiciosa de cada subgrafía inducida utiliza una cantidad óptima de colores. ^[8]
• Un gráfico es un cograma si y solo si cada orden de vértices del gráfico es un orden perfecto , ya que no tener P ₄ significa que no existirá ninguna obstrucción a un orden perfecto en ningún orden de vértices.

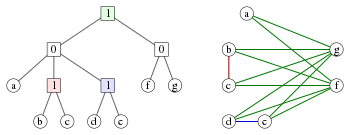
Cotrees [ editar ]

Un cotree y el cograph correspondiente. Cada borde ( u , v ) en el cograph tiene un color coincidente con el ancestro menos común de u y v en el árbol.

Una cotree es un árbol en el que los nodos internos están etiquetados con los números 0 y 1. Cada cotree T define un cograma G que tiene las hojas de T como vértices, y en el que el subárbol enraizado en cada nodo de T corresponde al subgrafo inducido en G definido por el conjunto de hojas que descienden de ese nodo:

• Un subárbol que consiste en un solo nodo de hoja corresponde a un subgráfico inducido con un solo vértice.
• Un subárbol enraizado en un nodo con la etiqueta 0 corresponde a la unión de los subgráficos definidos por los hijos de ese nodo.
• Un subárbol enraizado en un nodo etiquetado como 1 corresponde a la unión de los subgráficos definidos por los hijos de ese nodo; es decir, formamos la unión y agregamos un borde entre cada dos vértices correspondientes a las hojas en diferentes subárboles. Alternativamente, la unión de un conjunto de gráficos se puede ver como formada complementando cada gráfico, formando la unión de los complementos y luego complementando la unión resultante.

Una forma equivalente de describir el cograma formado a partir de una cotree es que dos vértices están conectados por un borde si y solo si el ancestro común más bajo de las hojas correspondientes está marcado por 1. Por el contrario, cada cograph puede representarse de esta manera por una cotree . Si requerimos que las etiquetas en cualquier ruta raíz-hoja de este árbol alternen entre 0 y 1, esta representación es única. ^[4]

Propiedades computacionales [ editar ]

Los cográficos pueden reconocerse en tiempo lineal y construirse una representación en árbol, utilizando descomposición modular , ^[9] refinamiento de partición , ^[10] LexBFS , ^[11] o descomposición dividida . ^[12] Una vez que se ha construido una representación cotree, muchos problemas gráficos familiares pueden resolverse mediante simples cálculos ascendentes en los cotrees.

Por ejemplo, para encontrar la camarilla máxima en una cografía, calcule en orden ascendente la camarilla máxima en cada subgrafía representada por un subárbol de la cotree. Para un nodo etiquetado como 0, la camarilla máxima es la máxima entre las camarillas calculadas para los hijos de ese nodo. Para un nodo etiquetado como 1, la camarilla máxima es la unión de las camarillas calculadas para los hijos de ese nodo y tiene un tamaño igual a la suma de los tamaños de las camarillas de los niños. Por lo tanto, al maximizar y sumar alternativamente los valores almacenados en cada nodo del árbol, podemos calcular el tamaño máximo de la camarilla, y al maximizar y tomar uniones alternativamente, podemos construir la camarilla máxima en sí. Cálculos de árbol ascendentes similares permiten el conjunto independiente máximo , número de coloración de vértices, cobertura máxima de la camarilla y Hamiltonicity (es decir, la existencia de un ciclo hamiltoniano ) que se calculará en tiempo lineal a partir de una representación de un cograma. ^[4] Debido a que los cográficos tienen un ancho de camarilla acotado, el teorema de Courcelle se puede usar para probar cualquier propiedad en la lógica de gráficos de segundo orden monádica (MSO ₁ ) en los coógrafos en tiempo lineal. ^[13]

El problema de probar si un gráfico dado está a k vértices de distancia y / o t bordes lejos de un cograma es manejable con parámetros fijos . ^[14] El decidir si un gráfico puede ser k -Edge-eliminado a una cograph puede ser resuelto de O ^* (2.415 ^k tiempo), ^[15] y k editado--Edge a un cograph en O ^* (4.612 ^k ). ^[16] Si se puede encontrar el subgrafo de cografía inducido más grande de un gráfico eliminando k vértices del gráfico, se puede encontrar en el tiempo O ^* (3.30 ^k ). ^[15]

Dos cografías son isomorfas si y solo si sus cotrees (en la forma canónica sin dos vértices adyacentes con la misma etiqueta) son isomorfas. Debido a esta equivalencia, se puede determinar en tiempo lineal si dos cografías son isomorfas, construyendo sus cotrees y aplicando una prueba de isomorfismo de tiempo lineal para árboles etiquetados. ^[4]

Si H es un subgrafo inducido de un cografo G , entonces H es en si mismo un cografo; El árbol para H puede formarse eliminando algunas de las hojas del árbol para G y luego suprimiendo los nodos que tienen un solo hijo. Del teorema del árbol de Kruskal se deduce que la relación de ser un subgrafo inducido es un cuasi ordenamiento en los coógrafos. ^[17] Por lo tanto, si una subfamilia de los cográficos (como los cogramas planos ) se cierra bajo operaciones de subgrafía inducidas, entonces tiene un número finito de subgrafías inducidas prohibidas. Computacionalmente, esto significa que la membresía de prueba en una subfamilia de este tipo se puede realizar en tiempo lineal, mediante el uso de un cálculo de abajo hacia arriba en la pantalla de un gráfico determinado para probar si contiene alguno de estos subgrafos prohibidos. Sin embargo, cuando los tamaños de dos cogramas son variables, probar si uno de ellos es un subgrafo inducido del otro es NP completo . ^[18]

Los cogramas juegan un papel clave en los algoritmos para reconocer las funciones de lectura única . ^[19]

Enumeración [ editar ]

El número de cografías conectadas con n vértices, para n = 1, 2, 3, ..., es:

1, 1, 2, 5, 12, 33, 90, 261, 766, 2312, 7068, 21965, 68954, ... (secuencia A000669 en el OEIS )

Para n > 1 hay el mismo número de cografías desconectadas, porque para cada cografía se conecta exactamente una de ellas o su gráfica complementaria .

Familias gráficas relacionadas [ editar ]

Subclases [ editar ]

Cada gráfico completo K _n es un cograma, con un árbol que consiste en un solo nodo y n hojas. Del mismo modo, cada gráfico bipartito completo K _a , b es un cograma. Su coárbol tiene sus raíces en una 1-nodo que tiene dos hijos 0-nodo, una con una hoja de niños y una con b niños de hojas. Un gráfico de Turán puede estar formado por la unión de una familia de conjuntos independientes de igual tamaño; por lo tanto, también es un cograph, con un árbol enraizado en un nodo 1 que tiene un nodo 0 secundario para cada conjunto independiente.

Cada gráfico de umbral también es un cograma. Se puede formar un gráfico de umbral agregando repetidamente un vértice, ya sea conectado a todos los vértices anteriores o a ninguno de ellos; cada una de estas operaciones es una de las operaciones de unión o unión disjuntas mediante las cuales se puede formar un árbol. ^[20]

Superclases [ editar ]

La caracterización de los cogramas por la propiedad de que cada camarilla y conjunto independiente máximo tienen una intersección no vacía es una versión más fuerte de la propiedad definitoria de gráficos muy perfectos , en la que cada subgrafo inducido contiene un conjunto independiente que intersecta a todas las camarillas máximas. En un gráfico, cada conjunto independiente máximo se cruza con todas las camarillas máximas. Por lo tanto, cada cografía es muy perfecta. ^[21]

El hecho de que los coógrafos sean libres de P ₄ implica que son perfectamente ordenables . De hecho, cada orden de vértices de un cograma es un orden perfecto, lo que implica que el hallazgo máximo de la camarilla y la coloración mínima se pueden encontrar en tiempo lineal con cualquier coloración codiciosa y sin la necesidad de una descomposición del árbol.

Cada cograph es un gráfico de distancia hereditaria , lo que significa que cada ruta inducida en un cograph es una ruta más corta . Los cogramas pueden caracterizarse entre los gráficos hereditarios de distancia como teniendo un diámetro dos en cada componente conectado. Cada cograph es también un gráfico de comparabilidad de un orden parcial paralelo en serie , obtenido al reemplazar las operaciones de unión y unión disjuntas por las cuales el cograph se construyó mediante operaciones de unión disjunta y suma ordinal en órdenes parciales. Debido a que los gráficos muy perfectos, los gráficos perfectamente ordenables, los gráficos de distancia hereditaria y los gráficos de comparabilidad son todos gráficos perfectos , los cogramas también son perfectos.