TEORÍA DE TÉRMINOS DE GRAFOS

En el campo matemático de la teoría de grafos , un automorfismo de un gráfico es una forma de simetría en la cual el gráfico se mapea sobre sí mismo mientras se preserva la conectividad borde-vértice.

Formalmente, un automorfismo de un gráfico G  = ( V , E ) es una permutación σ del conjunto de vértices V , de modo que el par de vértices ( u , v ) forman un borde si y solo si el par (σ ( u ), σ ( v )) también forman una arista. Es decir, es un isomorfismo gráfico de G a sí mismo. Los automorfismos pueden definirse de esta manera tanto para gráficos dirigidos como para gráficos no dirigidos . La composiciónde dos automorfismos es otro automorfismo, y el conjunto de automorfismos de un gráfico dado, bajo la operación de composición, forma un grupo , el grupo de automorfismo del gráfico. En la dirección opuesta, según el teorema de Frucht , todos los grupos pueden representarse como el grupo de automorfismo de un gráfico conectado, de hecho, de un gráfico cúbico . 

Complejidad computacional [ editar ]

Construir el grupo de automorfismo es al menos tan difícil (en términos de su complejidad computacional ) como resolver el problema del isomorfismo del gráfico , determinando si dos gráficos correspondientes corresponden vértice por vértice y borde por borde. Para, G y H son isomórficos si y solo si el gráfico desconectado formado por la unión disjunta de los gráficos G y H tiene un automorfismo que intercambia los dos componentes. ^[3] De hecho, solo contar los automorfismos es el tiempo polinomial equivalente al isomorfismo gráfico ^[4]

Este dibujo del gráfico de Petersen muestra un subgrupo de sus simetrías, isomorfo al grupo diédrico D ₅ , pero el gráfico tiene simetrías adicionales que no están presentes en el dibujo. Por ejemplo, dado que el gráfico es simétrico , todos los bordes son equivalentes.

El problema del automorfismo gráfico es el problema de probar si un gráfico tiene un automorfismo no trivial. Pertenece a la clase NP de complejidad computacional. Similar al problema del isomorfismo gráfico, se desconoce si tiene un algoritmo de tiempo polinomial o si es NP completo . ^[5] Existe un algoritmo de tiempo polinomial para resolver el problema del automorfismo de gráficos para gráficos en los que los grados de vértice están delimitados por una constante. ^[3] El problema del automorfismo del gráfico es polinomial en tiempo múltiple reducible al problema del isomorfismo del gráfico, pero se desconoce la reducción inversa. ^{[4] [6] [7]}Por el contrario, la dureza se conoce cuando los automorfismos están restringidos de cierta manera; por ejemplo, determinar la existencia de un automorfismo sin punto fijo (un automorfismo que no repara ningún vértice) es NP-completo, y el problema de contar dichos automorfismos es # P-completo. ^[5] [7]

Algoritmos, software y aplicaciones [ editar ]

Si bien no se conocen algoritmos de tiempo polinomial en el peor de los casos para el problema general del Automorfismo de gráficos, es bastante fácil encontrar el grupo de automorfismo (e imprimir un conjunto irredundante de generadores) para muchos gráficos grandes que surgen en las aplicaciones. Varias herramientas de software de código abierto están disponibles para esta tarea, incluyendo NAUTY , ^[8] BLISS ^[9] y SAUCY . ^[10] [11] SAUCY y BLISS son particularmente eficientes para gráficos dispersos, por ejemplo, SAUCY procesa algunos gráficos con millones de vértices en cuestión de segundos. Sin embargo, BLISS y NAUTY también pueden producir etiquetado canónico., mientras que SAUCY está actualmente optimizado para resolver Graph Automorphism. Una observación importante es que para un gráfico en n vértices, el grupo de automorfismo puede especificarse por no más de n-1 generadores, y los paquetes de software anteriores están garantizados para satisfacer este límite como un efecto secundario de sus algoritmos (conjuntos mínimos de los generadores son más difíciles de encontrar y no son particularmente útiles en la práctica). También parece que el soporte total (es decir, el número de vértices movidos) de todos los generadores está limitado por una función lineal de n , que es importante en el análisis de tiempo de ejecución de estos algoritmos. Sin embargo, esto no se ha establecido de hecho, a partir de marzo de 2012.

Las aplicaciones prácticas de Graph Automorphism incluyen dibujo de gráficos y otras tareas de visualización, resolviendo instancias estructuradas de satisfacción booleana que surgen en el contexto de la verificación formal y la logística . La simetría molecular puede predecir o explicar las propiedades químicas.

Pantalla de simetría [ editar ]

Varios investigadores de dibujo gráfico han investigado algoritmos para dibujar gráficos de tal manera que los automorfismos del gráfico se vuelvan visibles como simetrías del dibujo. Esto puede hacerse utilizando un método que no está diseñado alrededor de simetrías, pero que genera automáticamente dibujos simétricos cuando sea posible, ^[12] o identificando explícitamente simetrías y usándolas para guiar la colocación de vértices en el dibujo. ^[13] No siempre es posible mostrar todas las simetrías del gráfico simultáneamente, por lo que puede ser necesario elegir qué simetrías mostrar y cuáles dejar sin visualizar.

Graficar familias definidas por sus automorfismos [ editar ]

Varias familias de gráficos se definen por tener ciertos tipos de automorfismos:

• Un gráfico asimétrico es un gráfico no dirigido con solo el automorfismo trivial.
• Un gráfico transitivo de vértice es un gráfico no dirigido en el que cada vértice puede ser mapeado por un automorfismo en cualquier otro vértice.
• Un gráfico transitivo de borde es un gráfico no dirigido en el que cada borde puede ser mapeado por un automorfismo en cualquier otro borde.
• Un gráfico simétrico es un gráfico tal que cada par de vértices adyacentes puede ser mapeado por un automorfismo en cualquier otro par de vértices adyacentes.
• Un gráfico transitivo de distancia es un gráfico tal que cada par de vértices puede ser mapeado por un automorfismo en cualquier otro par de vértices que estén a la misma distancia.
• Un gráfico semi-simétrico es un gráfico transitivo de borde pero no transitivo de vértice.
• Un gráfico semitransitivo es un gráfico que es transitivo al vértice y transitivo al borde pero no simétrico.
• Un gráfico simétrico sesgado es un gráfico dirigido junto con una permutación σ en los vértices que asigna bordes a bordes pero invierte la dirección de cada borde. Además, se requiere que σ sea una involución .

Las relaciones de inclusión entre estas familias se indican en la siguiente tabla:

transitiva a distanciadistancia regularfuertemente regular

simétrico (arco transitivo)t -transitivo, t ≥ 2

(si está conectado)

vértice y borde transitivoborde transitivo y regularborde transitivo

vértice transitivoregular

Gráfico de Cayley

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Gráfico bipartito completo
Un gráfico bipartito completo con m = 5 yn = 3
Vértices	n + m
Bordes	Minnesota
Radio	{\ displaystyle \ left \ {{\ begin {array} {ll} 1 & m = 1 \ vee n = 1 \\ 2 & {\ text {else}} \ end {array}} \ right.}
Diámetro	{\ displaystyle \ left \ {{\ begin {array} {ll} 1 & m = n = 1 \\ 2 & {\ text {else}} \ end {array}} \ right.}
Circunferencia	{\ displaystyle \ left \ {{\ begin {array} {ll} \ infty & m = 1 \ vee n = 1 \\ 4 & {\ text {else}} \ end {array}} \ right.}
Automorfismos	{\ displaystyle \ left \ {{\ begin {array} {ll} 2m! n! & n = m \\ m! n! & {\ text {else}} \ end {array}} \ right.}
Número cromático	2
Índice cromático	max { m , n }
Espectro	$${\ displaystyle \ {0 ^ {n + m-2}, (\ pm {\ sqrt {nm}}) ^ {1} \}}
Notación	$${\ displaystyle K_ {m, n}}
Tabla de gráficos y parámetros.

En el campo matemático de la teoría de grafos , un gráfico bipartito completo o biclique es un tipo especial de gráfico bipartito donde cada vértice del primer conjunto está conectado a cada vértice del segundo conjunto. ^[1] [2]

La teoría de grafos en sí misma suele tener una fecha que comienza con el trabajo de Leonhard Euler de 1736 sobre los Siete Puentes de Königsberg . Sin embargo, ya se imprimieron dibujos de gráficos bipartitos completos ya en 1669, en relación con una edición de las obras de Ramon Llull editadas por Athanasius Kircher . ^[3] [4] Llull mismo había hecho dibujos similares de gráficos completos tres siglos antes.

Definición [ editar ]

Un gráfico bipartito completo es un gráfico cuyos vértices se pueden dividir en dos subconjuntos V ₁ y V _{2 de} modo que ningún borde tenga ambos extremos en el mismo subconjunto, y cada borde posible que pueda conectar vértices en diferentes subconjuntos es parte del gráfico. Es decir, es un gráfico bipartito ( V ₁ , V ₂ , E ) de modo que por cada dos vértices v ₁ ∈ V ₁ y v ₂ ∈ V ₂ , v ₁ v ₂ es un borde en E. Un gráfico bipartito completo con particiones de tamaño | V ₁ | = my | V ₂ | = n , se denota K _{m, n} ; ^[1] [2] cada dos gráficos con la misma notación son isomorfos .

Ejemplos [ editar ]

Los gráficos de estrellas K _1,3 , K _1,4 , K _1,5 y K _1,6 .

• Para cualquier k , K _1, k se llama estrella . ^[2] Todos los gráficos bipartitos completos que son árboles son estrellas.
• El gráfico K _1,3 se llama garra y se utiliza para definir los gráficos sin garras . ^[5]
• El gráfico K _3,3 se llama el gráfico de utilidad . Este uso proviene de un rompecabezas matemático estándar en el que tres servicios públicos deben estar conectados a tres edificios; es imposible de resolver sin cruces debido a la falta de planitud de K _3,3 . ^[6]

• Las bicliques máximas que se encuentran como subgrafías del digrafo de una relación se denominan conceptos . Cuando se forma un enrejado tomando encuentros y uniones de estos subgrafos, la relación tiene un enrejado de concepto inducido . Este tipo de análisis de relaciones se llama análisis conceptual formal .

Propiedades [ editar ]

Ejemplo K _p , p gráficos bipartitos completos ^[7]

K 3,3	K 4,4	K 5,5
3 colores de borde	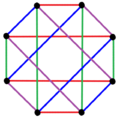4 colores de borde	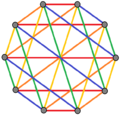5 colores de borde
Los polígonos complejos regulares de la forma 2 {4} p tienen gráficos bipartitos completos con 2 p vértices (rojo y azul) y p 2 2 bordes. También se pueden dibujar como colores de borde p .

• Dado un gráfico bipartito, probar si contiene un subgrafo bipartito completo K _i , i para un parámetro  i es un problema NP-completo . ^[8]
• Un gráfico plano no puede contener K _3,3 como menor ; un gráfico del plano externo no puede contener K _3,2 como un menor (Estas no son condiciones suficientes para la planaridad y la planitud externa, pero son necesarias). Por el contrario, cada gráfico no plano contiene K _3,3 o el gráfico completo K ₅ como menor; Este es el teorema de Wagner . ^[9]
• Cada gráfico bipartito completo. K _n , n es un gráfico de Moore y una jaula ( n , 4) . ^[10]
• El bipartito completa gráficos de K _n , n y K _n , n 1 tiene el máximo número posible de los bordes entre todos los gráficos libre de triángulo con el mismo número de vértices; Este es el teorema de Mantel . El resultado de Mantel se generalizó a gráficos k -partitos y gráficos que evitan camarillas más grandes como subgrafos en el teorema de Turán , y estos dos gráficos bipartitos completos son ejemplos de gráficos de Turán , los gráficos extremos para este problema más general. ^[11]
• El gráfico bipartito completo K _m , n tiene un número de vértices que cubren min { m , n } y un número de cobertura de borde de max { m , n }.
• El gráfico bipartito completo K _m , n tiene un conjunto independiente máximo de tamaño máximo { m , n }.
• La matriz de adyacencia de un gráfico bipartito completo K _m , n tiene valores propios √ nm , - √ nm y 0; con multiplicidad 1, 1 yn + m −2 respectivamente. ^[12]
• La matriz laplaciana de un gráfico bipartito completo K _m , n tiene valores propios n + m , n , m y 0; con multiplicidad 1, m −1, n −1 y 1 respectivamente.
• Un gráfico bipartito completo K _m , n tiene m ^n −1 n ^m −1 árboles de expansión . ^[13]
• Un gráfico bipartito completo K _m , n tiene una coincidencia máxima de tamaño min { m , n }.
• Un gráfico bipartito completo K _n , n tiene una coloración n -dege adecuada correspondiente a un cuadrado latino . ^[14]
• Cada gráfico bipartito completo es un gráfico modular : cada triple de vértices tiene una mediana que pertenece a los caminos más cortos entre cada par de vértices.