TEORÍA DE TÉRMINOS DE GRAFOS

complejo de cadena es una estructura algeb raica que consiste en una secuencia de grupos abelianos (o módulos ) y una secuencia de homomorfismos entre grupos consecutivos de modo que la imagen de cada homomorfismo se incluya en el núcleo del siguiente. Asociado a un complejo de cadena está su homología , que describe cómo se incluyen las imágenes en los núcleos.

Un complejo de cochain es similar a un complejo de cadena, excepto que sus homomorfismos siguen una convención diferente. La homología de un complejo cochain se llama cohomología.

En la topología algebraica , el complejo de cadena singular de un espacio topológico X se construye usando mapas continuos de un simplex a X, y los homomorfismos del complejo de la cadena capturan cómo estos mapas se restringen al límite del simplex. La homología de este complejo de cadena se llama homología singular de X, y es una invariante de un espacio topológico de uso común .

Los complejos de cadena se estudian en álgebra homológica , pero se usan en varias áreas de las matemáticas, incluyendo álgebra abstracta , teoría de Galois , geometría diferencial y geometría algebraica . Se pueden definir más generalmente en categorías abelianas .

Definiciones [ editar ]

Un complejo de cadena $${\ displaystyle (A _ {\ bullet}, d _ {\ bullet})}es una secuencia de grupos o módulos abelianos ..., A ₀ , A ₁ , A ₂ , A ₃ , A ₄ , ... conectados por homomorfismos (llamados operadores de límites o diferenciales ) d _n  : A _n → A _n −1 , de modo que la composición de dos mapas consecutivos sea el mapa cero. Explícitamente, los diferenciales satisfacen d _n ∘ d _n +1 = 0, o con índices suprimidos, d ² = 0. El complejo se puede escribir de la siguiente manera.

$${\ displaystyle \ cdots {\ xleftarrow {d_ {0}}} A_ {0} {\ xleftarrow {d_ {1}}} A_ {1} {\ xleftarrow {d_ {2}}} A_ {2} {\ xleftarrow {d_ {3}}} A_ {3} {\ xleftarrow {d_ {4}}} A_ {4} {\ xleftarrow {d_ {5}}} \ cdots}

El complejo cochain $${\ displaystyle (A ^ {\ bullet}, d ^ {\ bullet})}es la noción dual de un complejo de cadena. Consiste en una secuencia de grupos o módulos abelianos ..., A ⁰ , A ¹ , A ² , A ³ , A ⁴ , ... conectados por homomorfismos d ⁿ  : A ⁿ → A ^n +1 satisfactoria d ^n +1 ∘ d ⁿ = 0. El complejo de la cadena puede escribirse de manera similar al complejo de la cadena.

${\displaystyle \cdots {\xrightarrow {d^{-1}}}A^{0}{\xrightarrow {d^{0}}}A^{1}{\xrightarrow {d^{1}}}A^{2}{\xrightarrow {d^{2}}}A^{3}{\xrightarrow {d^{3}}}A^{4}{\xrightarrow {d^{4}}}\cdots }$

El índice n en A _n o A ⁿ se conoce como el grado (o dimensión ). La diferencia entre los complejos de cadena y cochain es que, en los complejos de cadena, los diferenciales disminuyen la dimensión, mientras que en los complejos de cochain aumentan la dimensión. Todos los conceptos y definiciones para complejos de cadena se aplican a los complejos de cochain, excepto que seguirán esta convención diferente para la dimensión, y a menudo los términos recibirán el prefijo co- . En este artículo, se darán definiciones para complejos de cadena cuando no se requiere la distinción.

Un complejo de cadena acotada es uno en el que casi todos los A _n son 0; es decir, un complejo finito extendido a la izquierda y a la derecha en 0. Un ejemplo es el complejo de cadena que define la homología simplicial de un complejo simplicial finito . Un complejo de cadena está limitado arriba si todos los módulos por encima de algún grado fijo N son 0, y está limitado por debajo si todos los módulos por debajo de algún grado fijo son 0. Claramente, un complejo está limitado tanto por encima como por debajo si y solo si el complejo está limitado.

Los elementos de los grupos individuales de un complejo de (co) cadenas se denominan (co) cadenas . Los elementos en el núcleo de d se denominan (co) ciclos (o elementos cerrados ), y los elementos en la imagen de d se denominan (co) límites (o elementos exactos ). Desde la definición del diferencial, todos los límites son ciclos. El n -ésimo grupo de (co) homología H _n ( H ⁿ ) es el grupo de (co) ciclos módulo (co) límites en grado n , es decir,

$${\ displaystyle H_ {n} = {\ frac {\ ker d_ {n}} {{\ mbox {im}} d_ {n + 1}}} \ quad \ left (H ^ {n} = {\ frac { \ ker d ^ {n}} {{\ mbox {im}} d ^ {n-1}}} \ right)}

Secuencias exactas [ editar ]

Artículo principal: secuencia exacta

Una secuencia exacta (o complejo exacto ) es un complejo de cadena cuyos grupos de homología son todos cero. Esto significa que todos los elementos cerrados en el complejo son exactos. Una secuencia exacta corta es una secuencia exacta acotada en la que solo los grupos A _k , A _k +1 , A _k +2 pueden ser distintos de cero. Por ejemplo, el siguiente complejo de cadena es una secuencia corta y exacta.

$${\ displaystyle \ cdots {\ xrightarrow {}} \; 0 \; {\ xrightarrow {}} \; \ mathbf {Z} \; {\ xrightarrow {\ times p}} \; \ mathbf {Z} \ twoheadrightarrow \ mathbf {Z} / p \ mathbf {Z} \; {\ xrightarrow {}} \; 0 \; {\ xrightarrow {}} \ cdots}

En el grupo intermedio, los elementos cerrados son los elementos p Z ; Estos son claramente los elementos exactos en este grupo.

Cadena de mapas [ editar ]

Un mapa de cadena f entre dos complejos de cadena$${\ displaystyle (A _ {\ bullet}, d_ {A, \ bullet})} y $${\ displaystyle (B _ {\ bullet}, d_ {B, \ bullet})} es una secuencia $${\ displaystyle f _ {\ bullet}} de homomorfismos $${\ displaystyle f_ {n}: A_ {n} \ rightarrow B_ {n}}para cada n que conmuta con los operadores de límite en los dos complejos de cadena, entonces$${\ displaystyle d_ {B, n} \ circ f_ {n} = f_ {n-1} \ circ d_ {A, n}}. Esto está escrito en el siguiente diagrama conmutativo .

Un mapa de cadena envía ciclos a ciclos y límites a límites, y por lo tanto induce un mapa de homología. $${\ displaystyle (f _ {\ bullet}) _ {*}: H _ {\ bullet} (A _ {\ bullet}, d_ {A, \ bullet}) \ rightarrow H _ {\ bullet} (B _ {\ bullet}, d_ {B, \ bullet})}.

Un mapa continuo f entre espacios topológicos X e Y induce un mapa de cadena entre los complejos de cadena singulares de X e Y , y por lo tanto induce un mapa f _* entre la homología singular de X e Y también. Cuando X e Y son iguales a la n- esfera , el mapa inducido en la homología define el grado del mapa f .

El concepto de mapa de cadena se reduce al de límite a través de la construcción del cono de un mapa de cadena.

Homotopía en cadena [ editar ]

Ver también: categoría de homotopía de complejos de cadena

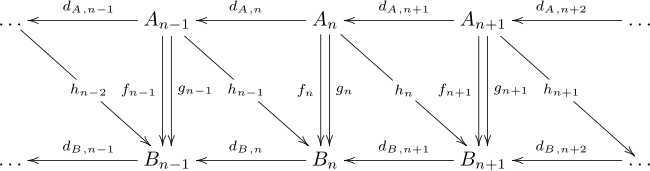
Una homotopía en cadena ofrece una manera de relacionar dos mapas en cadena que inducen el mismo mapa en grupos de homología, aunque los mapas pueden ser diferentes. Dados dos complejos de cadena A y B , y dos mapas de cadena f , g  : A → B , una homotopía de cadena es una secuencia de homomorfismos h _n  : A _n → B _n +1 tal que hd _A + d _B h = f - g . Los mapas se pueden escribir en un diagrama de la siguiente manera, pero este diagrama no es conmutativo.

El mapa hd _A + d _B h se verifica fácilmente para inducir el mapa cero en la homología, para cualquier h . Inmediatamente se deduce que f y g inducen el mismo mapa en la homología. Uno dice que f y g son homotópicas de cadena (o simplemente homotópicas ), y esta propiedad define una relación de equivalencia entre los mapas de cadena.

Deje X e Y ser espacios topológicos. En el caso de homología singular, una homotopía entre mapas continuos f , g  : X → Y induce una homotopía en cadena entre los mapas de cadena correspondientes a f y g . Esto muestra que dos mapas homotópicos inducen el mismo mapa en homología singular. El nombre "homotopía en cadena" está motivado por este ejemplo.

Ejemplos [ editar ]

Homología singular [ editar ]

Artículo principal: homología singular

Deje X ser un espacio topológico. Defina C _n ( X ) para que n natural sea ​​el grupo abeliano libre generado formalmente por n-simplices singulares en X , y defina el mapa de límites$${\ displaystyle \ partial _ {n}: C_ {n} (X) \ a C_ {n-1} (X)} ser - estar

$${\ displaystyle \ partial _ {n}: \, (\ sigma: [v_ {0}, \ ldots, v_ {n}] \ to X) \ mapsto \ sum _ {i = 0} ^ {n} (- 1) ^ {i} (\ sigma: [v_ {0}, \ ldots, {\ hat {v}} _ {i}, \ ldots, v_ {n}] \ a X)}

donde el sombrero denota la omisión de un vértice . Es decir, el límite de un simplex singular es la suma alterna de restricciones a sus caras. Se puede demostrar que ∂ ² = 0, entonces$${\ displaystyle (C _ {\ bullet}, \ partial _ {\ bullet})}es un complejo de cadena; la homología singular $${\ displaystyle H _ {\ bullet} (X)} Es la homología de este complejo.

La homología singular es una invariante útil de espacios topológicos hasta la equivalencia de homotopía . El grupo de homología de cero grados es un grupo abeliano libre en los componentes conectados de X .

de Rham cohomology [ editar ]

Artículo principal: cohomología de Rham

El diferencial k -formas en cualquier múltiple liso M forma un verdadero espacio de vector llamado Ω ^k ( M ) bajo adición. La derivada exterior d asigna Ω ^k ( M ) a Ω ^k +1 ( M ), y d ² = 0 se sigue esencialmente de la simetría de las segundas derivadas , por lo que los espacios vectoriales de las formas k junto con la derivada exterior son un complejo de cadena.

$${\ displaystyle \ Omega ^ {0} (M) \ {\ stackrel {d} {\ to}} \ \ Omega ^ {1} (M) \ to \ Omega ^ {2} (M) \ to \ Omega ^ {3} (M) \ a \ cdots}

La cohomología de este complejo se llama la cohomología de de Rham de X . El grupo de homología en cero dimensión es isomorfo al espacio vectorial de las funciones localmente constantes de M a R . Así, para un distribuidor compacto, este es el espacio vectorial real cuya dimensión es el número de componentes conectados de M .

Los mapas suaves entre múltiples inducen mapas de cadena, y las homotopías suaves entre mapas inducen homotopías de cadena.

Categoría de complejos de cadena [ editar ]

Los complejos de cadena de módulos K con mapas de cadena forman una categoría Ch _K , donde K es un anillo conmutativo.

Si V = V$${\ displaystyle {} _ {*}}y W = W$${\ displaystyle {} _ {*}}son complejos de cadena, su producto tensorial $${\ displaystyle V \ otimes W}es un complejo de cadena con elementos de grado n dados por

$${\ displaystyle (V \ otimes W) _ {n} = \ bigoplus _ {\ {i, j | i + j = n \}} V_ {i} \ otimes W_ {j}}

y diferencial dado por

$${\ displaystyle \ partial (a \ otimes b) = \ partial a \ otimes b + (- 1) ^ {\ left | a \ right |} a \ otimes \ partial b}

donde un y b son dos vectores homogéneas en V y W , respectivamente, y$${\ displaystyle \ left | a \ right |}denota el grado de a .

Este producto tensor convierte la categoría Ch _K en una categoría monoidal simétrica . El objeto de identidad con respecto a este producto monoidal es el anillo base K visto como un complejo de cadena en grado 0. El trenzado se da en tensores simples de elementos homogéneos por

$${\ displaystyle a \ otimes b \ mapsto (-1) ^ {\ left | a \ right | \ left | b \ right |} b \ otimes a}

El signo es necesario para que el trenzado sea un mapa en cadena.

Además, la categoría de complejos de cadena de módulos K también tiene Hom interno : los complejos de cadena dados V y W , el Hom interno de V y W , denominado Hom ( V , W ), es el complejo de cadena con elementos de grado n dados por$${\ displaystyle \ Pi _ {i} {\ text {Hom}} _ {K} (V_ {i}, W_ {i + n})} y diferencial dado por

$${\ displaystyle (\ partial f) (v) = \ partial (f (v)) - (- 1) ^ {\ left | f \ right |} f (\ partial (v))}.

Tenemos un isomorfismo natural.

$${\ displaystyle {\ text {Hom}} (A \ otimes B, C) \ cong {\ text {Hom}} (A, {\ text {Hom}} (B, C))}

De Wikipedia, la enciclopedia libre

Saltar a navegaciónSaltar a búsqueda

Un ciclo (negro) con dos acordes (verde). En cuanto a esta parte, el gráfico es cordal. Sin embargo, eliminar un borde verde daría como resultado un gráfico no cordal. De hecho, el otro borde verde con tres bordes negros formaría un ciclo de longitud cuatro sin acordes.

En el área matemática de la teoría de grafos , un gráfico cordal es uno en el que todos los ciclos de cuatro o más vértices tienen un acorde , que es un borde que no es parte del ciclo pero conecta dos vértices del ciclo. De manera equivalente, cada ciclo inducido en el gráfico debe tener exactamente tres vértices. Los gráficos cordales también pueden caracterizarse como los gráficos que tienen ordenamientos de eliminación perfectos, como los gráficos en los que cada separador mínimo es una camarilla, y como los gráficos de intersección de los subárboles de un árbol. A veces también se les llama gráficos de circuito rígido ^[1] o gráficos triangulados . ^[2]

Los gráficos cordales son un subconjunto de los gráficos perfectos . Pueden reconocerse en el tiempo polinómico , y varios problemas que son difíciles para otras clases de gráficos, como la coloración de gráficos, pueden resolverse en tiempo polinómico cuando la entrada es cordal. El ancho de árbol de un gráfico arbitrario puede caracterizarse por el tamaño de las camarillas en los gráficos cordales que lo contienen.

Eliminación perfecta y reconocimiento eficiente [ editar ]

Un ordenamiento de eliminación perfecto en un gráfico es un ordenamiento de los vértices del gráfico de tal manera que, para cada vértice v , v y los vecinos de v que ocurren después de v en el orden formen una camarilla . Un gráfico es cordal si y solo si tiene un orden de eliminación perfecto. ^[3]

Rose, Lueker y Tarjan (1976) (ver también Habib et al. 2000 ) muestran que un ordenamiento de eliminación perfecto de un gráfico cordal se puede encontrar eficientemente usando un algoritmo conocido como búsqueda lexicográfica de amplitud . Este algoritmo mantiene una partición de los vértices del gráfico en una secuencia de conjuntos; Inicialmente, esta secuencia consiste en un único conjunto con todos los vértices. El algoritmo elige repetidamente un vértice v del primer conjunto de la secuencia que contiene vértices previamente no elegidos, y divide cada conjunto S de la secuencia en dos subconjuntos más pequeños, el primero formado por los vecinos de v en Sy el segundo compuesto por los no vecinos. Cuando este proceso de división se ha realizado para todos los vértices, la secuencia de conjuntos tiene un vértice por conjunto, en el reverso de un orden de eliminación perfecto.

Dado que tanto este primer proceso de búsqueda de amplitud lexicográfica como el proceso de probar si un pedido es una eliminación perfecta se puede realizar en tiempo lineal, es posible reconocer gráficos cordales en tiempo lineal. El problema del sándwich gráfico en los gráficos cordales es NP-completo ^[4] mientras que el problema del gráfico de la sonda en los gráficos cordales tiene una complejidad de tiempo polinómico. ^[5]

El conjunto de todos los ordenamientos de eliminación perfectos de un gráfico cordal se puede modelar como las palabras básicas de un antimatroide ; Chandran y col. (2003) usan esta conexión con los antimatroides como parte de un algoritmo para enumerar de manera eficiente todos los ordenamientos de eliminación perfectos de un gráfico cordal dado.

Máximas camarillas y coloración gráfica [ editar ]

Otra aplicación de los ordenamientos de eliminación perfectos es encontrar una camarilla máxima de un gráfico cordal en tiempo polinómico, mientras que el mismo problema para los gráficos generales es NP-completo . En términos más generales, un gráfico cordal solo puede tener linealmente muchas camarillas máximas , mientras que los gráficos no cordales pueden tener exponencialmente muchos. Para enumerar todas las camarillas máximas de un gráfico cordal, simplemente encuentre un orden de eliminación perfecto, forme una camarilla para cada vértice v junto con los vecinos de v que sean posteriores a v en el orden de eliminación perfecto y pruebe si cada una de las camarillas resultantes es máximo.

Los gráficos de camarilla de los gráficos cordales son los gráficos doblemente cordales . ^[6]

La camarilla máxima más grande es una camarilla máxima y, como los gráficos cordales son perfectos, el tamaño de esta camarilla es igual al número cromático del gráfico cordal. Los gráficos cordales son perfectamente ordenables : se puede obtener un color óptimo aplicando un algoritmo de color codicioso a los vértices en el reverso de un orden de eliminación perfecto. ^[7]

El polinomio cromático de un gráfico cordal es fácil de calcular. Encuentra un pedido de eliminación perfecto$${\ displaystyle v_ {1}, v_ {2}, \ ldots, v_ {n}.} Sea N _i igual al número de vecinos de v _i que vienen después de v _i en ese orden. Por ejemplo, N _n  = 0. El polinomio cromático es igual a$${\ displaystyle (x-N_ {1}) (x-N_ {2}) \ cdots (x-N_ {n}).} (El último factor es simplemente x , entonces x divide el polinomio, como debería). Claramente, este cálculo depende de la cordalidad. ^[8]

Separadores mínimos [ editar ]

En cualquier gráfico, un separador de vértices es un conjunto de vértices cuya eliminación deja el gráfico restante desconectado; un separador es mínimo si no tiene un subconjunto adecuado que también sea un separador. Según un teorema de Dirac (1961) , los gráficos cordales son gráficos en los que cada separador mínimo es una camarilla; Dirac utilizó esta caracterización para demostrar que los gráficos cordales son perfectos .

La familia de gráficos cordales se puede definir inductivamente como los gráficos cuyos vértices se pueden dividir en tres subconjuntos no vacíos A , S y B , de modo que A  ∪  S y S  ∪  B forman subgrafos inducidos por el cordal , S es una camarilla, y allí hay bordes de a a B . Es decir, son los gráficos que tienen una descomposición recursiva por separadores de camarillas en subgrafías más pequeñas. Por esta razón, los gráficos cordales también se han llamado a veces gráficos descomponibles . ^[9]

Gráficos de intersección de subárboles [ editar ]

Un gráfico cordal con ocho vértices, representado como el gráfico de intersección de ocho subárboles de un árbol de seis nodos.

Una caracterización alternativa de gráficos cordales, debido a Gavril (1974) , involucra árboles y sus subárboles.

De una colección de subárboles de un árbol, se puede definir un gráfico de subárbol , que es un gráfico de intersección que tiene un vértice por subárbol y un borde que conecta dos subárboles que se superponen en uno o más nodos del árbol. Gavril mostró que los gráficos de subárbol son exactamente los gráficos cordales.

Una representación de un gráfico cordal como una intersección de subárboles forma una descomposición de árbol del gráfico, con un ancho de árbol igual a uno menor que el tamaño de la camarilla más grande en el gráfico; La descomposición del árbol de cualquier gráfico G puede verse de esta manera como una representación de G como un subgrafo de un gráfico cordal. La descomposición del árbol de un gráfico es también el árbol de unión del algoritmo del árbol de unión .

Relación con otras clases de grafos [ editar ]

Subclases [ editar ]

Los gráficos de intervalo son los gráficos de intersección de subárboles de gráficos de ruta , un caso especial de árboles. Por lo tanto, son una subfamilia de gráficos cordales.

Los gráficos divididos son gráficos que son tanto cordales como los complementos de los gráficos cordales. Bender, Richmond y Wormald (1985) demostraron que, en el límite a medida que n va al infinito, la fracción de gráficos cordales de n-vértices que se dividen se aproxima a uno.

Los gráficos ptolemaicos son gráficos que son tanto cordales como hereditarios de distancia . Los gráficos de cuasi-umbral son una subclase de gráficos ptolemaicos que son tanto cordales como cográficos . Los gráficos de bloque son otra subclase de gráficos Ptolemaicos en los que cada dos camarillas máximas tienen como máximo un vértice en común. Un tipo especial son los gráficos de molinos de viento , donde el vértice común es el mismo para cada par de camarillas.

Los gráficos fuertemente cordales son gráficos que son cordales y no contienen n- sol (para n  ≥ 3) como un subgrafo inducido. Aquí un n -Sun es un n -vertex cordal gráfico G junto con una colección de n grado de dos vértices, adyacente a los bordes de un ciclo de Hamilton en  G .

Los árboles K son gráficos cordales en los que todas las camarillas máximas y todos los separadores de camarillas máximas tienen el mismo tamaño. ^{[10] Las} redes apolíneas son gráficos planos máximos cordales, o 3 árboles planar equivalentes. ^[10] Los gráficos del plano exterior máximoson una subclase de 2 árboles y, por lo tanto, también son cordales.

Superclases [ editar ]

Los gráficos cordales son una subclase de los gráficos perfectos bien conocidos . Otros superclases de gráficos de cuerdas incluyen gráficos débilmente cordales, gráficos poli-ganar , gráficos impar-Free Hole, gráficos de forma gratuita, incluso hoyos y gráficos Meyniel . Los gráficos cordales son precisamente los gráficos que están libres de agujeros impares y pares libres (ver agujeros en la teoría de gráficos).

Cada gráfico cordal es un gráfico estrangulado , un gráfico en el que cada ciclo periférico es un triángulo, porque los ciclos periféricos son un caso especial de ciclos inducidos. Los gráficos estrangulados son gráficos que pueden formarse por sumas de camarillas de gráficos cordales y gráficos planos máximos. Por lo tanto, los gráficos estrangulados incluyen gráficos planos máximos . ^[11]

Terminaciones cordales y ancho de árbol [ editar ]

Artículo principal: terminación cordal

Si G es un gráfico arbitrario, una terminación cordal de G (o relleno mínimo ) es un gráfico cordal que contiene G como un subgrafo. La versión parametrizada de relleno mínimo es un parámetro fijo manejable y, además, tiene solución en tiempo subexponencial parametrizado. ^[12] [13] El ancho de árbol de G es uno menos que el número de vértices en una camarilla máxima de una terminación cordal elegida para minimizar este tamaño de camarilla. Los árboles kson los gráficos a los que no se pueden agregar bordes adicionales sin aumentar su ancho de árbol a un número mayor que  k . Por lo tanto, los k- árboles son sus propias terminaciones cordales, y forman una subclase de los gráficos cordales. Las terminaciones cordales también se pueden usar para caracterizar varias otras clases relacionadas de gráficos.