Figuras geométricas

Esponja de Menger

Esponja de Menger.

En matemáticas, la esponja de Menger (a veces llamada cubo de Menger o bien cubo o esponja de Menger-Sierpiński o de Sierpiński) es un conjunto fractaldescrito por primera vez en 1926 por Karl Menger¹ mientras exploraba el concepto de dimensión topológica.²

Al igual que la alfombra de Sierpinski constituye una generalización bidimensional del conjunto de Cantor, esta es una generalización tridimensional de ambos. Comparte con estos muchas de sus propiedades, siendo un conjunto compacto, no numerable y de medida de Lebesgue nula. Su dimensión dimensión fractal de Hausdorff es  La esponja tiene una superficie infinita y al mismo tiempo encierra un volumen cero.

Es de destacar su propiedad de curva universal, pues es un conjunto topológico dedimensión topológica uno, y cualquier otra curva o grafo es homeomorfo a un subconjunto de la esponja de Menger.

La construcción de la esponja de Menger se define de forma recursiva:

1. Comenzamos con un cubo (primera imagen).
2. Dividimos cada cara del cubo en 9 cuadrados. Esto subdivide el cubo en 27 cubos más pequeños, como le sucede al cubo de Rubik.
3. Eliminamos los cubos centrales de cada cara (6) y el cubo central (1), dejando solamente 20 cubos (segunda imagen).
4. Repetimos los pasos 1, 2 y 3 para cada uno de los veinte cubos menores restantes.

La esponja de Menger es el límite de este proceso tras un número infinito de iteraciones.

 figuras de Lichtenberg (Lichtenberg-Figuren, o Lichtenberg Dust Figures) son imágenes producidas por descargas eléctricas ramificadas, arborescentes, que a veces se forman sobre la superficie o en el interior de materiales aislantes (dieléctricos).¹ Se llaman así por el físico alemán Georg Christoph Lichtenberg, quien inicialmente las descubrió y las estudió.¹ Al comienzo él pensó que esas formas características podrían ayudar a revelar la naturaleza de los "fluidos" eléctricos positivo y negativo, como se imaginaba la electricidad en esa época.² En 1777 Lichtenberg construyó un gran electróforo capaz de generar altastensiones de electricidad estática mediante un proceso de inducción eléctrica. Después de producir una descarga de alta tensión sobre un punto de la superficie de un material aislante, Lichtenberg hacía visibles los patrones radiales arborescentes mediante polvos coloreados que se fijaban sobre las cargas electrostáticas. Luego presionaba hojas de papel en blanco sobre las figuras ramificadas, lo que las transfería al papel y le permitía conservarlas. Así descubrió el principio básico que luego se emplearía en lasfotocopiadoras e impresoras por xerografía.³ Este descubrimiento también fue el inicio de la actual Física del plasma.- ..........................................:https://es.wikipedia.org/w/index.php?title=Figuras_de_Lichtenberg&printable=yes

Folium de Descartes

Folium de Descartes
x³ + y³ − 3axy = 0, a = 1.

El folium de Descartes (‘hoja de Descartes’) es una curva algebraica propuesta por vez primera por Descartes en 1638 con la ecuación implícita:

Que también puede ser descrita explícitamente en coordenadas polares como:

Ecuación de la tangente

Usando el método de diferenciación implícita, la ecuación anterior puede resolverse para y':

Usando la forma punto-pendiente de la ecuación de una línea, puede hallarse una ecuación para la tangente de la curva en :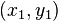

Tangentes horizontal y vertical

La línea tangente del folium de Descartes es horizontal cuando . Por tanto, la línea tangente es horizontal cuando:

La línea tangente del folium de Descartes es vertical cuando . Por tanto, la línea tangente es vertical cuando:

Esto puede explicarse gracias a una propiedad de la simetría de la curva. Mirando el gráfico, puede verse que la curva tiene dos tangentes horizontales y dos tangentes verticales. Así pues, la curva del folium de Descartes es simétrica respecto a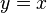 , por lo que si una tangente horizontal tiene una coordinada de 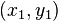, entonces hay una tangente vertical correspondiente, .