Figuras geométricas

Lagos de Wada

Los lagos de Wada

Atractor de x³ − 1 = 0;con la propiedad de Wada: los tres abiertos comparten la misma frontera. A diferencia de los lagos de Wada, cada uno de estos abiertos es disconexo.

Imaginemos un mapa con tres países (representados por abiertos arcoconexos). Pensemos en la frontera de estos países. Habrá puntos de la misma que sean frontera de dos de ellos, y puede que haya alguno que sea frontera de los tres simultáneamente. La intuición puede hacernos creer que el número de estos últimos puntos debe ser escaso, pero el contraejemplo conocido como los lagos de Wada nos muestra que esto no es así.

En matemáticas, los lagos de Wada son una construcción formada por tres abiertos conexosdisjuntos del plano con una frontera común a los tres. Esta construcción fue publicada por el matemático japonés Kunizō Yoneyama en 1917, que la nombró así en honor a su profesorTakeo Wada. Este descubrimiento se realizó de forma independiente al del matemático holandés Brouwer, que en 1910 halló un ejemplo similar.

De los conjuntos que comparten una propiedad similar se dicen que tienen la propiedad de Wada. Entre los ejemplos de los mismos aparecen atractores de sistemas dinámicos.

La construcción formal de los lagos de Wada puede iniciarse con el interior de un cuadrado de lado unidad, al que llamaremos tierra firme. En él cavaremos tres lagos (numerados como 0, 1 y 2 ) que iremos extendiendo en días sucesivos siguiendo la siguiente regla:

• Sea a_n una sucesión que converja a cero. En el día n = 1, 2, 3, 4, ... extenderemos el lago n mod 3 (= 1, 2, 0, 1...) de modo que pase a una distancia a_n de la tierra firme restante.

Esto puede realizarse de modo que la tierra firme conserve su interior conexo, y cada lago siga siendo abierto. En el límite, tras un número infinito de pasos, los tres lagos continuarán siendo abiertos conexos y disjuntos, y la tierra firme restante se convertirá en la frontera común a todos ellos.

Esta construcción puede generalizarse a cualquier número finito k de lagos sustituyendo el orden en que los extendemos, originalmente de 1, 2, 0, 1, 2, 0, 1, 2, 0, ...., por 1, 2, ..., k-1, 0, 1, 2,..., k-1,0,... . Puede incluso generalizarse a un conjunto infinito numerable de lagos siguiendo el orden marcado por 0, 0, 1, 0, 1, 2, 0, 1, 2, 3, 0, 1, 2, 3, 4, ... .

Vuelo de Lévy

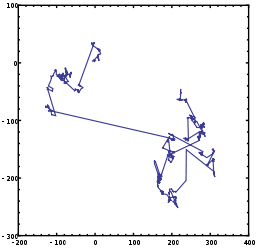
Un vuelo de Lévy, nombrado en honor al matemático francés Paul Pierre Lévy, es un tipo de paseo aleatorio en el cual los incrementos son distribuidos de acuerdo a una distribución de probabilidad de cola pesada. Específicamente, la distribución usada es una ley potencial de la forma y = x ^-a donde 1 < a < 3 y por lo tanto tiene una varianza infinita.

Los vuelos de Lévy son procesos de Márkov. Después de un gran número de pasos, la distancia del origen de la caminata al azar tiende a una distribución estable.

Los vuelos de Lévy de dos dimensiones fueron descritos por Benoît Mandelbrot en su libro The Fractal Geometry of Nature (La geometría fractal de la naturaleza). El escalamiento en forma de ley de potencias de las longitudes de pasos, da a los vuelos de Lévy una propiedad de escala invariante, es decir, la propiedad de un fractal.

Este método de simulación proviene fuertemente de las matemáticas relacionadas con la teoría del caos y es útil en la medida y las simulaciones estocásticas para los fenómenos naturales al azar o pseudoaleatorios. Los ejemplos incluyen análisis de datos deterremotos, matemáticas financieras, la criptografía, el análisis de señales así como muchas aplicaciones en astronomía, la biología, y lafísica.

Cuando los tiburones y otros depredadores del océano no pueden encontrar alimento, abandonan el movimiento browniano, el movimiento al azar visto en moléculas de gas, por el vuelo de Lévy —una mezcla de trayectorias largas y movimientos al azar cortos encontrados en líquidos turbulentos—. Los investigadores analizaron más de 12 millones de movimientos registrados durante 5.700 días en 55 animales marcados con un radio transmisor de 14 especies depredadoras del océano en los Océanos Atlánticos y Pacífico, incluyendo tiburones sedosos, atún de aleta amarilla, aguja azul y pez espada. Los datos mostraron que los vuelos de Lévy entremezclados con el movimiento browniano pueden describir los patrones de caza de los animales.^1 2

Cuadro 1. Un ejemplo de 1000 pasos de un vuelo de Lévy en dos dimensiones. El origen del movimiento está en [0.0], la dirección angular se distribuye uniformemente y el tamaño de paso está distribuido de acuerdo a la distribución de Lévy (es decir estable) con a=1 y ß=0 (es decir una distribución de Cauchy). Observe la presencia de saltos grandes en la localización comparada al movimiento browniano ilustrado en el cuadro 2.

Cuadro 2. Un ejemplo de 1000 pasos de una aproximación a un tipo de movimiento browniano de vuelo de Lévy en dos dimensiones. El origen del movimiento está en [0, 0], la dirección angular está distribuida uniformemente y el tamaño del paso está distribuido según una distribución de Lévy (es decir estable) con a=2 y ß=0 (es decir un de distribución normal).

Plano de Sorgenfrey

En el ámbito de la topología, el plano de Sorgenfrey a menudo es mencionado como un contraejemplo de muchas conjeturas que parecerían plausibles. El mismo consiste del producto de dos copias de la línea de Sorgenfrey, que es la línea real  bajo el intervalo topológico semiabierto. La línea y el plano de Sorgenfrey han sido nombrados en honor al matemático estadounidense Robert Sorgenfrey.

Una base del plano de Sorgenfrey, expresada como , es por lo tanto el grupo de rectángulos que incluyen el borde oeste, el vértice suroeste, y el borde sur, y omiten el vértice sureste, el borde este, el vértice noreste, el borde norte, y el vértice noroeste. Los conjuntos abiertos en  son uniones de estos rectángulos.