Figuras geométricas

Esferas de Dandelin

Las esferas de Dandelin G1 y G2 tocan al planoπ que se interseca con el cono en F1 y F2respectivamente, cayendo siempre estos puntos en la zona (azul claro) interior al cono.

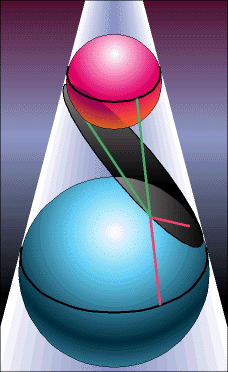
En geometría, a las curvas formadas por la intersección (no degenerada) de un plano con un cono se les llama secciones cónicas. Siempre existen uno o dos esferas interiores al cono que son simultáneamente tangentes al plano y al cono, estas son las denominadas esferas de Dandelin. El punto en el que cada una de estas esferas toca al plano es un foco de la sección cónica. A veces también son llamadas esferas focales.- ..........................................................:https://es.wikipedia.org/w/index.php?title=Esferas_de_Dandelin&printable=yes

espacio euclídeo es un tipo de espacio geométrico donde se satisfacen los axiomas de Euclides de la geometría. La recta real, elplano euclídeo y el espacio tridimensional de la geometría euclidiana son casos especiales de espacios euclídeos de dimensiones 1, 2 y 3 respectivamente. El concepto abstracto de espacio euclídeo generaliza esas construcciones a más dimensiones. Un espacio euclídeo es un espacio vectorial completo dotado de un producto interno (lo cual lo convierte además en un espacio normado, un espacio métricoy una variedad riemanniana al mismo tiempo).- ...................................:https://es.wikipedia.org/w/index.php?title=Espacio_eucl%C3%ADdeo&printable=yes