bruja de Agnesi (pronunciado 'Añesi'), también llamada la Hechicera de Agnesi o la Bruja de Maria Agnesi(nombrada así por Maria Agnesi) es la curva definida por lo siguiente:
 |
| Generación de la curva. |
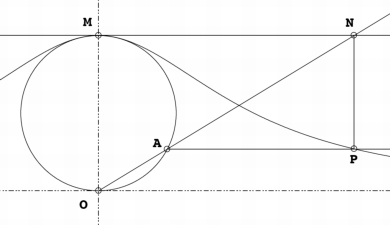
A partir de una circunferencia, y un punto cualquiera O de la circunferencia, siendo T el punto diametralmente opuesto a O. Para cualquier otro punto A de la circunferencia, la prolongación de la línea secante OA corta a la perpendicular a OT que pasa por T en B. La línea paralela a OT que pasa porB, y la línea perpendicular a OT que pasa por A se cortan en P. Tomando como variable el punto A se define que la curva de los puntos P es el de bruja.
La asíntota de esta curva es la línea tangente a la circunferencia que pasa por el punto O.- ...............:https://es.wikipedia.org/w/index.php?title=Bruja_de_Agnesi&printable=yes
Campila de Eudoxo
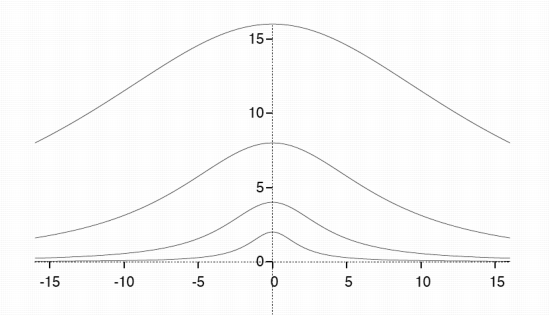
La campila de Eudoxo (en griego καμπύλη: curva) es una curva determinada por una ecuación cartesiana:
de la cual se ha de excluir la solución x = y = 0, o, en coordenadas polares:
El astrónomo y matemático griego Eudoxo de Cnido (c. 408 a. C. - c. 347 a. C.) estudió esta curva cuártica en relación con el problema clásico de la duplicación del cubo.
La campila es simétrica con respecto a ambos ejes: 
y 
. Corta el eje en 
y en 
. Tiene cuatro puntos de inflexión, en:
y . Corta el eje en y en . Tiene cuatro puntos de inflexión, en:
(uno en cada cuadrante). La primera mitad de la curva es asintótica a 
cuando 
. En efecto se puede escribir así:
cuando . En efecto se puede escribir así:
donde
es el 
ésimo número de Catalan.
ésimo número de Catalan.Caracol de Pascal
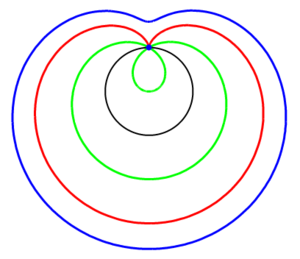
El caracol o "limaçon" de Pascal es la concoide de una circunferencia que pase por el polo. Es un tipo de epitrocoide.
Por tanto, su ecuación en coordenadas polares es:
En el caso particular de h=2·a, se obtiene una cardioide:
No hay comentarios:
Publicar un comentario