domingo, 6 de septiembre de 2015

Figuras geométricas

 círculo de Ford es un círculo centrado en \left(\frac p q , \frac1{2q^2}\right) y con radio \frac1{2q^2}, donde \frac p q  es una fracción irreducible, es decir, p y q son números enteros primos entre sí.
El círculo de Ford asociado a la fracción p/q se denota como C[p/q] o C[p, q]. Existe un círculo de Ford asociado a cualquier número racional. Es más, se puede considerar que la recta y = 1 es un círculo de Ford, concretamente el asociado con el infinito, el caso en quep = 1 y q = 0.
Dos círculos de Ford distintos son, o bien disjuntos o bien tangentes entre sí, pero el interior de un círculo de Ford no puede intersecar con el interior de otro círculo de Ford a pesar de que haya un círculo de Ford tangente al eje horizontal en cada uno de sus puntos de coordenada racional. Si p/q está entre 0 y 1, los círculos de Ford que son tangentes a C[p/q] son precisamente aquellos que están asociados con las fracciones que son la anterior o posterior a p/q en una sucesión de Farey determinada.
También se puede pensar en los círculos de Ford como curvas en el plano complejo. El grupo modular Gamma de transformaciones del plano complejo lleva círculos de Ford a otros círculos de Ford.
Interpretando la mitad superior del plano complejo como un modelo del plano hiperbólico (el modelo de semiplano de Poincaré), los círculos de Ford también se pueden interpretar como una teselación del plano hiperbólico mediante horociclos. Dos círculos de Ford cualesquiera son congruentes en la geometría hiperbólica. Si C[p/q] y C[r/s] son círculos de Ford tangentes entre sí, entonces el semicírculo que une (p/q, 0) con (r/s, 0) que es perpendicular con el eje x es una recta hiperbólica que también pasa por el punto donde los dos círculos son tangentes entre sí.
Los círculos de Ford son un subconjunto de los círculos presentes en el círculo de Apolonio generado por las rectas y = 0 e y = 1 y el círculo C[0/1].
Existe una relación entre el área total de los círculos de Ford, la función φ de Euler y la función zeta de Riemann.
Como ningún círculo de Ford interseca a ningún otro, se sigue inmediatamente que el área total de los círculos de Ford,
\left\{ C[p,q]: 0 \le \frac{p}{q} < 1 \right\},
es menor que 1. De hecho, el área total se puede expresar por una suma convergente que puede ser evaluada.
Aplicando la definición, el área es igual a:
A = \sum_{q\ge 1} \sum_{ (p, q)=1 \atop 1 \le p < q } \pi \left( \frac{1}{2 q^2} \right)^2.
Al simplificar esta expresión, se obtiene:
A = \frac{\pi}{4} \sum_{q\ge 1} \frac{1}{q^4} \sum_{ (p, q)=1 \atop 1 \le p < q } 1 = \frac{\pi}{4} \sum_{q\ge 1} \frac{\varphi(q)}{q^4} = \frac{\pi}{4} \frac{\zeta(3)}{\zeta(4)},
donde la última igualdad refleja la función generatriz de Dirichlet de φ(q). Como ζ(4) = π 4/90, se obtiene:
A = \frac{45}{2} \frac{\zeta(3)}{\pi^3}\approx 0.872284041.
Esta suma fue comentada en el grupo de noticias es.ciencia.matematicas.

Círculos de Ford. Cada uno de estos círculos se apoya sobre un número racional - una fracción. Los círculos oscuros corresponden a las fracciones 0/1, 1/1, 1/2, 1/3, 2/3, 1/4, 3/4, 1/5, 2/5, 3/5 y 4/5. Cada círculo estangente a la recta real y a los círculos vecinos. Las fracciones irreducibles con el mismo denominador tendrán círculos del mismo tamaño.





Concoide de Nicomedes

Conchoid of Nicomedes.png
La concoide de Nicomedes es la concoide de la recta, llamada "base".
Se pondrá la base perpendicular al eje polar, a una distancia b del polo y el radio de la circunferencia será h. Entonces, la ecuación de la concoide de Nicomedes es
\rho=\frac{b}{cos\ \omega} + h
que, en coordenadas cartesianas, queda:
(x-b)^2(x^2+y^2)=h^2 x^2 \,










Conjunto de Julia

Conjunto de Julia, un fractal. C = [0.285, -0.01].
Los conjuntos de Julia, así llamados por el matemático Gaston Julia, son una familia de conjuntos fractales que se obtienen al estudiar el comportamiento de los números complejos al ser iterados por una función holomorfa.
El conjunto de Julia de una función holomorfa f\, está constituido por aquellos puntos que bajo la iteración de f\, tienen un comportamiento 'caótico'. El conjunto se denota J(f)\,.
En el otro extremo se encuentra el conjunto de Fatou (en honor del matemático Pierre Fatou), que consiste de los puntos que tienen un comportamiento 'estable' al ser iterados. El conjunto de Fatou de una función holomorfa f\, se denota F(f)\, y es el complemento de J(f)\,.






Una familia muy notable de conjuntos de Julia se obtienen a partir de funciones cuadráticas simples: f_c(z) = z^2 + c\,, donde c\, es un número complejo. El conjunto de Julia que se obtiene a partir de esta función se denota J_c\,.
Un algoritmo para obtener el conjunto de Julia de f_c(z) = z^2 + c\, es el siguiente:
Para todo complejo z\, se construye por la siguiente sucesión:
z_0 = z\,
z_{n+1} = z_n^2 + c
Si esta sucesión queda acotada, entonces se dice que z\, pertenece al conjunto de Julia de parámetro c\,, denotado por J_c\,; de lo contrario,z\, queda excluido de éste.
En las imágenes anteriores, los puntos negros pertenecen al conjunto y los de color no. Los colores dan una indicación de la velocidad con la que diverge la sucesión (su módulo tiende a infinito): en rojo oscuro, al cabo de pocos cálculos se sabe que el punto no está en el conjunto; y en blanco, se ha tardado mucho más en comprobarlo. Como no se pueden calcular infinitos valores, es preciso poner un límite, y decidir que si los n\, primeros términos de la sucesión están acotados, el punto pertenece al conjunto. Al aumentar el valor de n\,se mejora la precisión de la imagen.
Conjunto de Julia en 3D.
Se puede demostrar que si |z_n| > 2\, entonces la sucesión diverge y el punto z no pertenece al conjunto de Julia. Por lo tanto, basta encontrar un solo término de la sucesión que verifique |z_n| > 2\, para tener la certeza de que z\, no está en el conjunto.
Existe una relación muy fuerte entre los conjuntos de Julia y el conjunto de Mandelbrot denotado por M\,, debido a la similitud de sus definiciones:
Se dice que c\, pertenece a M\, si y sólo si J_c\, es conexo.
Los resultados más vistosos se obtienen al tomar el parámetro c\, en la frontera de M\,, pues si c\,esta en el interior de M\, resulta que J_c\, toma el aspecto de un objeto redondo, poco fractal, y sólo el borde tiene la apariencia de fractal. Por ejemplo si c = 0 resulta que el conjunto de Julia es la circunferencia unitaria, con centro en el origen de coordenadas.
En las imágenes, se han tomado como valores de c: -1,3 + 0,00525·i; -0,72 – 0,196·i; -0,1 + 0,87·i y -0,51 – 0,601·i, por razones estéticas.
Se pueden generalizar estos conjuntos tomando otras relaciones de inducción: z_{n+1} = f(z_n)\, con cualquier función compleja f\,. Se puede también generalizar a cualquier dimensión, y emplear varias funciones en lugar de una sola.
Publicado por en

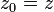
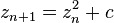
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)