Figuras geométricas

Sólidos de Catalan

El Hexaquisicosaedro, disdiaquistriacontaedro, icosaedro hexakis otriacontaedro disdiakis es uno de los sólidos de Catalan, cuyo dual es elicosidodecaedro truncado.

Los lados del triángulo que forman sus caras miden:

Siendo R el radio de la esfera que lo inscribe.

Al igual que el Hexaquisoctaedro se considera de caras uniformes ya que una es la inversión de la otra.

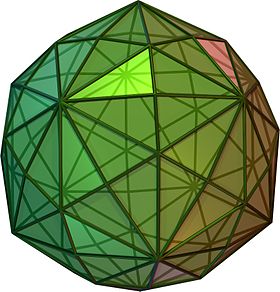Imagen del sólido
Caras	120
Polígonos que forman las caras	triángulos escalenos
Aristas	180
Vértices	62
Configuración de los vértices	30 de orden 6 20 de orden 4 12 de orden 10 En serie: 4, 6, 10
Grupo de simetría	Icosaédrico (Ih)
Poliedro dual	Icosidodecaedro truncado

El Hexaquisoctaedro, Disdiaquisdodecaedro, Dodecaedro Disdiakis u Octaedro Hexakis es uno de los sólidos de Catalan, cuyo dual es el cuboctaedro truncado. Se considera de caras uniformes aunque en realidad lo forman dos tipos de caras dado que en realidad una es la inversión de la otra. Este cuerpo puede ser considerado como un rombododecaedro al que se le han colocado pirámides bajas con la base en forma de rombo.

Imagen del sólido
Caras	48
Polígonos que forman las caras	Triángulos Escalenos
Aristas	72
Vértices	26
Configuración de los vértices	12 de orden 4 8 de orden 6 6 de orden 8 En serie: 4, 6, 8
Grupo de simetría	Octaédrico (Oh)
Poliedro dual	Cuboctaedro truncado

El hexecontaedro deltoidal o hexecontaedro trapezoidal es uno de los sólidos de Catalan cuyo dual es el rombicosidodecaedro que es un dodecaedro truncadomediante operaciones de truncamiento del poliedro uniforme. Y se asemeja a undodecaedro con las caras infladas o a un icosaedro con las caras infladas.

Imagen del sólido
Caras	60
Polígonos que forman las caras	Deltoides
Aristas	120
Vértices	62
Configuración de los vértices	12 de orden 5 20 de orden 3 30 de orden 4 En serie 3, 4, 5, 4
Grupo de simetría	Icosaédrico (Ih)
Poliedro dual	rombicosidodecaedro

El hexecontaedro pentagonal es uno de los sólidos de Catalan; su dual es elicosidodecaedro romo y es uno de los dos de esta familia que tiene un sólido isomórfico. Tiene dos vértices de orden 3 según los ángulos relacionados.

Hexecontaedro pentagonal
Familia: Sólidos de Catalan
Imagen del sólido
Sólido isomórfico
Caras	60
Polígonos que forman las caras	pentágonos irregulares
Aristas	150
Vértices	92
Configuración de los vértices	20 de orden 3 60 de orden 6 12 de orden 5 En serie: 3*, 3*, 3, 3*, 5
Grupo de simetría	Icosaédrico (I)
Poliedro dual	icosidodecaedro romo
Propiedades
Poliedro convexo de caras uniformes
Plano

El icositetraedro deltoidal o icositetraedro trapezoidal es uno de los sólidos de Catalan. Tiene dos vértices distintos de orden 4 según la forma en que se reúnen las caras que resultan unidas en cada uno; esta característica se repite en el icositetraedro pentagonal y en el hexecontaedro pentagonal.

Imagen del sólido
Caras	24
Polígonos que forman las caras	deltoides
Aristas	48
Vértices	26
Configuración de los vértices	8 de orden 3 6 de orden 4 6 de orden 4* En serie: 3, 4, 4*, 4
Grupo de simetría	Octaédrico (Oh)
Poliedro dual	Rombicuboctaedro

El icositetraedro pentagonal es uno de los sólidos de Catalan, cuyo dual es el cubo romo y es uno de los dos sólidos de Catalan que tiene una figura isomórfica; es decir, una figura de espejo dependiendo de la series de caras que se reúnen en los vértices. Además tiene dos tipos de vértices de orden 3 según los ángulos del pentágono que se encuentren en cada uno.

Icositetraedro pentagonal
Familia: Sólidos de Catalan
Imagen del sólido
Sólido isomórfico
Caras	24
Polígonos que forman las caras	pentágonos irregulares
Aristas	60
Vértices	38
Configuración de los vértices	6 de orden 4 8 de orden 3 24 de orden 3* En serie: 3*, 3*, 3, 3*, 4
Grupo de simetría	Octaédrico (O)
Poliedro dual	Cubo romo

Explicación de los vértices.