Mecánica

campo gravitatorio o campo gravitacional es un campo de fuerzas que representa la gravedad. Si se dispone en cierta región del espacio una masa M, el espacio alrededor de M adquiere ciertas características que no disponía cuando no estaba M. Este hecho se puede comprobar acercando otra masa m y constatando que se produce la interacción. A la situación física que produce la masa M se la denomina campo gravitatorio. Afirmar que existe algo alrededor de M es puramente especulativo, ya que sólo se nota el campo cuando se coloca la otra masa m, a la que se llama masa testigo. El tratamiento que recibe este campo es diferente según las necesidades del problema:

• En física newtoniana o física no-relativista el campo gravitatorio viene dado por un campo vectorial.
• En física relativista, el campo gravitatorio viene dado por un campo tensorial de segundo orden.- .......................................................................:https://es.wikipedia.org/w/index.php?title=Campo_gravitatorio&printable=yes

En la Física moderna interpretamos el campo gravitatorio como una alteración de las propiedades del espacio alrededor de los cuerpos. Esta alteración se mide por medio de la intensidad de campo, definida como la fuerza que experimenta la unidad de masa en un punto del campo. Así la intensidad de la gravedad cerca de la superficie de la Tierra vale aproximadamente 9,8N/kg y es un vector dirigido hacia el centro de la Tierra

El vector g de la figura nos mide la intensidad de la gravedad que crea un cuerpo de masa M en un punto exterior P a distancia R. El vector unitario uindica la dirección de la intensidad. Pulsando avanzar podrás ver gráficamente el campo creado por un cuerpo y el efecto de superposición que se produce cuando hay más de un cuerpo. En física el campo gravitatorio o campo gravitacional es un campo de fuerzas que representa la fuerza gravitatoria. El tratamiento que recibe este campo es diferente según las necesidades del problema: En física clásica o física no-relativista el campo gravitatorio viene dado por un campo vectorial. En física newtoniana, el campo gravitatorio es un campo vectorial conservativo cuyas líneas de campo son abiertas. Puede definirse como la fuerza por unidad de masa que experimentará una partícula puntual situada ante la presencia de una distribución de masa. Sus unidades son, por lo tanto, las de una aceleración, m s-2. Matemáticamente se puede definir el campo como donde 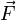 es la fuerza de gravedad experimentada por la partícula de masa  en presencia de un campo 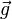. Lineas de campo gravitatorio de una masa. El campo  para una distribución de masa esférica y central fuera de la esfera es un vector de módulo g, dirección radial y que apunta hacia la partícula que crea el campo. , donde r es la distancia radial al centro de la distribución. En el interior de la esfera central el campo varía según una ley dependiente de la distribución de masa (para una esfera uniforme, crece linealmente desde el centro hasta el radio exterior de la esfera). La ecuación (1) por tanto sólo es válida a partir de la superficie exterior que limita el cuerpo que provoca el campo, punto a partir del cual el campo decrece según la ley de la inversa del cuadrado. El interés de realizar una descripción de la interacción gravitatoria ( Fuerza Gravitacional) por medio de un campo radica en la posibilidad de poder expresar la interacción gravitacional como el producto de dos términos, uno que depende del valor local del campo,  y otro, una propiedad escalar que representa la respuesta del objeto que sufre la acción del campo. Ejemplo: el movimiento de un planeta se puede describir como el movimiento orbital del planeta en presencia de un campo gravitatorio creado por el Sol. Los campos gravitatorios son aditivos. Es decir el campo gravitatorio creado por una distribución de masa es igual a la suma de los campos creados por sus diferentes elementos. El campo gravitatorio del sistema solar es el creado por el Sol, Júpiter y los demás planetas. La naturaleza conservativa del campo permite definir una energía potencial gravitatoria tal que la suma de la energía potencial y energía cinética del sistema es una cantidad constante. Así a cada punto del espacio podemos asignar un potencial Φ gravitatorio relacionado con la densidad de la distribición de masa y con el vector de campo gravitorio por:   El cardán (en España pronunciado cardan) es un componente mecánico, descrito por primera vez por Girolamo Cardano, que permite unir dos ejes no colineales. Su objetivo es transmitir el movimiento de rotación de un eje al otro a pesar de la no colinealidad. En los vehículos de motor se suele utilizar como parte del árbol de transmisión, que lleva la fuerza desde el motor situado en la parte delantera del vehículo hacia las ruedas traseras. El principal problema que genera el cardán es que, por su configuración, el eje al que se le transmite el movimiento no gira a unavelocidad angular constante. No obstante, si se colocan dos en serie y el principio y el final del árbol total se encuentran paralelos (como es el caso general de los vehículos de tracción trasera), estas diferencias se anulan. En la actualidad, la configuración más común en los automóviles es el motor delantero transversal con tracción delantera. En esta configuración, así como en otras en que el motor se ubica cerca de las ruedas motrices, no se utiliza el cardán. En estos casos la fuerza se transmite típicamente mediante semiejes y juntas homocinéticas. El cardán es fácilmente observable en camiones por su tamaño abultado, en los que el árbol de transmisión se observa como una larga pieza de metal que rota sobre sí misma cuando el vehículo está en marcha. Está ubicada longitudinalmente entre el motor y el tren trasero donde están montadas las ruedas, pudiéndose observar un cardán típicamente en el acople con eldiferencial o a la salida de la caja de cambios. El cardán se compone de tres partes principales: los rodillos, las horquillas y la cruceta. En música, también se llama cardán al eje que une los dos pedales del bombo de una batería. Centro de masas El centro de masas de un sistema discreto o continuo es el punto geométrico que dinámicamente se comporta como si en él estuviera aplicada la resultante de las fuerzas externas al sistema. De manera análoga, se puede decir que el sistema formado por toda la masaconcentrada en el centro de masas es un sistema equivalente al original. Normalmente se abrevia como c.m..- ............................................:https://es.wikipedia.org/w/index.php?title=Centro_de_masas&printable=yes Centro de masas El centro de masas de un sistema de partículas es un punto que, a muchos efectos, se mueve como si fuera una partícula de masa igual a la masa total del sistema sometida a la resultante de las fuerzas que actúan sobre el mismo. Se utiliza para describir el movimiento de traslación de un sistema de partículas. Vector de posición del centro de masas El vector de posición del centro de masas se define como: Donde M es la masa total del sistema de partículas. La posición del centro de masas no tiene por qué coincidir con la posición de ninguna de las partículas del sistema, es simplemente un punto en el espacio. Velocidad del centro de masas La velocidad del centro de masas es la derivada de su vector de posición: El segundo miembro de la ecuación anterior es el momento lineal total del sistema de partículas dividido por la masa total del sistema, por lo que este último puede obtenerse a partir de la velocidad del centro de masas: Este último resultado significa que el momento lineal total de un sistema de partículas es igual al momento lineal que tendría la masa total del sistema situada en el CM, por lo que el movimiento de traslación del sistema de partículas está representado por el de su centro de masas. Si el sistema de partículas está aislado, su momento lineal será constante, por lo que la velocidad de su centro de masas también lo será. Si colocamos un sistema de referencia en el centro de masas de un sistema de partículas aislado, dicho sistema de referencia (llamado sistema-C) es inercial. Resulta particularmente útil para estudiar las colisiones. Aceleración del centro de masas Cuando un sistema de partículas no está aislado, sobre él actuarán fuerzas internas y externas, representadas respectivamente en la siguiente figura (a) en rojo y en verde; por tanto las partículas de dicho sistema tendrán en general aceleración, y el centro de masas también estará acelerado. Sistema constituído por dos partículas. Sobre él actúan fuerzas internas y externas. En la parte (b) de la figura, se observan las fuerzas externas aplicadas en el centro de masas. Para calcular la aceleración del centro de masas del sistema, vamos a aplicar lasegunda ley de Newton a cada una de las partículas del sistema: Masa 1: Masa 2: Sumando ambas, En el primer miembro aparece la derivada del momento lineal total del sistema (igual al momento de su centro de masas), y en el segundo miembro la suma de las fuerzas internas se anula puesto que cumplen la tercera ley de Newton. La expresión anterior queda entonces: Para un sistema constituido por N partículas, el segundo miembro es la suma de las fuerzas externas que actúan sobre el sistema y por tanto: Que no es más que la segunda ley de Newton para el centro de masas de un sistema de partículas. En la parte (b) de la figura anterior se observa el centro de masas del sistema con las fuerzas externas aplicadas en él.