teorema del valor medio de Cauchy es una generalización delteorema del valor medio (de Lagrange). A partir del mismo puede demostrarse la regla de L'Hôpital, fuerte ayuda para el cálculo de límites con indeterminaciones
 ó
ó  .
.
El teorema se enuncia de la siguiente manera:
|
Nótese el caso particular en el cual g(x)=x, donde entonces la expresión se reduce al teorema del valor medio de Lagrange.
- Sea G(x) una función definida como:
- donde f(x) y g(x) son funciones continuas en [a,b], derivables en (a,b). Se puede observar por simple inspección que G(a)=0 y G(b)=0.
- Por el Teorema de Rolle, existe un c, perteneciente al intervalo (a,b), tal que G'(c)=0. Así, derivando G(x) se obtiene:
- y sabiendo que G'(c) es 0
- de donde se deduce que
- Si g(b)-g(a) y g'(c) son distintos de 0, la expresión anterior puede ser escrita como:
El teorema de Cauchy es usado para la demostración de otros teoremas. Nos permite, entre otros, demostrar la regla de L'Hôpital:
El teorema integral de Cauchy, descubierto por Augustin Louis Cauchy en 1825, es parte fundamental del cálculo integral de variable compleja.
Si f(z) es analítica en un dominio simplemente conexo D y su derivada es continua en D entonces para cualquier contorno cerrado simple contenido en D se tiene:

- Posteriormente, Edouard Goursat demostró que no era necesario considerar la hipótesis de que la derivada de f fuera continua para asegurar que el valor de la integral sea cero. De esta manera:
- El teorema sigue siendo válido cuando el contorno C no es simplemente conexo pero tiene un número finito de "agujeros".
- Sea C un contorno simple cerrado, y sean Cj (j=1, 2, ..., n) un número finito de contornos simples cerrados dentro de C, tales que las regiones interiores a cada Cj no tengan puntos en común. Sea R la región cerrada formada por todos los puntos dentro de C, salvo los puntos interiores a cada Cj. Denotamos por F toda la frontera orientada de R formada por C y todos los contornos Cj, recorridos en un sentido tal que los puntos interiores de R queden a la izquierda de F. Entonces, si f es analítica en todo R,
A raíz de este trabajo, actualmente el teorema es conocido como teorema integral de Cauchy-Goursat. - A partir del teorema de Cauchy-Goursat, se pueden demostrar proposiciones como la siguiente:Sea ƒ(z) analítica sobre C, siendo C un contorno cerrado simple, y en el interior de C. Si se toma un punto interior "
 " de C, se cumple que:que corresponde a la fórmula integral de Cauchy.
" de C, se cumple que:que corresponde a la fórmula integral de Cauchy. - Teorema de Cauchy-Hadamard, llamado así por los matemáticos franceses Augustin Louis Cauchy y Jacques Hadamard, estableciendo el radio de convergencia de una serie de potencias que aproxima una función en torno de un punto a.Considérese la serie de potencias formal de una variable compleja z de la formadonde
 Entonces el radio de convergencia de ƒ en el punto a estará dado pordonde lim sup denota el límite superior, el límite cuando n tiende a infinito del supremo de una sucesión de valores después de la n-ésima posición. Si la secuencia de valores no está acotada, de manera que lim sup sea ∞, entonces la serie de potencias no convergerá cerca de a, mientras que si el lim sup es 0 entonces el radio de convergencia será ∞, lo cual significa que la serie de potencias converge en todo el plano complejo.
Entonces el radio de convergencia de ƒ en el punto a estará dado pordonde lim sup denota el límite superior, el límite cuando n tiende a infinito del supremo de una sucesión de valores después de la n-ésima posición. Si la secuencia de valores no está acotada, de manera que lim sup sea ∞, entonces la serie de potencias no convergerá cerca de a, mientras que si el lim sup es 0 entonces el radio de convergencia será ∞, lo cual significa que la serie de potencias converge en todo el plano complejo. - Sin pérdida de generalidad asumiremos que
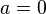 . En primer lugar vamos a demostrar que la serie de potencias
. En primer lugar vamos a demostrar que la serie de potencias  converge para
converge para  , y después que ésta diverge para
, y después que ésta diverge para  .En primer lugar suponemos que
.En primer lugar suponemos que . Sea
. Sea  distinto de cero o infinito. Para todo
distinto de cero o infinito. Para todo  , existe sólo un número finito de
, existe sólo un número finito de  tales que
tales que ![\sqrt[n]{|c_n|}\geq t+\epsilon](https://upload.wikimedia.org/math/2/a/4/2a4f0c7540252ea99cea97db82c3727d.png) . Ahora,
. Ahora, 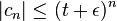 , así que la serie
, así que la serie  converge si
converge si  . Esto demuestra la primera parte.Sea ahora
. Esto demuestra la primera parte.Sea ahora . Tomando
. Tomando 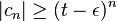 , vemos que la serie no puede converger dado que su n-ésimo término no tiende a 0.
, vemos que la serie no puede converger dado que su n-ésimo término no tiende a 0.
 y
y  continuas en
continuas en ![[a,b]](https://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) y derivables en
y derivables en  . Entonces existe al menos un punto
. Entonces existe al menos un punto  tal que:
tal que:

![G(x) = [g(b)-g(a)] \cdot [f(x)-f(a)] - [f(b)-f(a)] \cdot [g(x)-g(a)] \,\!](https://upload.wikimedia.org/math/a/0/a/a0a51a88646e4c2fa34cedc695a70593.png)
![G'(x) = [g(b)-g(a)]\cdot f'(x)-[f(b)-f(a)] \cdot g'(x)](https://upload.wikimedia.org/math/a/9/3/a9374f31350f459ec3e2d31592bcdbfd.png)
![0 = [g(b)-g(a)] \cdot f'(c)-[f(b)-f(a)]\cdot g'(c)](https://upload.wikimedia.org/math/5/f/9/5f9b83f16d2b827370803d79c1e94610.png)
![[f(b)-f(a)]\cdot g'(c) = [g(b)-g(a)] \cdot f'(c)](https://upload.wikimedia.org/math/6/c/6/6c66e2e171624ed30d5f5c53b77202ef.png)






No hay comentarios:
Publicar un comentario