teorema de Carnot, nombrado así por Lazare Carnot (1753-1823), es el siguiente:
Sea ABC un triángulo cualquiera. Entonces la suma de las distancias desde el circuncentro D a los lados del triángulo ABC es
donde r es el radio del círculo inscrito en el triángulo y R es el radio del círculo circunscrito del triángulo. Aquí, el signo de la distancia es negativa si, y sólo si el segmento DX (X = F, G, H) esta completamente fuera del triángulo. En la imagen de abajo (el caso de un triángulo obtusángulo)DF es negativo y los segmentos DG y DH son positivos.
Un resultado relacionado con el teorema de Carnot es el primer teorema de Mikami-Kobayashi o teorema japonés de polígonos concíclicos.

El teorema de Carnot es un enunciado alternativo del Segundo Principio de la termodinámica, que se formula a partir de la comparación entre máquinas reversibles y máquinas irreversibles como:
El rendimiento de una máquina térmica M que opere entre dos focos no puede ser superior que el de una máquina reversible que opere entre los mismos focos
cumpliéndose la igualdad si la máquina M es también reversible y la desigualdad si es irreversible.
Puede demostrarse que el teorema de Carnot es equivalente al enunciado de Kelvin-Planck, aunque está formulado de una forma mucho más concreta que éste. El de Kelvin-Planck simplemente nos dice que no existe la máquina perfecta con rendimiento del 100%. El teorema de Carnot nos dice además que existe un máximo para ese rendimiento e incluso establece cómo hallar ese máximo. Basta con calcular el rendimiento de una máquina reversible que actúe entre las dos temperaturas indicadas.
Máquinas reversibles puede haber muchas con diferentes soportes (solo gas, agua y vapor, materiales magnéticos,…) por lo que puede resultar sorprendente que el rendimiento de todas ellas sea el mismo si trabajan entre las mismas temperaturas.
Calculando el rendimiento de una en particular, como la de Carnot resulta
siendo Tf la temperatura del foco frío y Tc la del foco caliente, por tanto, el teorema de Carnot equivale a
2 Demostración
Para demostrar la equivalencia del teorema de Carnot con el resto de enunciados nos basta hacerlo con uno de ellos.
Es evidente que si no se cumple el enunciado de Kelvin-Planck no se cumple el teorema de Carnot, ya que una máquina que transformara todo el calor en trabajo tendría un rendimiento de 1, lo que supera el rendimiento de una máquina reversible.
Veamos que el recíproco también es cierto. Supongamos que tenemos dos máquinas térmicas: una máquina térmica M (reversible o irreversible), que tiene un rendimiento ηM y una reversible R, con rendimiento ηR.
Suponemos que el rendimiento de la máquina M es superior al de la máquina R
Esto quiere decir que, para la misma cantidad de calor absorbido | Qc | , la máquina M realiza un trabajo | WM | superior al que hace la máquina R, | WR | y produce menos calor de desecho.
Si ahora invertimos la máquina R, convirtiéndola en un refrigerador, resulta que el conjunto es un dispositivo que no toma calor del foco caliente (ya que el calor | Qc | que toma M lo devuelve R), realiza un trabajo neto | WM | − | WR | y toma una cantidad de calor equivalente del foco frío
esto es, este dispositivo toma calor de un solo foco y lo convierte en trabajo, lo que viola el enunciado de Kelvin-Planck. Concluimos por tanto que debe ser
3 Corolario
En la demostración anterior no se ha supuesto que la máquina M sea irreversible. En el caso particular de que sea reversible (la etiquetamos como R') obtenemos que podemos repetir el razonamiento invirtiendo R' y dejando R como máquina y obtenemos entonces
lo que nos da el corolario al Teorema de Carnot:
Todas las máquinas térmicas reversibles que operen entre las mismas temperaturas poseen el mismo rendimiento
Este rendimiento se puede calcular empleando cualquier máquina de este tipo. La más sencilla es la máquina de Carnot para la cual el rendimiento es
El ciclo de Carnot no es el único que posee esta propiedad. El ciclo de Stirling y el ciclo de Ericsson con recirculación de calor son también ciclos reversibles con el mismo rendimiento.
4 Relación con el aumento de entropía
El teorema de Carnot se relaciona directamente con la producción de entropía en una máquina térmica.
En una máquina que opera cíclicamente:
- La entropía del sistema (la máquina) no cambia en un ciclo, por ser la entropía una función de estado.
- La entropía del ambiente disminuye al ceder calor Qc a una temperatura Tc.
- La entropía del ambiente aumenta al absorber un calor Qf a una temperatura Tf.
La variación total de entropía sería
Esta variación debe ser positiva en una máquina irreversible y nula en una reversible
Por otro lado tenemos que en la misma máquina se cumple el primer principio de la termodinámica
Combinando ambas ecuaciones:
lo que nos dice que el trabajo que puede obtenerse de una máquina es como máximo
y que el rendimiento de una máquina cualquiera es
que para una máquina irreversible será inferior al de una reversible, siendo imposible que sea superior (ya que llo implicaría una disminución de la entropía del universo).
que es de nuevo el enunciado de Kelvin-Planck.
5 Refrigeradores y bombas de calor
La aplicación del teorema de Carnot a un refrigerador establece que el COP máximo lo da un refrigerador que opere según un ciclo reversible, como el de Carnot. Este valor máximo es
Para un frigorífico que mantiene los productos a 5°C en una habitación a 22°C este valor máximo es 16.4. Un frigorífico real posee un COP en torno a 4.
Para una bomba de calor, el COP máximo lo da también una bomba reversible, siendo su valor máximo
Una bomba de calor que mantiene una habitación a 22°C mientras el exterior está a 5°C tiene un coeficiente de desempeño máximo de 17.4 (uno más que para el frigorífico).
teorema de Casey es una generalización del teorema de Ptolomeo, llamado así por el matemático John Casey (1820-1891).
Sea 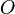 un círculo de radio
un círculo de radio  . Sea
. Sea  (en ese orden) cuatro círculos no interceptados que se encuentran dentro de
(en ese orden) cuatro círculos no interceptados que se encuentran dentro de 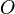 y tangentes a él. Denotemos por
y tangentes a él. Denotemos por  la longitud de la tangente exterior común de los círculos
la longitud de la tangente exterior común de los círculos  . Entonces:
. Entonces:
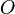 un círculo de radio
un círculo de radio  . Sea
. Sea  (en ese orden) cuatro círculos no interceptados que se encuentran dentro de
(en ese orden) cuatro círculos no interceptados que se encuentran dentro de 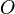 y tangentes a él. Denotemos por
y tangentes a él. Denotemos por  la longitud de la tangente exterior común de los círculos
la longitud de la tangente exterior común de los círculos  . Entonces:
. Entonces:
Nótese que en el caso degenerado, donde los cuatro círculos se reducen a puntoses exactamente el teorema de Ptolomeo.


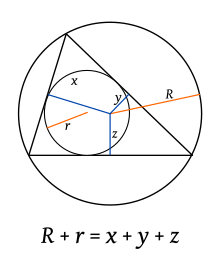



No hay comentarios:
Publicar un comentario