Sea (X,d) un espacio métrico completo y f una aplicación. Se dice que f es contractiva si existe una constante K con 0 para cualesquiera 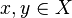 . Un punto fijo
. Un punto fijo  de f es un punto de X tal que
de f es un punto de X tal que  =
=  . Entonces el teorema del punto fijo de Banach dice:
. Entonces el teorema del punto fijo de Banach dice:
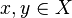 . Un punto fijo
. Un punto fijo  de f es un punto de X tal que
de f es un punto de X tal que  =
=  . Entonces el teorema del punto fijo de Banach dice:
. Entonces el teorema del punto fijo de Banach dice:
|
Además, el teorema establece que para todo punto x de X la sucesión { x, f(x), f(f(x)),...} converge a dicho punto fijo.
Existencia del punto fijo: La demostración se sigue de que la sucesión así definida es una sucesión de Cauchy por ser la función contractiva. Como X es completo, esta sucesión converge a un punto  de X.
de X.
Unicidad del punto fijo: Supongamos que y
y 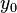 son dos puntos fijos distintos de
son dos puntos fijos distintos de  situados a una distancia
situados a una distancia  uno del otro. Entonces,
uno del otro. Entonces,

y, como es contractiva,
es contractiva,

De lo anterior se sigue que , pero esto es absurdo, por lo que
, pero esto es absurdo, por lo que  no puede tener dos puntos fijos distintos.
no puede tener dos puntos fijos distintos.
 de X.
de X.Unicidad del punto fijo: Supongamos que
 y
y 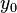 son dos puntos fijos distintos de
son dos puntos fijos distintos de  situados a una distancia
situados a una distancia  uno del otro. Entonces,
uno del otro. Entonces,
y, como
 es contractiva,
es contractiva,
De lo anterior se sigue que
 , pero esto es absurdo, por lo que
, pero esto es absurdo, por lo que  no puede tener dos puntos fijos distintos.
no puede tener dos puntos fijos distintos.
Se trata de una herramienta básica en la demostración de la existencia de soluciones de ecuaciones diferenciales (Véase el teorema de Picard-Lindelöf). Otro de los usos de este resultado radica en el análisis de sistemas dinámicos, que tiene numerosas aplicaciones, por ejemplo en el estudio de modelos de población, modelos caóticos, etcétera. También es importante en el estudio de métodos iterativos utilizados en el cálculo numérico, por ejemplo en algunos problemas de ingeniería. Incluso determinados fractales son puntos fijos de ciertas contracciones.
Teorema de Barbier es aquel que define las características que ha de cumplir una curva para ser de longitud constante.
Según el Teorema de Joseph Emile Barbier, una curva es de longitud constante si su perímetro es igual a la distancia a la que se encuentran las rectas paralelas con respecto a las que su longitud es constante.
La circunferencia
La circunferencia es la curva de longitud constante más evidente: puede ser rotada entre dos segmentos paralelos separados por una distancia constante. La circunferencia cumple el teorema de Barbier, ya que su perímetro (π•d) es igual a la distancia que separa las paralelas multiplicadas por π, es decir π•d).
El Triángulo de Reuleaux
El Triángulo de Reuleaux es un caso de curva de longitud constante no tan evidente como el del círculo. La construcción de este triángulo se hace a partir de un triángulo equilátero ABC, dibujando los arcos BC usando como centro el vértice A, CA con centro en B, y AB con centro en C. Analizando el Teorema de Barbier, el valor del perímetro del Triángulo de Reuleaux es tres veces la longitud de un arco cuyo radio es la distancia entre las paralelas. Dicho arco tiene un ángulo de 60º, es decir, π/3. Por lo tanto, su perímetro es 3•(d•π/3), es decir, π•d, valor que conicide con la distancia entre las paralelas multiplicada por π (π•d).
El teorema de Barbier dice que:
Una curva es de longitud constante si su perímetro es igual a πd, donde d es la distancia a la que se encuentran las rectas paralelas con respecto a las que su longitud es constante.
Por ejemplo, la circunferencia es una curva de longitud constante. Y verifica el teorema de Barbier, ya que su perímetro mide 2πr (r es el radio de la circunferencia) y coincide con la distancia que separa las paralelas (2r) multiplicada por π.
El triángulo de Reuleaux es también una curva de longitud constante. Y, evidentemente, verifica el teorema de Barbier, ya que el perímetro del triángulo de Reuleaux es el triple de la longitud de un arco que determina la distancia d entre las paralelas: su perímetro es 3(dπ/3), es decir, πd.
teorema de Bayes, en la teoría de la probabilidad, es una proposición planteada por el filósofo inglés Thomas Bayes ( 1702-1761)1 en 1763,2 que expresa la probabilidad condicional de un evento aleatorio A dado B en términos de la distribución de probabilidad condicional del evento B dado A y la distribución de probabilidad marginal de sólo A.
En términos más generales y menos matemáticos, el teorema de Bayes es de enorme relevancia puesto que vincula la probabilidad de A dado B con la probabilidad de B dado A. Es decir que sabiendo la probabilidad de tener un dolor de cabeza dado que se tiene gripe, se podría saber (si se tiene algún dato más), la probabilidad de tener gripe si se tiene un dolor de cabeza, muestra este sencillo ejemplo la alta relevancia del teorema en cuestión para la ciencia en todas sus ramas, puesto que tiene vinculación íntima con la comprensión de la probabilidad de aspectos causales dados los efectos observados.
|
Con base en la definición de Probabilidad condicionada, obtenemos la Fórmula de Bayes, también conocida como la Regla de Bayes:
Esta fórmula nos permite calcular la probabilidad condicional  de cualquiera de los eventos
de cualquiera de los eventos 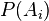 , dado
, dado  . La fórmula
. La fórmula ![[1]](https://upload.wikimedia.org/math/3/5/d/35dba5d75538a9bbe0b4da4422759a0e.png) "ha originado muchas especulaciones filosóficas y controversias".
"ha originado muchas especulaciones filosóficas y controversias".
 de cualquiera de los eventos
de cualquiera de los eventos 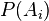 , dado
, dado  . La fórmula
. La fórmula ![[1]](https://upload.wikimedia.org/math/3/5/d/35dba5d75538a9bbe0b4da4422759a0e.png) "ha originado muchas especulaciones filosóficas y controversias".
"ha originado muchas especulaciones filosóficas y controversias".
El teorema de Bayes es válido en todas las aplicaciones de la teoría de la probabilidad. Sin embargo, hay una controversia sobre el tipo de probabilidades que emplea. En esencia, los seguidores de la estadística tradicional sólo admiten probabilidades basadas en experimentos repetibles y que tengan una confirmación empírica mientras que los llamados estadísticos bayesianos permiten probabilidades subjetivas. El teorema puede servir entonces para indicar cómo debemos modificar nuestras probabilidades subjetivas cuando recibimos información adicional de un experimento. La estadística bayesiana está demostrando su utilidad en ciertas estimaciones basadas en el conocimiento subjetivo a priori y el hecho de permitir revisar esas estimaciones en función de la evidencia empírica es lo que está abriendo nuevas formas de hacer conocimiento. Una aplicación de esto son los clasificadores bayesianos que son frecuentemente usados en implementaciones de filtros de correo basura o spam, que se adaptan con el uso. Otra aplicación se encuentra en la fusión de datos, combinando información expresada en términos de densidad de probabilidad proveniente de distintos sensores.
Como observación, se tiene 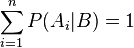 y su demostración resulta trivial.
y su demostración resulta trivial.
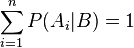 y su demostración resulta trivial.
y su demostración resulta trivial.
Como aplicaciones puntuales:
- El diagnóstico de cáncer.
- Evaluación de probabilidades durante el desarrollo de un juego de bridge por Dan F. Waugh y Frederick V. Waugh.
- Probabilidades a priori y a posteriori.
- Un uso controvertido en La ley de sucesión de Laplace
El teorema de Bayes parte de una situación en la que es posible conocer las probabilidades de que ocurran una serie de sucesos Ai.
A esta se añade un suceso B cuya ocurrencia proporciona cierta información, porque las probabilidades de ocurrencia de B son distintas según el suceso Ai que haya ocurrido.
Conociendo que ha ocurrido el suceso B, la fórmula del teorema de Bayes nos indica como modifica esta información las probabilidades de los sucesos Ai.
Ejemplo: Si seleccionamos una persona al azar, la probabilidad de que sea diabética es 0,03. Obviamente la probabilidad de que no lo sea es 0,97.
Si no disponemos de información adicional nada más podemos decir, pero supongamos que al realizar un análisis de sangre los niveles de glucosa son superiores a 1.000 mg/l, lo que ocurre en el 95% de los diabéticos y sólo en un 2% de las personas sanas.
¿Cuál será ahora la probabilidad de que esa persona sea diabética?
La respuesta que nos dá el teorema de bayes es que esa información adicional hace que la probabilidad sea ahora 0,595.
Vemos así que la información proporcionada por el análisis de sangre hace pasar, la probabilidad inicial de padecer diabetes de 0,03, a 0,595.
Evidentemente si la prueba del análisis de sangre hubiese sido negativa, esta información modificaría las probabilidades en sentido contrario. En este caso la probabilidad de padecer diabetes se reduciría a 0,0016.

A esta se añade un suceso B cuya ocurrencia proporciona cierta información, porque las probabilidades de ocurrencia de B son distintas según el suceso Ai que haya ocurrido.
Conociendo que ha ocurrido el suceso B, la fórmula del teorema de Bayes nos indica como modifica esta información las probabilidades de los sucesos Ai.
Ejemplo: Si seleccionamos una persona al azar, la probabilidad de que sea diabética es 0,03. Obviamente la probabilidad de que no lo sea es 0,97.
Si no disponemos de información adicional nada más podemos decir, pero supongamos que al realizar un análisis de sangre los niveles de glucosa son superiores a 1.000 mg/l, lo que ocurre en el 95% de los diabéticos y sólo en un 2% de las personas sanas.
¿Cuál será ahora la probabilidad de que esa persona sea diabética?
La respuesta que nos dá el teorema de bayes es que esa información adicional hace que la probabilidad sea ahora 0,595.
Vemos así que la información proporcionada por el análisis de sangre hace pasar, la probabilidad inicial de padecer diabetes de 0,03, a 0,595.
Evidentemente si la prueba del análisis de sangre hubiese sido negativa, esta información modificaría las probabilidades en sentido contrario. En este caso la probabilidad de padecer diabetes se reduciría a 0,0016.
Si A 1, A 2 ,... , An son:
Sucesos incompatibles 2 a 2.
Y cuya unión es el espacio muestral (A 1  A 2
A 2  ...
...  A n = E).
A n = E).
Y B es otro suceso.
Resulta que:
Las probabilidades p(A1) se denominan probabilidades a priori.
Las probabilidades p(Ai/B) se denominan probabilidades a posteriori.
Las probabilidades p(B/Ai) se denominan verosimilitudes.

 un conjunto de sucesos mutuamente excluyentes y exhaustivos, y tales que la probabilidad de cada uno de ellos es distinta de cero (0). Sea B un suceso cualquiera del que se conocen las probabilidades condicionales
un conjunto de sucesos mutuamente excluyentes y exhaustivos, y tales que la probabilidad de cada uno de ellos es distinta de cero (0). Sea B un suceso cualquiera del que se conocen las probabilidades condicionales  . Entonces, la probabilidad
. Entonces, la probabilidad 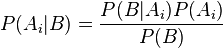
 .
.![P(A_i|B) = \frac{P(B | A_i) P(A_i)}{\sum_{k=1}^n P(B | A_k) P(A_k)}.... [1]](https://upload.wikimedia.org/math/1/4/c/14c61c0d508e0ba073b487b742a19c94.png)
No hay comentarios:
Publicar un comentario