Teoremas epónimos de las matemáticas

Teorema de Cochran

Sean las n variables aleatorias X₁,..., X_n, independientes e idénticamente distribuidas N(0,σ²).

Donde  son formas cuadráticas no negativas definidas en las V.A.  Esto es 

Sea rango  j = 1,...,k

Si 

Entonces:

•  son independientes
• 

TEOREMA DE COCHRAN
si x es un vector aleatorio con distribución:Nn [ M ;V ] , siendo el rango de la matriz de varianzas V : rango ( V)= r
entonces la variable aleatoria obtenida por la forma cuadrática:
(x-M)' V^-1(x-M) seguirá una distribución c2_r
El hecho de restar el vector de medias M y de utilizar como matriz de la forma cuadrática la inversa de la matriz de varianzas V^-1 actua como una especie de "tipificación generalizada que elimina el efecto de la dependencia (correlación)".

teorema de Darboux es un teorema sobre variedades simplécticas que afirma que todas las variedades simplécticas son localmente simplectomórficas. Eso significa, que para toda toda variedad de ese tipo de dimensión 2n existe un homeomorfismo con el espacio lineal simpléctico  dotado de la forma simpléctica canónica ω₀. Equivalentemente el teorema implica que en un entorno de cualquier punto puede definirse un conjunto de coordenadas canónicas.

El teorema fue probado por Jean Gaston Darboux que también probó un resultado análogo en geometría de contacto.

El enunciado preciso del problema es el siguiente:

Sea  una variedad simpléctica de dimensión 2n, donde con  es la 2-forma simpléctica. Entonces para cada punto  existe una carta local  que contiene a P tal que ω tiene la forma:

Enunciado más formalmente

Para cada punto de una variedad simpléctica existe una carta local  tal que si  es el pullback de la forma simpléctica canónica 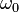 de  entonces:

La carta local U_P se llama carta local de Darboux alrededor de P. La variedad simpléctica  puede ser recubierta mediante unrecubrimiento formado por cartas de Darboux. El conjunto de coordenadas de Darboux se llaman usualmente en mecánica hamiltoniana,coordenadas canónicas.

Este resultado implica que no existen invariantes locales en geometría simpléctica. Siempre se puede escoger un sistema de coordenadas canónicas o coordenadas de Darboux, sea cual sea el punto, es decir, todos los puntos presentan cierta equivalencia. Esto contrata con la situación en geometría riemanniana donde por ejemplo la curvatura es un invariante local que permite distinguir unos puntos de otros. En una variedad riemanniana pueden escogerse siempre coordenadas que hagan que en un punto concreto la métrica sea idéntica a la euclídea, pero en general esto no es posible en todo un entorno del punto. En cambio en una variedad simpléctica las coordenadas que hacen de la forma simpléctica la canónica pueden extenderse a todo un entorno del punto.

Propiedad de Darboux

Si una función es continua en el intervalo [a, b] y k es un número comprendido entre los valores f(a) y f(b), entonces existe algún c en (a, b) tal que f(c) = k

Si Observamos el dibujo podemos definir la propiedad de Darboux de este otro modo:

Si una función es continua en el intervalo [a, b] la función alcanza en este intervalo todos los valores comprendidos entre f(a) y f(b).

Probar que la función f(x) = x(sen x +1) toma el valor 2.

La función es continua en toda  por se el producto de dos funciones continuas.

Tomamos el intervalo  y estudiamos el valor de las imágenes de los extremos:

Por tanto existe un c   tal que f(c) = 2

El teorema de De Gua, llamado así en honor al matemático francés Jean-Paul de Gua de Malves, es un análogo en tres dimensiones del teorema de Pitágoras. Este teorema establece que si un tetraedro posee un vértice formado por ángulos rectos (como en el caso de los vértices de un cubo), entonces el cuadrado del área de la cara opuesta a dicho vértice es igual a la suma de los cuadrados de las áreas de las otras tres caras. A partir de las figuras:

Vista frontal: cara opuesta al vértice.	Vista trasera: caras que forman los ángulos rectos del vértice	Vista lateral

El teorema de Pitágoras y el teorema de De Gua son casos especiales (para un número de dimensiones n = 2 y n = 3 respectivamente) de un teorema general para un símplex que posea un vértice con un ángulo recto.