Caso general
|
Enunciado del teorema en dos variables
|
Demostración
Sea
 .
.
Y sean  ,
,  reales tales que
reales tales que  . Lo cual es posible, ya que
. Lo cual es posible, ya que  es un abierto de
es un abierto de  .
.
 ,
,  reales tales que
reales tales que  . Lo cual es posible, ya que
. Lo cual es posible, ya que  es un abierto de
es un abierto de  .
.
Se definen dos funciones 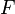 y
y 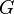
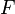 y
y 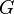
 ,
, ,
,
de modo que:
 .
. ,
,
Aplicando dos veces el teorema de Lagrange:
![F(t) - F(0) = (t - 0) F'(\xi_1) = t \left[ \frac{\partial f}{\partial x} (x_0 + \xi_1, y_0 + s) - \frac{\partial f}{\partial x} (x_0 + \xi_1, y_0) \right] =](https://upload.wikimedia.org/math/4/0/c/40c0284527aa02c862ec9705a34caa7d.png)
 ,
,
y análogamente:
 ,
,
con  ,
,  , por comodidad de escritura pero sin perder generalidad, se suponen
, por comodidad de escritura pero sin perder generalidad, se suponen  .
.
 ,
,  , por comodidad de escritura pero sin perder generalidad, se suponen
, por comodidad de escritura pero sin perder generalidad, se suponen  .
.
Luego haciendo tender 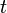 y
y  a
a  se logra la tesis.
se logra la tesis.
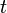 y
y  a
a  se logra la tesis.
se logra la tesis.
3. DERIVADAS PARCIALES
Si y = f(x) es una función de una variable. Su primera derivada
se interpreta como la razón de cambio instantanea de y con respecto de x.
Para una función z = f(x, y) de dos variables, se comprende que de manera analoga la razón con la que cambia al variar x y y (ya sea de manera individual o simultaneamente).
La razón de cambio de z con respecto de x, se obtiene dejando fija a y y calculando la derivada ordinaria de la función z = f(x, y)
Del mismo modo, la derivada parcial de f con respecto de y en el punto (a, b), se obtiene dejando fija a x y calculando la derivada ordinaria de la función z = f(x, y) donde x = a es constante se denota como
Algunas otras notaciones comunes para las derivadas parciales son:
Observemos que si eliminamos la variable y de la ecuación (2), tendriamos el límite de la ecuación (1). Esto significa que podemos calcular (2) como una derivada ordinaria con respecto de x, considerando ay como constante durante el proceso de derivación . De manera similar, podemos calcular (3) como una derivada ordinaria, tomando a y como la única variable y tratando a x como una constante durante el cálculo.
Regla para hallar derivadas parciales de z = f(x, y)
Para hallar Dx, considere y como constante y derive f(x,y) con respecto ax
Para hallar Dy, considere x como constante y derive f(x,y) con respecto ay
|
Ejemplo 1. Si 
Solución Conservando y constante y derivando con respecto a x, obtenemos
Conservando a x constante y derivando con respecto a y, obtenemos
Ejemplo 2. Si 
Solución tenemos que la derivada de la función es de la forma d( f ) =d( U V )
Ejemplo 3. Si  evalue la pendiente en dirección de x en el punto (0,2)
evalue la pendiente en dirección de x en el punto (0,2)
Solución tenemos que la derivada de la función es de la forma d( f ) =d( U / V )
DERIVADAS PARCIALES DE SEGUNDO ORDEN
Cuando diferenciamos dos veces una función, producimos sus derivadas de segundo orden. Estas derivadas son usualmente denotadas por
Teorema de Euler, Teorema de Clairaut (Teorema de las derivadas cruzadas)
Si f(x,y) y sus derivadas parciales fxy, fyx están definidas en un disco D que contiene al punto (a,b) y son todas continuas en (a,b), entonces
fxy (a,b) = fyx (a,b)
|
Las derivadas parciales de orden mayor de 2 o de orden superior también se puden definir. Por ejemplo
y usando el Teorema de Euler o Clairaut se demuestra que fxyy = fyxy = fyyx si estas funciones son continuas.
Ejemplo 4. Calcule fyyzx si 
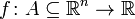 , A un conjunto abierto, tal que existen las segundas derivadas cruzadas y son continuas en A.
, A un conjunto abierto, tal que existen las segundas derivadas cruzadas y son continuas en A. se cumple que:
se cumple que:

 del plano
del plano  . Si existen las segundas derivadas cruzadas y son continuas en
. Si existen las segundas derivadas cruzadas y son continuas en  ) estas son iguales, es decir:
) estas son iguales, es decir: .
.
No hay comentarios:
Publicar un comentario