Teorema de Gauss-Márkov, formulado por Carl Friedrich Gauss y Andréi Márkov, establece que en un modelo linealgeneral (MLG) en el que se establezcan los siguientes supuestos:
- Correcta especificación: el MLG ha de ser una combinación lineal de los parámetros (
 ) y no necesariamente de las variables:
) y no necesariamente de las variables: 
- Muestreo aleatorio simple: la muestra de observaciones del vector
 es una muestra aleatoria simple y, por lo tanto, el vector
es una muestra aleatoria simple y, por lo tanto, el vector  es independiente del vector
es independiente del vector 
- Esperanza condicionada de las perturbaciones nula:

- Correcta identificación: la matriz de regresoras (X) ha de tener rango completo: rg(X)=K<=N
- Homocedasticidad:

el estimador mínimo cuadrático ordinario (MCO) de B es el estimador lineal e insesgado óptimo (ELIO o BLUE: best linear unbiased estimator), es decir, el estimador MCO es el estimador eficiente dentro de la clase de estimadores lineales e insesgados.
Dicho teorema se basa en 10 supuestos, denominados, Supuestos de Gauss Márkov; que sirven como hipótesis a la demostración del mismo:
- El modelo esta correctamente especificado.
- Debe ser lineal en los parámetros.
- El valor de la media condicional es cero.
- Hay homocedasticidad.
- No existe correlación entre las perturbaciones.
- La covarianza entre
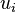 y
y 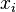 es cero.
es cero. - El número de observaciones es mayor que el de parámetros.
- Existe variabilidad entre los
 .
. - No hay multicolinealidad perfecta.
- Las
 son no estocásticas, es decir, son fijas en muestras repetidas.
son no estocásticas, es decir, son fijas en muestras repetidas.
teorema de Gelfond-Schneider es un resultado que establece la trascendencia de una gran clase de números. Fue probado originalmente por Alexander Gelfond en 1934 y de nuevo de forma independiente por Theodor Schneider, en 1935. El teorema Gelfond–Schneider es una respuesta parcial al séptimo problema de Hilbert.Si  y
y  son números algebraicos en el cuerpo de los números complejos (siendo
son números algebraicos en el cuerpo de los números complejos (siendo  ), y si
), y si  no es un número racional, entonces cualquier valor de αβ es un número trascendente.
no es un número racional, entonces cualquier valor de αβ es un número trascendente.
 y
y  son números algebraicos en el cuerpo de los números complejos (siendo
son números algebraicos en el cuerpo de los números complejos (siendo  ), y si
), y si  no es un número racional, entonces cualquier valor de αβ es un número trascendente.
no es un número racional, entonces cualquier valor de αβ es un número trascendente.- En general,
 es multivaluada, donde "log" es el logaritmo complejo. Ésta es la razón de la expresión "cualquier valor de" en el enunciado.
es multivaluada, donde "log" es el logaritmo complejo. Ésta es la razón de la expresión "cualquier valor de" en el enunciado. - La siguiente es una formulación equivalente del teorema: si
 y
y  son números algebraicos diferentes de cero, y
son números algebraicos diferentes de cero, y  , entonces
, entonces  es (real) racional o trascendente.
es (real) racional o trascendente. - Si se elimina la restricción de que
 sea algebraica, el enunciado no será cierto en el caso general (escójanse
sea algebraica, el enunciado no será cierto en el caso general (escójanse  y
y  , que es trascendente, y
, que es trascendente, y  , que es algebraico). No se conoce una caracterización de los valores de α y β que produzca un αβ trascendente.
, que es algebraico). No se conoce una caracterización de los valores de α y β que produzca un αβ trascendente.
Se deriva inmediatamente del teorema la trascendencia de los siguientes números:
- Los números
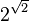 (la constante de Gelfond-Schneider) y
(la constante de Gelfond-Schneider) y  (véase demostración no constructiva).
(véase demostración no constructiva). - El número
 (constante de Gelfond), dado que
(constante de Gelfond), dado que  es uno de los valores de
es uno de los valores de  .
.
teorema de Gerschgorin es utilizado en álgebra lineal para encontrar una cota de los autovalores de una matriz compleja (esto incluye también a las reales) de orden nxn. Fue publicado por el matemático soviético S.Gerschgorin en 1931. 1
Dada una matriz  se definen los círculos
se definen los círculos  con centro en
con centro en 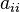 y radio
y radio  . El teorema afirma que los autovalores de la matriz A se encuentran en la unión de los n círculos. Además, cada componente conexa de esa unión contiene tantos autovalores como círculos haya en ella, donde círculos y autovalores son contados con multiplicidad.
. El teorema afirma que los autovalores de la matriz A se encuentran en la unión de los n círculos. Además, cada componente conexa de esa unión contiene tantos autovalores como círculos haya en ella, donde círculos y autovalores son contados con multiplicidad.
 se definen los círculos
se definen los círculos  con centro en
con centro en 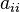 y radio
y radio  . El teorema afirma que los autovalores de la matriz A se encuentran en la unión de los n círculos. Además, cada componente conexa de esa unión contiene tantos autovalores como círculos haya en ella, donde círculos y autovalores son contados con multiplicidad.
. El teorema afirma que los autovalores de la matriz A se encuentran en la unión de los n círculos. Además, cada componente conexa de esa unión contiene tantos autovalores como círculos haya en ella, donde círculos y autovalores son contados con multiplicidad.Teorema de Gerschgorin, condición mecánica y forma final de la relación de dispersión.
Ahora analizamos una forma, para encontrar el rango de eigenvalores de una matriz y una condición mecánica para el modelo empleado. Supongamos que
nos interesa una componente, que explícitamente será:
Pasando al lado derecho el término
Como siempre existe por lo menos un eigenvector distinto de cero supongamos que es el
Supongamos además, que la componente
Como
Este resultado es conocido como ``teorema de Gerschgorin'' (Ref. [12]) que nos dice: Que en el plano complejo cada eigenvalor de la matriz de elementos complejos
Como no sabemos cual de las componentes es la máxima, entonces se construyen los discos para cada una de las componentes y si no es el disco que interesa, no lo tomamos en cuenta, pero si lo es, entonces va a incluir el eigenvalor en cuestión; aunque es posible que al cambiar el eigenvalor cambie el elemento donde se alcanza el máximo, pero no importa, ya que se tienen todos los discos y en algunos de ellos se encuentra el eigenvalor.
Por lo tanto lo anterior nos da una información de los eigenvalores en particular, en el caso que estamos tratando, nos dice que se tienen un círculo con centro
Ahora en el caso de vibraciones mecánicas, se tiene la siguiente restricción
Como vemos en este diagrama de fuerzas, si movemos una partícula desde su posición de equilibrio, el efecto de la interacción en ambos lados debe ser el mismo debido a la simetría de la cadena, por lo tanto va a interaccionar con las partículas en ambos lados y es precisamente la constante del resorte la que influye en el equilibrio de fuerzas.
La restricción es gráficamente razonable de postular, únicamente para nuestro caso que es un sistema vibracional, ya que en otros sistemas no es válida, como por ejemplo en problemas de mecánica cuántica, esto es sistema de electrones
Además si no fuera físicamente razonable postular que
Tenemos la restricción en la forma:
y del teorema de Gershgorin dado por la relación
| (4.4) |
lo cual nos permite escribir esto como
Sustituyendo el valor de
Analizando este resultado, vemos una justificación más de que las frecuencias resultan imaginarias, con la posibilidad de que sean cero, pero nunca tendremos el caso
Por lo tanto de (4.5) y (4.2) resulta:
Al menos en el rango en que
Ahora lo que nos interesa es calcular los eigenvalores de la matriz
también vimos que las raíces ocurren en parejas recíprocas, supongamos que son:  por lo tanto podemos definir el siguiente arreglo:
por lo tanto podemos definir el siguiente arreglo:
y debido precisamente a la forma de la ecuación característica, o lo que es lo mismo de la matriz de transferencia, es posible escribir el polinomio característico como
factorizando y reagrupando términos resulta finalmente que
| (4.8) | |||
| (4.9) |
Resolviendo este sistema de ecuaciones resulta:
| (4.10) |
Además estamos interesados en regiones en que ``
La condición para que sea real puro es que el descriminante de la ecuación sea cero, esto es:
y utilizando la condición mecánica, esto es
resulta finalmente:
Que es exactamente la misma relación que se obtiene al considerar únicamente la condición mecánica, después de ciertos artificios matemáticos.
Otro resultado importante que se puede deducir de las ecuaciones anteriores, es la relación entre las constantes de interacción a primeros y segundos vecinos, esto lo podemos ver de la siguiente manera.
Usando el resultado de que
factorizando y agrupando términos resulta
Analizando esta última desigualdad vemos que
lo cual quiere decir que  en cuyo caso, hay raíces complejas y por lo tanto habrá factores de fase compleja; para
en cuyo caso, hay raíces complejas y por lo tanto habrá factores de fase compleja; para  existirán amortiguaciones puras, o soluciones puramente oscilatorias, en el valor extremo de
existirán amortiguaciones puras, o soluciones puramente oscilatorias, en el valor extremo de  ; el caso en que
; el caso en que  es una razón crítica.
es una razón crítica.
Anteriormente mencionamos como una relación de dispersión puede ser deducida, a partir de la ecuación característica, la obtención es directa como podemos apreciarlo de la siguiente forma: Usando la ecuación (4.6), junto con los parámetros definidos en (2.13) resulta:
despejando  resulta:
resulta:
| (4.12) |
Que es la relación de dispersión, ya que nos da una relación de frecuencia espacial, con la temporal.
La gráfica de esta relación de dispersión es la siguiente:Otra relación de dispersión que nos puede dar bastante información se obtiene de la siguiente forma.
Pongamos los elementos de la matriz de transferencia
Para solucionar este sistema de ecuaciones, despejamos
Por lo tanto las soluciones para ``
Esta ecuación es una relación de dispersión porque relaciona a ``
Es conveniente poner la ecuación (4.15) en una forma más explícita anteriormente definimos
por lo tanto
Por lo tanto la ecuación (4.15) queda finalmente como:
Que es la relación de dispersión para el interior de cualquier cadena por lo tanto es conveniente analizarla en forma detallada.
Lo que interesa en principio es analizar cuándo la expresión es real o compleja, ya que si
Por lo tanto la frontera entre real y complejo es cuando el discriminante de (4.16) es igual a cero, esto es
despejando  resulta
resulta
| (4.17) |
Esta ecuación la podemos graficar, ya que
Cuando
Para obtener un extremo calculemos la derivada, esto es
Como nos interesa un extremo, hagamos  , entonces
, entonces
Por lo tanto en  . Evaluando
. Evaluando  en los puntos
en los puntos  resulta
resulta
Y es fácil comprobar que ocurre un mínimo en
Además, cuando
Con todos estos datos podemos construir la gráfica de la frontera entre la parte real y compleja
Como se puede ver, por combinaciones de
Analicemos las diferentes regiones correspondientes a los distintos valores que puede tomar el parámetro
Caso Real.
Caso Imaginario
Caso en que existe un cambio de fase.
Ahora estamos interesados en contornos en los que
Despejando  resulta
resulta
Que es finalmente la relación de dispersión para el interior de cualquier cadena, que nos interesa graficar e interpretar físicamente, además graficaremos
Analizando la ecuación (4.19), vemos que es necesario tomar valores seleccionados de
Si
Si
| (4.20) |
Debido a que
Si
Si  entonces
entonces 
En  resulta que
resulta que  que es un polo.
que es un polo.
Por lo tanto con estos elementos podemos graficar la ecuación (4.19) esto es:
Prosiguiendo el análisis de la ecuación (4.18). Si
Cuando
En
En
lo cual quiere decir que hay siempre dos valores de  para cualquier
para cualquier  que esté en el intervalo
que esté en el intervalo  , tal que
, tal que  está en el intervalo
está en el intervalo  . En otra región, por supuesto que también dos valores reales para
. En otra región, por supuesto que también dos valores reales para  , pero necesariamente ambas estarán situadas en el intervalo (esto es
, pero necesariamente ambas estarán situadas en el intervalo (esto es  ).
).
Por lo tanto, como las gráficas (IV.II) y (IV.III) pertenecen a la misma ecuación, deducidas únicamente con análisis diferentes, entonces podemos superponerlas y formar una sola, juntamente con los resultados del análisis de dicha ecuación (4.18), esto esAnalizando esta gráfica, junto con las ecuaciones (4.18) y (2.20) resultan las siguientes regiones características:
- Región I.
- Se encuentra en
, esta es una región en donde el número de onda (
) es un número complejo con parte real cero, en este caso el movimiento de la cadena es ondulatorio, ya que resulta una función senosoidal o cosenoidal.
- Región II.
- Está limitada por dos curvas asintóticas, descritas anteriormente (gráfica IV.II) correspondiente a la ecuación
. Es una región de
complejo, por lo tanto tenemos una onda modulada por un factor exponencial que depende de la parte real de
, este factor no es otra cosa que la amplitud, que nos va a modular las funciones seno o coseno.
- Región III.
- Esta región corresponde a valores de
, en esta región el número de onda es real positivo o negativo, por lo tanto el movimiento de las partículas en la cadena estará descrito por una exponencial creciente o decreciente dependiendo de que
ó
.
- Región IV.
- Se encuentra localizada en donde
toma valores reales negativos (en la gráfica corresponde a
) este caso se cumple cuando
dando como resultado que
por lo tanto en este caso se observarán oscilaciones con inversiones de fase, producidas por un desfasamiento de
, este caso tiene que ver con el hecho de que exista cooperación o antagonismo entre primeros y segundos vecinos.
No hay comentarios:
Publicar un comentario