Teoremas epónimos de las matemáticas

teorema de Fubini, llamado así en honor del matemático italiano Guido Fubini, afirma que si:

la integral respecto al producto cartesiano de dos intervalos en el espacio

puede ser escrita como:

Las primeras dos integrales son simples, mientras que la tercera es una integral en el producto de dos intervalos.

Por otra parte si:

entonces:

Por lo tanto la integral doble es reducible al producto de dos integrales simples.

Una aplicación del teorema de Fubini es la evaluación de la "integral de Gauss" (también llamada "integral gaussiana" o "integral de probabilidad"), la cual es base de una gran parte de la teoría de probabilidad:

Para ver como es usado el "teorma de Fubini" para probar éste importante resultado, véase la integral de Gauss.

Cuando tenemos una función continua de varias variables, - llamémosla f(x,y)- podemos realizar su integral en una región del plano - llamémosla R - en lugar de en un intervalo [a,b] con el que estamos acostumbrados a trabajar.

Escribiremos entonces , ∫Rf(x,y) dA donde R es la región de integración y dA es un "diferencial de área".

En este tipo de integrales, se cumplen las siguientes propiedades:

∫RK⋅f(x,y) dA=K⋅∫Rf(x,y) dA

donde K es una constante.

∫Rf(x,y)±g(x,y) dA=∫Rf(x,y) dA±∫Rg(x,y) dA

Si R=R1∪R2, es decir si R es la unión disjunta de R1 y R2

∫Rf(x,y) dA=∫R1f(x,y) dA+∫R2f(x,y) dA

En el caso de que estemos integrando en un rectángulo del plano [a,b]×[c,d], podemos escribir la integral:

∫dc∫baf(x,y) dxdy

Hay que tener en cuenta que en este caso, [a,b] es el intervalo de integración en el eje de las x, mientras que [c,d] es el intervalo de integración en el eje de las y.

En este caso escribiremos

∫dc(∫baf(x,y) dx)dy=∫ba(∫dcf(x,y) dy)dx

Esta propiedad se llama el teorema de Fubini.

Para calcular estas integrales, realizaremos primero la integral de dentro, tomando la otra variable como una constante, y luego, con la primera variable eliminada, integramos respecto a la segunda.

Ejemplo

∫10∫π20eysinx dxdy=∫10ey∫π20sinx dxdy∫ey[−cosx]π20 dy=

∫10ey dy=[ey]10e−1

teorema de Fuchs, expresa la propiedad de ciertas ecuaciones diferenciales de segundo orden, en cuanto a poseer una solución expresada mediante una serie de potencias.

En las matemáticas, el teorema de Fuch, establece la existencia de soluciones de una ecuación diferencial de segundo orden del tipo:

donde ,  y  poseen expansión en series de potencias en .

En este caso existe entonces una solución a esta ecuación diferencial de segundo orden que puede ser expresada mediante una serie de potencias en . Por lo tanto toda solución se puede escribir como

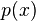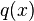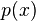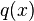para algún  real, donde su radio de convergencia es por lo menos mayor que el menor radio de convergencia de ,  y .

 teorema fundamental de la teoría de Galois es un resultado que describe la estructura de ciertos tipos deextensiones de cuerpos.

En su forma más básica el teorema dice que dada una extensión de cuerpos E/F que sea finita y Galois, existe una correspondencia uno a uno entre sus cuerpos intermedios (cuerpos K que satisfacen F  K  E; también llamados subextensiones de E/F) y los subgruposde su grupo de Galois.

Para extensiones finitas, la correspondencia puede describirse explícitamente como sigue:

• Para cada subgrupo H de Gal(E/F), el cuerpo correspondiente, denotado normalmente E^H, es el conjunto de aquellos elementos de Eque son fijos para cada automorfismo en H.
• Para cada cuerpo intermedio K de E/F, el subgrupo correspondiente es precisamente Aut(E/K), esto es, el conjunto de aquellos automorfismos en Gal(E/F) que dejan fijo a cada elemento de K.

Por ejemplo, el cuerpo más "grande" E se corresponde al subgrupo trivial de Gal(E/F), y el cuerpo base F se corresponde al grupo completo: Gal(E/F).

La correspondencia tiene las siguientes propiedades útiles:

• Es revertible por inclusión. La inclusión de subgrupos H₁  H₂ se da si y sólo si se da también la inclusión en cuerpos: E^H₁  E^H₂.
• Los grados de las extensiones están relacionados con el orden de los grupos de manera consistente con la propiedad anterior. Concretamente, si H es un subgrupo de Gal(E/F), entonces |H| = [E:E^H] y [Gal(E/F):H] = [E^H:F].
• El cuerpo E^H es una extensión normal de F si y sólo si H es un subgrupo normal de Gal(E/F). En este caso, la restricción de los elementos de Gal(E/F) al E^H induce un isomorfismo entre Gal(E^H/F) y el grupo cociente Gal(E/F)/H.

El teorema transforma el problema de clasificar los cuerpos intermedios de E/F en el problema menos difícil de listar los subgrupos de cierto grupo finito.

Por ejemplo, para demostrar que la ecuación general de quinto grado no es resoluble por radicales (ver teorema de Abel-Ruffini), se debe establecer el problema en términos de extensiones radicales (extensiones de la forma F(α) donde α es una n-sima raíz de algún elemento de F), y entonces usar el teorema fundamental para convertir esta afirmación en un problema sobre grupos que ya podamos atacar más directamente.

Las teorías como Teoría de Kummer y la teoría de cuerpos de clases se derivan del teorema fundamental.