Teorema de Carathéodory
En la rama del análisis matemático una parte relevante es la denominada teoría de la medida, la cual estudia la medida de conjuntos y les asigna un valor a éstos. En la vida cotidiana medimos o clasificamos los conjuntos según su longitud, superficie o volumen, incluso utilizamos otras magnitudes como la densidad, peso, viscosidad, dureza y muchas otras características que puedan ocurrírsenos. En matemáticas los conjuntos se pueden separar en aquellos que pueden medirse y aquellos que no; intuitivamente podemos pensar que esto es absurdo, puesto que todo conjunto tiene una de estas medidas mencionadas recientemente, pero lo cierto es que existen numerosos más conjuntos no medibles que medibles, que a priori no encontramos en la naturaleza, y estos no medibles son incluso difícil de definir explícitamente en muchos casos.
Puesto que una medida es una aplicación como veremos más adelante, pueden existir varias medidas; una destacable es la medida de Lebesgue en la que se asientan las bases de la integral de Lebesgue.
Para comprender el teorema de Carathéodory es aconsejable recordar el concepto o definición de medida.
(i)
(ii)Dados
sucesión de M i
,
Si
es una medida en X, decimos que
es un espacio de medida.
Definición: (Medida exterior) Una medida exterior en X es una aplicación ![\mu^{\ast}: \wp(X)\longrightarrow[0,+\infty]](https://upload.wikimedia.org/math/7/5/1/751e261732cffc3908d5c039777f6ded.png) que cumple tres propiedades:
que cumple tres propiedades:
![\mu^{\ast}: \wp(X)\longrightarrow[0,+\infty]](https://upload.wikimedia.org/math/7/5/1/751e261732cffc3908d5c039777f6ded.png) que cumple tres propiedades:
que cumple tres propiedades:(i)
(ii) Si(iii)
-subaditividad Si
sucesión de
entonces

Propiedad: Toda medida en X, definida en  , es una medida exterior en X. (El recíproco no es cierto).
, es una medida exterior en X. (El recíproco no es cierto).
 , es una medida exterior en X. (El recíproco no es cierto).
, es una medida exterior en X. (El recíproco no es cierto).
Es por ese motivo que las medidas exteriores son más fáciles de construir que las medidas. Para construir la medida de Lebesgue lo que se hace es, construir una medida exterior, denominada medida exterior de Lebesgue, ya que es más fácil de construir y utilizando el teorema de Carathéodory podemos definir la medida de Lebesgue con la que se asientan lan bases de la integral de Lebesgue.
Sea  una medida exterior en X. Entonces el conjunto
una medida exterior en X. Entonces el conjunto  formado por todos los conjuntos
formado por todos los conjuntos  -medibles es una
-medibles es una  -álgebra en X y
-álgebra en X y  (
( restringida en
restringida en  ) es una medida en X. Además,
) es una medida en X. Además, 
 una medida exterior en X. Entonces el conjunto
una medida exterior en X. Entonces el conjunto  formado por todos los conjuntos
formado por todos los conjuntos  -medibles es una
-medibles es una  -álgebra en X y
-álgebra en X y  (
( restringida en
restringida en  ) es una medida en X. Además,
) es una medida en X. Además, 
En particular,  es una medida completa, es decir, si
es una medida completa, es decir, si  y
y  entonces todo
entonces todo 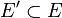 también cumple
también cumple  y
y  .
.
 es una medida completa, es decir, si
es una medida completa, es decir, si  y
y  entonces todo
entonces todo 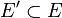 también cumple
también cumple  y
y  .
.
Es relevante destacar que el teorema muestra también como construir la medida exterior a partir de una medida cualquiera definida en una semi-álgebra (como por ejemplo, los intervalos semiabiertos en  ). Así, si la medida definida en la semiálgebra es
). Así, si la medida definida en la semiálgebra es  , la medida exterior estará dada por
, la medida exterior estará dada por  , donde
, donde 
 ). Así, si la medida definida en la semiálgebra es
). Así, si la medida definida en la semiálgebra es  , la medida exterior estará dada por
, la medida exterior estará dada por  , donde
, donde 
En el caso particular de  , la semiálgebra es
, la semiálgebra es ![S=\{(a,b]: a,b \in \mathbb{R} \}](https://upload.wikimedia.org/math/2/f/5/2f5e6b7ea0695fabc04e65b31afe9aab.png) , y la medida sobre ella está dada por
, y la medida sobre ella está dada por ![\nu((a,b]) = b-a](https://upload.wikimedia.org/math/2/e/2/2e233b4765c7e6b6ee22d3acf362ef83.png) .
.
 , la semiálgebra es
, la semiálgebra es ![S=\{(a,b]: a,b \in \mathbb{R} \}](https://upload.wikimedia.org/math/2/f/5/2f5e6b7ea0695fabc04e65b31afe9aab.png) , y la medida sobre ella está dada por
, y la medida sobre ella está dada por ![\nu((a,b]) = b-a](https://upload.wikimedia.org/math/2/e/2/2e233b4765c7e6b6ee22d3acf362ef83.png) .
.
Teorema (Carathéodory coloreado, Bárány 1982).
Dados  conjuntos
conjuntos  en
en  y un punto
y un punto  tal que
tal que  para cada
para cada  , existen puntos
, existen puntos  de tal forma que
de tal forma que  .
.
Por ejemplo, en el plano, si hay 3 triángulos monocromáticos que contienen un punto, hay un triángulo heterocromático que también lo atrapa.
Una pregunta natural es: si se puede garantizar que hay un simplejo heterocromático que atrapa al punto, ¿cuál es la mínima cantidad  de simplejos con esa propiedad que puedo garantizar? Para esto vamos a suponer que cada conjunto contiene
de simplejos con esa propiedad que puedo garantizar? Para esto vamos a suponer que cada conjunto contiene  puntos y
puntos y  está en el interior de las envolventes convexas (si no, considerando
está en el interior de las envolventes convexas (si no, considerando  copias de
copias de  , solo obtenemos un simplejo atrapando al punto, por lo que sin suponer algún tipo de posición general el problema no es interesante).
, solo obtenemos un simplejo atrapando al punto, por lo que sin suponer algún tipo de posición general el problema no es interesante).
El teorema que mencioné muestra que  , y la mejor cota superior que se conocía es
, y la mejor cota superior que se conocía es  , por una construcción de Deza et al. [1], quienes conjeturaban que esta cota era óptima. Hace poco acaba de salir un manuscrito de Pauline Sarrabezolles, dando una respuesta afirmativa a la conjetura. Es decir,
, por una construcción de Deza et al. [1], quienes conjeturaban que esta cota era óptima. Hace poco acaba de salir un manuscrito de Pauline Sarrabezolles, dando una respuesta afirmativa a la conjetura. Es decir,  .
.
La idea de la demostración se basa en una reducción del problema geométrico a uno combinatorio, estudiando lo que se llaman “configuraciones octaedrales”. La idea de la reducción nace a partir de las siguientes dos observaciones
- Una versión fuerte del teorema de Carathéodory coloreado demuestra que solo es esencial que
de los colores contengan al origen [2]. Entonces, para cada vértice de la configuración de puntos, hay un simplejo heterocromático que usa ese vértice y contiene a
. Esto demuestra automáticamente que
, pero queremos más.
- Si consideramos
puntos de cada color, podemos representarlos como los vértices de un octaedro en
. Como los simplejos heterocromáticos representan la imagen de las caras de dicho octaedro (el cual es isomorfo a una esfera), cada punto en
está cubierto una cantidad par de veces por dichos simplejos.
Entonces uno puede definir una hipergráfica a partir del problema con un vértices por cada punto considerado en  y una hiperarista (de tamaño
y una hiperarista (de tamaño  ) por cada simplejo heterocromático que atrapa al punto que queremos. Entonces, tenemos una hipergráfica con
) por cada simplejo heterocromático que atrapa al punto que queremos. Entonces, tenemos una hipergráfica con  clases de vértices de tamaño al menos
clases de vértices de tamaño al menos  cada uno de tal forma que
cada uno de tal forma que
- Cada vértice está en al menos una arista
- Si consideramos dos vértices de cada clase, la hipergráfica inducida por ellos tiene una cantidad par de vértices.
La idea es probar que cada hipergráfica de este tipo tiene al menos  aristas. Esto es lo que demuestra Sararabezolles, olvidándose de la primer condición y usando inducción sobre el mínimo número de aristas garantizadas si dicha condición sucede sólo para los vértices de
aristas. Esto es lo que demuestra Sararabezolles, olvidándose de la primer condición y usando inducción sobre el mínimo número de aristas garantizadas si dicha condición sucede sólo para los vértices de  de las clases.
de las clases.
El teorema de Carathéodory-Jacobi-Lie es un teorema en la topología simpléctica que generaliza el teorema de Darboux.
El enunciado es el el que sigue. Sea M una variedad simpléctica de dimensión 2n con forma simpléctica ω. Sean
funciones diferenciables en un entorno abierto V de a cuyas diferenciales son linealmente independientes en cada punto, o equivalentemente
donde
- {fi, fj} = 0.
(En otras palabras, están en involución dos a dos.) Aquí {-,-} es el paréntesis de Poisson. Entonces existen funciones
definidas en un entorno abierto 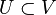 de a tales que
de a tales que
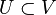 de a tales que
de a tales que- (fi, gi)
es una carta simpléctica de M, es decir, ω se expresa en U como
 .
.- teorema de Carmichael, nombrado así en honor al matemático estadounidense R.D. Carmichael, establece que para todo n mayor que 12, el n-ésimo número de Fibonacci F(n) tiene al menos un factor primo que no es factor de ninguno de los términos anteriores de la sucesión. Las únicas excepciones para n menor o igual que 12 son:
- F(1)=1 y F(2)=1, que no tienen factores primos
- F(6)=8, cuyo único factor primo es 2 (que es F(3))
- F(12)=144, cuyos únicos factores primos son 2 (que es F(3)) y 3 (que es F(4))
Si un número primo p es un factor de F(n) y no es factor de ningún F(m) con m < n, entonces se dice que p es un factor característico o un divisor primitivo de F(n). El teorema de Carmichael establece que cada número de Fibonacci, con las únicas excepciones anteriormente mencionadas, tiene al menos un factor característico.



No hay comentarios:
Publicar un comentario