teorema de Fermat -no confundir con el último teorema de Fermat-, afirma que:
|
Suele utilizarse como método para hallar máximos y mínimos locales de funciones diferenciablesen intervalos abiertos, ya que todos ellos son puntos estacionarios de la función (puntos donde lafunción derivada vale cero,  ). El teorema de Fermat sólo da una condición necesariapara los máximos y mínimos locales, sin embargo, no se refiere a otra clase de puntos estacionarios como son en ciertos casos los puntos de inflexión (que no son ni máximos ni mínimos). La derivada segunda de la función (
). El teorema de Fermat sólo da una condición necesariapara los máximos y mínimos locales, sin embargo, no se refiere a otra clase de puntos estacionarios como son en ciertos casos los puntos de inflexión (que no son ni máximos ni mínimos). La derivada segunda de la función ( ) -si es que existe- puede indicar si el punto estacionario en cuestión es un máximo, un mínimo, o un punto de inflexión. El teorema de Fermat es un teorema de análisis real llamado así en honor a Pierre de Fermat.
) -si es que existe- puede indicar si el punto estacionario en cuestión es un máximo, un mínimo, o un punto de inflexión. El teorema de Fermat es un teorema de análisis real llamado así en honor a Pierre de Fermat.
 ). El teorema de Fermat sólo da una condición necesariapara los máximos y mínimos locales, sin embargo, no se refiere a otra clase de puntos estacionarios como son en ciertos casos los puntos de inflexión (que no son ni máximos ni mínimos). La derivada segunda de la función (
). El teorema de Fermat sólo da una condición necesariapara los máximos y mínimos locales, sin embargo, no se refiere a otra clase de puntos estacionarios como son en ciertos casos los puntos de inflexión (que no son ni máximos ni mínimos). La derivada segunda de la función ( ) -si es que existe- puede indicar si el punto estacionario en cuestión es un máximo, un mínimo, o un punto de inflexión. El teorema de Fermat es un teorema de análisis real llamado así en honor a Pierre de Fermat.
) -si es que existe- puede indicar si el punto estacionario en cuestión es un máximo, un mínimo, o un punto de inflexión. El teorema de Fermat es un teorema de análisis real llamado así en honor a Pierre de Fermat.
teorema de Fermat sobre la suma de dos cuadrados establece la relación que hay entre los números primos representables como suma de dos cuadrados. En concreto, el teorema dice lo siguiente:
|
O sea, p = x2+y2, donde x e y son números enteros si p =4k+1 para algún k entero, o escrito en notación moderna, p ≡ 1 (mod 4) (véase aritmética modular).
El teorem
Por ejemplo Fermat anunció su teorema en una carta a Marin Mersenne fechada el 25 de diciembre de 1640, razón por la cual se le conoce también como Teorema de navidad de Fermat.1
Como era habitual en Fermat, éste no dio ninguna demostración de su teorema y fue Leonhard Euler, tras mucho esfuerzo, el primero que dio una demostración formal basada en descenso infinito. Fue anunciada en una carta escrita a Christian Goldbach el 12 de abril de 1749.2 Lagrange publicó una demostración en 1775 basada en su estudio de formas cuadráticas. Esta demostración fue simplificada porGauss en su libro Disquisitiones arithmeticae.3 Dedekind dio otras dos demostraciones basadas en la aritmética de los enteros gaussianos. Hay incluso una demostración elegante usando el teorema de Minkowski sobre conjuntos convexos.a es también conocido como lema de Thue, debido al matemático noruego Axel Thue.
Por ejemplo, los números primos 5,13,41,61 son de la forma 4k+1, y por el teorema pueden ser escritos como suma de dos cuadrados de la siguiente manera:
Fermat anunció otros resultados relacionados catorce años más tarde. Así, en una carta escrita a su amigo Blaise Pascal el 25 de septiembre de 1654, anunciaba los siguientes resultados para números primos mayores que 2:4
- Cada número primo, que es mayor en una unidad a un múltiplo de 3, está compuesto por un cuadrado y el triple de otro cuadrado como 7, 13, 19, 31, 37, ...
- Cada número primo, que es mayor en una unidad( 1 ) o en tres unidades(3) a un múltiplo de 8, está compuesto por un cuadrado y el doble de otro cuadrado como 11, 17, 19, 41, 43, ...
Pierre de Fermat
Lo que en términos modernos viene a ser:
teorema del número poligonal de Fermat dice que cada número natural es suma de a lo máximo n números poligonales. Cada número natural puede ser escrito como la suma de tres o menos números triangulares, o cuatro o menos números cuadrados, o cinco o menos números pentagonales, y así sucesivamente. 17, por ejemplo, puede ser escrito como sigue:
- 17 = 10 + 6 + 1 (números triangulares)
- 17 = 16 + 1 (números cuadrados)
- 17 = 12 + 5 (números pentagonales).
Un caso especial del teorema bien conocido es el teorema de los cuatro cuadrados de Lagrange, que asegura que cada número natural puede ser expresado como la suma de cuatro cuadrados, por ejemplo, 7 = 4 + 1 + 1 + 1.
Joseph Louis Lagrange demostró el caso cuadrado en 1770 y Carl Friedrich Gauss demostró el caso triangular en 1796, pero el teorema no fue resuelto de forma general hasta que al final fue demostrado por Cauchy en 1813. Una demostración de Nathanson (ver referencias) está basada en el siguiente lema dado por Cauchy:
Para números naturales impares  y
y  tales que
tales que  y
y  se pueden encontrar números enteros no negativos
se pueden encontrar números enteros no negativos  y
y  tales que
tales que  y
y 
 y
y  tales que
tales que  y
y  se pueden encontrar números enteros no negativos
se pueden encontrar números enteros no negativos  y
y  tales que
tales que  y
y 
último teorema de Fermat, o teorema de Fermat-Wiles, es uno de los teoremas más famosos en la historia de la matemática. Utilizando la notación moderna, se puede enunciar de la siguiente manera:
|
El teorema fue conjeturado por Pierre de Fermat en 1637, pero no fue demostrado hasta 1995por Andrew Wiles ayudado por el matemático Richard Taylor. La búsqueda de una demostración estimuló el desarrollo de la teoría algebraica de números en el siglo XIX y la demostración delteorema de la modularidad en el siglo XX.
Teorema de Fitting es un teorema matemático demostrado por Hans Fitting. Se puede establecer de la siguiente manera:
- Si M y N son un subgrupo normal nilpotente de un grupo G, entonces su producto MN es también un subgrupo normal nilpotente deG; Si, además, M es nilpotente de clase m y N es nilpotente de clase n, entonces MN es nilpotente de clase a lo sumo m + n.
Por inducción se deduce también que el subgrupo generado por una colección finita de subgrupos normales nilpotentes es nilpotente. Sin embargo, un subgrupo generado por una colleción infinita de subgrupos normales nilpotentes no tiene que ser nilpotente.
En terminos de la teoría del orden, parte del teorema de Fitting puede afirmar que:
- El conjunto de subgrupos normales nilpotentes forman un subgrupo de retículos.
Por lo tanto, el subgrupo normal nilpotente de un grupo finito también forma un retículo limitado, y tiene un elemento superior, el subgrupo Fitting.
Sin embargo, subgrupos normales nilpotentes no forman un retículo completo, como un subgrupo generado por una colección infinita de subgrupos normales nilpotentes no necesariamente son nilpotentes, aunque será normal. La unión de todos los subgrupos normales nilpotentes todavía está definido como el subgrupo Fitting, pero no necesariamente nilpotente.







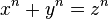
No hay comentarios:
Publicar un comentario