AMIGOS PARA SIEMPRE: Geometría

Ad Triangulum es método constructivo que relaciona la geometría con la arquitectura en un sistema de proporciones, concretamente es empleado en el diseño arquitectónico de estilos clásicos como el gótico tardío y del renacimiento.¹ Mientras que en el método "ad quadratum" la altura del edificio sería igual a su anchura, en el caso de aplicar el método "ad triángulum" la altura es inferior a la anchura del mismo. De esta forma la seccción del edificio se inscribe en un triángulo, que en la mayoría de los casos pretende ser equilátero (la proporción

1:2(\sqrt{3})

). En la antigüedad la elección de la forma constructiva era objeto de debate entre expertos, y en muchas ocasiones se elegía una u otra por criterios poco científicos.

Un ejemplo constructivo ad triangulum es la catedral de Milán.

Proporciones existentes en untriángulo equilátero.

Características

En el diseño constructivo mediante "ad triangulum" se procede fundamentalmente mediante triangulación. Empleando en su diseño y ubicación las relaciones métricas en el triángulo. Los triángulos más empleados eran el equilátero, el sagrado egipcio, elrectángulo y el pitagórico. En el triángulo más empleado en construcción, el equilátero, la relación proporcional entre uno de sus lados y la altura es de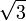

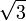\sqrt{3}

, que es un número irracional y por lo tanto, incómodo de manipular en la matemática medieval.

Usos

Se empleaba el método "ad triangulum" en el diseño de catedrales góticas en las que era una forma más intuitiva de ponercontrafuertes al empuje de las bóvedas de crucería. El problema era manipular los múltiplos y sub-múltiplos de la raíz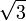

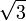\sqrt{3}

. Un ejemplo de catedral diseñada de esta forma es la Catedral de Milán que comenzó diseñándose como "ad quadratum" y durante su construcción se cambió el diseño a "ad triangulum" mediante consenso de catorce maestros arquitectos de la época.² Otros ejemplos en España son la Catedral de Santa María de la Asunción de Barbastro en Huesca, la Catedral Nueva de Salamanca.

La altura de un objeto o figura geométrica es una longitud o una distancia de una dimensión geométrica, usualmente vertical o en la dirección de la gravedad. Este término también se utiliza para designar la coordenada vertical de la parte más elevada de un objeto.

Coloquialmente, el sustantivo «altura» puede ser reemplazado por «alto» (adjetivo sustantivizado), que la Real Academia Española acepta como vigesimotercera acepción en su Diccionario.

8Enlaces externos

Altura en el plano coordenado

En coordenadas cartesianas (x, y), en el plano, la altura se refiere a la distancia perpendicular al eje X, o la longitud o distancia entre un vértice y el lado opuesto (o su prolongación), denominado «base» si está en posición horizontal. La altura siempre es perpendicular a la base. Un triángulo tiene tres alturas diferentes respecto de sus tres lados y vértices.

Altura en figuras geométricas planas

En el plano, la altura de una figura geométrica relativa a un lado, considerado como horizontal, es la distancia que hay desde el punto más alto de la figura hasta dicho lado.

En un paralelogramo, la altura es la menor distancia entre lados paralelos.

En un cuadrilátero con al menos dos lados paralelos, la altura es la menor distancia entre los dos lados paralelos.

Alturas de un triángulo

La altura de un triángulo respecto de un lado es la recta o segmento perpendicular a dicho lado o a su prolongación y que pasa por el vértice opuesto, y por extensión, longitud de dicho segmento.²

Definición

La altura de un triángulo es el segmento de perpendicular trazado desde un vértice hasta el lado opuesto o la prolongación del mismo. ³

Nomenclatura

La intersección de la altura y el lado opuesto o prolongación en su caso se denomina «pie» de la altura.

Se llama altura de un triángulo a la distancia que hay entre un lado y el vértice opuesto.

La magnitud de la altura sirve para calcular el área de un triángulo, siendo su valor: a = b·h/2, donde a es el área, b la base –la longitud del lado "inferior"–, y h su altura correspondiente.

Ésta fórmula se puede demostrar, geométricamente, trazando un rectángulo cuya área es el doble del área del triángulo, con la misma base.

Características y propiedades

En todo triángulo:

Al menos una de las alturas se encuentra dentro del triángulo;
La altura de mayor longitud es la correspondiente a la del lado menor del triángulo;
Las tres alturas se cortan en un punto, llamado ortocentro del triángulo;
La suma de las tres alturas de todo triángulo es menor que el perímetro de este.⁴

Cálculo de las alturas de un triángulo

Para un triángulo ΔABC cualquiera, conociendo la longitud de sus lados (a, b, c), se pueden calcular las respectivas longitudes de las alturas (h_a, h_b, h_c) aplicando las siguientes fórmulas:

$h_{a}=\frac{\tau }{a}$

$h_{b}=\frac{\tau }{b}$

$h_{c}=\frac{\tau }{c}$

Donde h_a es la altura correspondiente al lado a, h_b es la altura correspondiente al lado b, h_c es la altura correspondiente al lado c y el término

\tau

es:

\tau =\frac{1}{2} \sqrt{(a+b-c) (a-b+c) (-a+b+c) (a+b+c)}

h_a = \frac{2}{a} \sqrt{p(p-a)(p-b)(p-c)}

;

h_b = \frac{2}{b} \sqrt{p(p-a)(p-b)(p-c)}

;

h_c = \frac{2}{c} \sqrt{p(p-a)(p-b)(p-c)}

⁵

Altura en tres dimensiones

Esquema elemental de posicionamiento espacial, consistente en un marco de referencia respecto a un origen dado.

La altura de un objeto o figura geométrica es una longitud o una distancia, usualmente vertical o en la dirección de la gravedad. Este término también se usa para designar la coordenada vertical de la parte más elevada de un objeto.

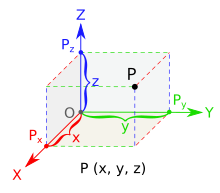
En coordenadas cartesianas (x, y, z), la altura de los volúmenes corresponde a la coordenada Z que es la que se sitúa perpendicular al suelo (vertical), normalmente, ya que X e Y son asignados a valores horizontales: anchura (o ancho) y longitud(o largo).

Altura de sólidos

La altura de una pirámide es la distancia del vértice al plano de la base. En el caso del tetraedro, que es un caso especial de pirámide, hay cuatro alturas; partiendo cada una de cada vértice.

Altura en otros contextos

En simulación 3D

El color verde representa al eje Z.
En las Normal Maps (un sistema que simula superficies de detalle por medio de colores) la base azul representa el valor 0 (base). La X (±1) representa el color rojo, y la Y (±1) representa el azul, que da los valores de elevación (RGB)

La altura de un triángulo es el segmento perpendicular a un lado que va desde el vértice opuesto a este lado (o a su prolongación). También puede entenderse como la distancia de un lado al vértice opuesto.

Hay tres alturas (h_a, h_b y h_c), según a que lado está asociada dicha altura. A partir de la fórmula de Herón, conociendo los tres lados (a, b y c), se pueden hallar las tres alturas:

Fórmula de las tres alturas del triángulo.

Dibujo de las tres alturas de un triángulo y del ortocentro.

Las tres alturas del triángulo (o sus prolongaciones) se cortan en un punto llamadoortocentro (H).

Las alturas podrían estar en el exterior del triángulo, en el caso de que sea untriángulo obtusángulo. El ortocentro también será exterior en los triángulos obtusángulos. En los rectángulos coincidirá con el vértice del ángulo recto. En losacutángulos, será un punto interior.

Altura del triángulo equilátero

Dibujo del triángulo equilátero para el cálculo de su altura

La altura (h) del triángulo equilátero se puede calcular a partir del teorema de Pitágoras. Los lados a, a/2 y h forman un triángulo rectángulo. Los costados a/2 y h son los catetos y a lahipotenusa.

Aplicando el teorema de Pitágoras:

Cálculo de la altura del triángulo equilátero.

Y obtenemos que la altura (h) del triángulo equilátero es:

Fórmula de la altura del triángulo equilátero.

Dibujo del triángulo equilátero para el cálculo de su altura por razones trigonométricas.

Otro procedimiento para calcular su altura sería a partir de las razones trigonométricas.

Respecto al ángulo de 60º, la razón entre la altura h y la hipotenusa del triángulo a es igual alseno de 60º. Por tanto:

Cálculo de la altura del triángulo equilátero por razones trigonométricas.

Altura del triángulo isósceles

Dibujo del triángulo isósceles para el cálculo de su altura

La altura (h) del triángulo isósceles se puede calcular a partir del teorema de Pitágoras. Los lados a, b/2 y h forman un triángulo rectángulo. Los costados b/2 y h son los catetos y a lahipotenusa.

Por el teorema de Pitágoras: