martes, 1 de marzo de 2016

Matemáticas - Matrices

En álgebra lineal, una Matriz antihermitiana es una matriz cuadrada cuya traspuesta conjugada es menos la matriz. Esto es si satisface a la relación:

A^*

= -A

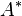
o en su forma componente, si (

A=a_{i,j}

a_{i,j} = -\overline{a_{j,i}}

Para todas las i y las j.

Ejemplo

Por ejemplo, la siguiente matriz es una matriz antihermitiana:

\begin{pmatrix}i & 2 + i \\ -2 + i & 3i \end{pmatrix}

Propiedades

1. Los autovalores de una matriz antihermitiana son todos imaginarios puros. Es más, las matrices antihermitianas son matrices normales. Por lo tanto, son diagonalizables y sus autovectores para distintos autovalores son ortogonales.
2. Si A es antihermitiana entonces iA es hermitiana.
3. Si A,B es antihermitiana, entonces aA+bB es antihermitiana para todos los escalares reales de a,b.
4. Si A es antihermitiana, entonces A^2k es hermitiana para todos los naturales k.
5. Si A es antihermitiana, entonces A^2k+1 es antihermitiana para todos los naturales k.
6. Si A es antihermitiana, entonces e^A es matriz unitaria.
7. La diferencia entre una matriz y su traspuesta conjugada ( $C - C^*$ ) es antihermitiana.
8. Una matriz cuadrada arbitraria C puede ser escrita como la suma de la matriz hermitiana A y la matriz antihermitiana B:

C = A+B \quad\mbox{para}\quad A = \frac{1}{2}(C + C^*) \quad\mbox{y}\quad B = \frac{1}{2}(C - C^*).

Matriz antihermitiana

En algebra lineal, una Matriz antihermitiana es una matriz cuadrada cuya traspuesta conjugada es menos la matriz. Esto es si satisface a la relación:

A *

= -A
o en su forma componente, si (

A = a i, j

external image 085b265ea1f38e78e14e271e22e22d30.png

Para todas las i y las j.

Ejemplo:

Por ejemplo, la siguiente matriz es una matriz antihermitiana:

external image 58d1bc851eac761ba57faf9f5e084493.png

Matrices hermitianas y antihermitianas

Definición

Sea A una matriz de n x n con elementos en C. Se dice que:

1) A es hermitiana si

Donde los elementos de la matriz deben ser simétricos y conjugados con respecto a la diagonal principal y esta debe estar

compuesta únicamente por números reales.

2) A es antihermitiana si

Donde los elementos de la matriz deben ser simétricos y solo deben diferir  en  el  signo de la parte real  con respecto  a su
diagonal principal, es decir sus partes imaginarias deben ser exactamente  iguales,  además la diagonal  principal debe  estar
compuesta de números imaginarios.

Teorema

Sea A una matriz de m x n con elementos en C, entonces:

es hermitiana