matriz de adjuntos o matriz de cofactores cof(A) es la resultante de sustituir cada término aij de A por el cofactor aij de A. El término matriz adjunta adj(A) suele crear confusión, ya que en muchos tratados clásicos sobre álgebra lineal corresponde a la matriz de cofactores traspuesta,1 2 3 sin embargo, en otros textos, se corresponde a la matriz de cofactores, puesto que llaman de la misma manera adjunto al cofactor y de ahí que sea adjunta.4 5 Aparte, también se utiliza el símbolo adj( ) indistintamente a cof( ) para el cálculo en los elementos de una matriz, haciendo, si cabe, la confusión más amplia.6
El interés principal de la matriz adjunta es que permite calcular la inversa de una matriz, ya que se cumple la relación:
donde adj(A) corresponde a la matriz de cofactores traspuesta, o sea,
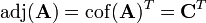 .
.
Sin embargo, para matrices de dimensiones grandes, este tipo de cálculo resulta más costoso, en términos de operaciones, que otros métodos como el método de eliminación de Gauss.
Definición y fórmulas de cálculo
Esta definición no permite calcular directamente la matriz de adjuntos (o cofactores) por lo que comúnmente se define también la matriz de adjuntos mediante la siguiente fórmula explícita. Dadas las componentes explícitas de la matriz:  para cada i y j se define la matriz
para cada i y j se define la matriz  como la matriz de orden
como la matriz de orden  obtenida a partir de
obtenida a partir de  eliminando la fila i-ésima y la columna j-ésima. Y se define la cantidad:
eliminando la fila i-ésima y la columna j-ésima. Y se define la cantidad:
 para cada i y j se define la matriz
para cada i y j se define la matriz  como la matriz de orden
como la matriz de orden  obtenida a partir de
obtenida a partir de  eliminando la fila i-ésima y la columna j-ésima. Y se define la cantidad:
eliminando la fila i-ésima y la columna j-ésima. Y se define la cantidad:
Y se tiene que estas son precisamente las componentes de la matriz de adjuntos (o cofactores), es decir, 

Matrices 2 x 2
Dada una matriz de 2 x 2:
Su matriz adjunta viene dada por:
donde C es la matriz de cofactores.
Matrices 3 x 3
Dada una matriz de 3 x 3:
Su matriz de cofactores viene dada por:
y por lo tanto la transpuesta de la matriz de cofactores es la matriz Adjunta:
Para matrices de 3x3 también puede usarse la siguiente fórmula:
Ejemplo
Un ejemplo sería el siguiente:
Matrices n x n
Para matrices con n grande, el costo computacional del cálculo de adjuntos es grande, por lo que si el objetivo es calcular la inversa de una matriz, se recurre a otros algoritmos de cálculo que no impliquen calcular primero la matriz de adjuntos. Para el cálculo de la matriz de adjuntos en el caso general, puede emplearse la siguiente fórmula:
Propiedades
Dada una matriz  definiendo
definiendo  puede probarse que las
puede probarse que las  pueden escribirse como suma de monomios de grado n en las componentes
pueden escribirse como suma de monomios de grado n en las componentes  . Eso hace que a medida que n aumenta el cálculo de la matriz adjunta por aplicación de fórmulas directas sea complicado, llegando a ser computacionalmente muy costoso.
. Eso hace que a medida que n aumenta el cálculo de la matriz adjunta por aplicación de fórmulas directas sea complicado, llegando a ser computacionalmente muy costoso.
 definiendo
definiendo  puede probarse que las
puede probarse que las  pueden escribirse como suma de monomios de grado n en las componentes
pueden escribirse como suma de monomios de grado n en las componentes  . Eso hace que a medida que n aumenta el cálculo de la matriz adjunta por aplicación de fórmulas directas sea complicado, llegando a ser computacionalmente muy costoso.
. Eso hace que a medida que n aumenta el cálculo de la matriz adjunta por aplicación de fórmulas directas sea complicado, llegando a ser computacionalmente muy costoso.
Si consideramos la operación de buscar la matriz adjunta como una función:  resulta que esa función es continua. Esto puede verse a partir de la continuidad de la función determinante. Además se tienen otras propiedades interesantes:
resulta que esa función es continua. Esto puede verse a partir de la continuidad de la función determinante. Además se tienen otras propiedades interesantes:
 resulta que esa función es continua. Esto puede verse a partir de la continuidad de la función determinante. Además se tienen otras propiedades interesantes:
resulta que esa función es continua. Esto puede verse a partir de la continuidad de la función determinante. Además se tienen otras propiedades interesantes:
 8
8
 para
para  .
. para
para  .
. para
para  .
. para
para  .
. .
.
Si p(t) = det(A − tI) es el polinomio característico de A y definimos el polinimio q(t) = (p(0) − p(t))/t, entonces:
Donde  son los coeficientes de p(t):
son los coeficientes de p(t):
 son los coeficientes de p(t):
son los coeficientes de p(t):
ADJUNTO DE UNA MATRIZ
Consideremos una matriz n-cuadrada A = (ai j ) sobre un cuerpo K. El adjunto de A, denotado por adj A, es la traspuesta de la matriz de cofactores de A:
Ejemplo:
Los cofactores de los nueve elementos de A son:
La traspuesta de la matriz de los cofactores anteriores proporciona el adjunto de A:
· Aplicación del adjunto para hallar la matriz inversa
Para toda matriz cuadrada A,
A·(adj A) = (adj A) · A = |A|I
De este modo, si |A| ¹ 0,
Observemos que esta propiedad nos permite hallar por otro método la inversa de una matriz.
Ejemplo:
Consideremos la matriz
y el det A:
Así pues, aplicando la propiedad anterior:
Ejercicio:
Calcular, por la propiedad anterior, la inversa de las siguientes matrices:
a)
b)
a) Primero hallaremos el determinante de la matriz A:
El siguiente paso es hallar el adjunto de la matriz B, así pues, los cofactores de los cuatro elementos de B son:
B11 = 5 B12 = -2
B21 = 1 B22= 3
y el adjunto de B, denotado por adj B, será
b) Empezaremos por hallar el det A,
Los cofactores de los nueve elementos de A son:
La traspuesta de la matriz de los cofactores anteriores proporciona el adjunto de A:
Aplicando la propiedad de la matriz inversa obtenemos A-1:
|
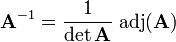
 su matriz de adjuntos es la única matriz
su matriz de adjuntos es la única matriz  tal que:
tal que:






![[\mbox{adj}(\mathbf{A})]_{ij} =
\frac{1}{2} \; \epsilon_{mni} \; \epsilon_{pqj} \; a_{mp} \; a_{nq}](https://upload.wikimedia.org/math/4/e/a/4eacf68bd6a995c65d737d3bca21367b.png)

![[\mbox{adj}(\mathbf{A})]_{ij} =
\frac{1}{(n-1)!} \;
\epsilon_{i_1 \dots i_{n-1} i} \;
\epsilon_{j_1 \dots j_{n-1} j} \;
a_{i_1 j_1} \;
a_{i_2 j_2} \;
\dots \;
a_{i_{n-1} j_{n-1}}](https://upload.wikimedia.org/math/6/a/8/6a8104e97c0185b417cf2f99f6b1e724.png)



Buena explicación, muchas gracias.
ResponderEliminar