martes, 1 de marzo de 2016

Matemáticas - Matrices


matriz cero o matriz nula es una matriz con todos sus elementos iguales a cero. Algunos ejemplos de matrices nulas son:
0_{1,1} = \begin{bmatrix} 0 \end{bmatrix} ,\ 0_{2,2} = \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} ,\ 0_{2,3} = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} , \mbox{etc.}\
Por lo tanto, una matriz nula de orden mxn definida sobre un anillo K asume la forma:
0_{K_{m,n}} = \begin{bmatrix} 0_K & 0_K & \cdots & 0_K \\ 0_K & 0_K & \cdots & 0_K \\ \vdots & \vdots & & \vdots \\ 0_K & 0_K & \cdots & 0_K \end{bmatrix}_{m \times n}
Una matriz cero es, al mismo tiempo, matriz simétrica, matriz antisimétrica, matriz nilpotente y matriz singular.

A zero matrix is an m×n matrix consisting of all 0s (MacDuffee 1943, p. 27), denoted 0. Zero matrices are sometimes also known as null matrices (Akivis and Goldberg 1972, p. 71).
A zero matrix is the additive identity of the additive group of m×n matrices. The matrix exponential of 0 is given by the identity matrix I. An m×n zero matrix can be generated in the Wolfram Language as ConstantArray[0, {m, n}].











Una Matriz conjugada es el resultado de la sustitución de los elementos de una matriz A por sus conjugadas. Es decir, la parte imaginaria de los elementos de la matriz cambia su signo.

A = \begin{pmatrix} 2+i & 3 & -1+4i \\ 4-i & 5 & -2-2i \\ 1 & 3-i & 1+3i \end{pmatrix}, \overline{A} = \begin{pmatrix} 2-i & 3 & -1-4i \\ 4+i & 5 & -2+2i \\ 1 & 3+i & 1-3i \end{pmatrix}



Una Matriz conjugada es el resultado de la sustitución de los elementos de una matriz A por sus valores conjugados. Es decir, la parte imaginaria de los elementos de la matriz cambian su signo.
Ejemplo de matrices conjugadas
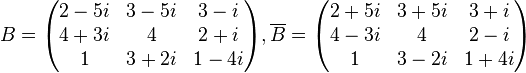
B = \begin{pmatrix} 2-5i & 3-5i & 3-i \\ 4+3i & 4 &2+i \\ 1& 3+2i & 1-4i \end{pmatrix}, \overline{B} = \begin{pmatrix} 2+5i & 3+5i & 3+i \\ 4-3i & 4 & 2-i\\ 1 & 3-2i & 1+4i\end{pmatrix}









 matriz cuadrada si el número de filas es igual al número columnas, es decir, n = m y se dice, entonces que la matriz es de orden n:
A = \begin{pmatrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1n} \\ a_{21} & a_{22} & a_{23} & \cdots & a_{2n} \\ a_{31} & a_{32} & a_{33} & \cdots & a_{3n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & a_{n3} & \cdots & a_{nn} \\ \end{pmatrix}
Las matrices cuadradas son las más utilizadas en álgebra.

Propiedades

Toda matriz cuadrada se puede descomponer en la suma de una matriz simétrica y una matriz antisimétrica.
Si A y B son matrices del mismo orden, entonces se pueden sumar entre sí. Los productos de matrices son válidos en ambos sentidos, AB y BA. Además, surgen los conceptos de determinante y traza solo aplicables a matrices cuadradas.
Una matriz cuadrada A de orden n es singular si su determinante es nulo. En tal caso se dice que dicha matriz no tiene inversa.

Ejemplo

Ejemplo de matriz cuadrada para n = 3:
\begin{pmatrix} 1 & -3 & 8 \\ 2 & 0 & 0 \\ 0 & 1 & -1 \end{pmatrix}




La matriz cuadrada tiene el mismo número de filas que de columnas.
Los elementos de la forma aii constituyen la diagonal principal.
La diagonal secundaria la forman los elementos con i+j = n+1.
Cuadrada
Publicado por en

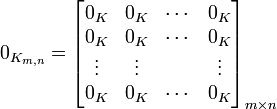
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)