sábado, 13 de febrero de 2016

EPÓNIMOS

Epónimos relacionados con la economía


Modelo de crecimiento de Solow, conocido como el modelo exógeno de crecimiento o modelo de crecimiento neoclásico, es un modelo macroeconómico creado para explicar el crecimiento económico y las variables que inciden en este en el largo plazo. El modelo se remonta a los trabajos de Robert Solow (1924- ).

Explicación intuitiva

El modelo de Solow pretende explicar cómo crece la producción nacional de bienes y servicios mediante un modelo cuantitativo. En el modelo intervienen básicamente la producción nacional (Y), la tasa de ahorro (s) y la dotación de capital fijo (K). El modelo presupone que el Producto interno bruto (PIB) nacional es igual a la renta nacional (es decir, se supone una "economía cerrada" y que por tanto no existen importaciones ni exportaciones).
La producción por otra parte dependerá de la cantidad de mano de obra empleada (L) y la cantidad de capital fijo, (es decir, maquinaria, instalaciones y otros recursos usados en la producción) y la tecnología disponible (si la tecnología mejorara con la misma cantidad de trabajo y capital podría producirse más, aunque en el modelo se asume usualmente que el nivel de tecnología permanece constante). El modelo presupone que la manera de aumentar el PIB es mejorando la dotación de capital (K). Es decir, de lo producido en un año una parte es ahorrada e invertida en acumular más bienes de capital o capital fijo (instalaciones, maquinaria), por lo que al año siguiente se podrá producir una cantidad ligeramente mayor de bienes, ya que habrá más maquinaria disponible para la producción.
En este modelo el crecimiento económico se produce básicamente por la acumulación constante de capital, si cada año aumenta la maquinaria y las instalaciones disponibles (capital fijo) para producir se obtendrán producciones progresivamente mayores, cuyo efecto acumulado a largo plazo tendrá un notable aumento de la producción y, por tanto, un crecimiento económico notorio.
Entre las predicciones cualitativas del modelo está que el crecimiento basado puramente en la acumulación de capital, sin alterar la cantidad de mano de obra ni alterar la tasa de ahorro es progresivamente más pequeño, llegándose a un estado estacionario en que no se produce más crecimiento y las inversiones compensan exactamente la depreciación asociada al desgaste del capital fijo.

Formulación matemática

El modelo busca encontrar las variables relevantes que ocasionan el crecimiento económico de un país (economía cerrada), en cuanto algunas ayudan a mejorar la situación solo en el corto plazo, y otras, que afectan a las tasas de crecimiento del largo plazo. Se toman todas las variables que el modelo considera como significativas en el proceso de crecimiento, como exógenas, pero muestra la incidencia de estas en el proceso de crecimiento. El modelo utiliza la función de producción Cobb-Douglas en la siguiente forma (aunque se puede por supuesto plantear también referido a la Productividad Total de los Factores):1
(1a)Y=K^\alpha (AL)^{1-\alpha}\,
Definiendo las variables, tenemos que:
K\, = Capital total
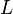L\, = fuerza laboral o trabajo total usado en la producción.
A\, = es una constante matemática que representa la tecnología asociada al factor trabajo.1
Y\, = Producción total [medida por ejemplo en unidades monetarias].
\alpha\, = Fracción del producto producida por el capital, o coeficiente de los rendimientos marginales decrecientes.
Se sabe, por otro lado, que necesariamente \scriptstyle 0<\alpha<1\,, se puede probar que α coincide con la participación total del capital en la producción (de acuerdo con el análisis de la productividad total de los factores). Si alfa es α ~ 1, la producción se basará fundamentalmente en el capital disponible y será casi independiente de la mano de obra. Existen razones para suponer que para muchas situaciones reales la función de producción de Cobb-Douglas es una función creíble de producción que tiene retornos constantes a escala, y rendimientos marginales decrecientes al capital y al trabajo. Más adelante se verá que si se supone que la función de producción es de este tipo, existe la posibilidad de convergencia a un producto estacionario que deja de crecer mediante la tasa de ahorro.
Técnicamente la hipótesis de que la función de producción es la función de Cobb-Douglas no es fundamental para el modelo, porque bastaría que fuera una función monótona creciente en el capital y la cantidad de trabajo.
Para formular el modelo a partir de la función de Cobb-Douglas se definen por conveniencia:
  • el producto per cápita efectivo y como la cantidad de producción por unidad de mano de obra y
  • el stock de capital per cápita efectivo k como la cantidad de capital por unidad de mano de obra
Es decir, definimos las variables:
(2)y:= \frac{Y}{AL}, \qquad k :=\frac{K}{AL}
Como hemos supuesto que la función de producción es de tipo Cobb-Douglas se tiene la siguiente relación entre y y k:
(1b)y = \frac{K^\alpha (AL)^{1-\alpha}}{AL} = \frac{K^\alpha}{(AL)^\alpha}= k^\alpha = f(k)
Asumiendo el producto per cápita efectivo y en la función anterior, tendremos que mientras menor sea α habrá un producto per cápita efectivo cada vez menor, es decir, la función toma la forma de una raíz, aunque la función es divergente al infinito si k tiende al infinito. La función anterior satsiface las condiciones de Inada, a saber:
\lim_{k \to \infty} f'(k) = 0, \qquad \lim_{k \to 0} f'(k)=\infty
Estos límites son conocidos como las condiciones de Inada, y explican que la derivada de \scriptstyle f(k), es decir, el producto marginal del capital es 0 cuando k es alto. Además explica que cuando k es demasiado bajo, el producto marginal es muy alto. Estas últimas condiciones, aunque bastante evidentes matemáticamente, posteriormente implicarán que países con una cantidad de capital baja crecerían a tasas altas, mientras que países con altas cantidades de capital crecerían a tasas más bajas, debido a los rendimientos marginales decrecientes de este.

Ecuaciones relevantes del modelo de Solow

Existe una ecuación relevante del modelo de Solow, y es la ecuación de acumulación de capital.
(4)\dot{K}_t = \frac{\part K_t}{\part t} = sY_t - K_t\delta \,
Donde
s\, = Tasa de ahorro
Y_t\, = Producto de la economía en el período t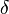
\delta\, = tasa de depreciación del capital existente.
K_t\, = Capital total en el período t
El término sY\, representa la inversión efectiva en capital que puede realizar la economía, que es el producto multiplicado por la tasa de ahorro (ya que el modelo presupone que todo el ahorro se invierte). El segundo término de la ecuación \delta K\, representa la inversión de reposición (o gastos de amortización) que representa cuanto capital ya no sirve o es inútil para la acumulación de capital. Para analizar más la inversión de reposición, es necesario determinar esta misma ecuación en términos per cápitas y efectivos.
Para calcular el incremento de stock de capital per cápita, derivando, usando la regla de la cadena y substiyendo el la ecuación resultante el resultado (4) se tiene:
(5)\dot{k} = \frac{\part}{\part t}\left(\frac{K}{AL}\right) = \frac{\dot{K}_t}{A_tL_t} - \frac{K_t}{A_tL_t^2}\dot{L}_t - \frac{K_t}{A_t^2L_t}\dot{A}_t = \frac{sY}{AL} - \frac{K}{AL} \left( \delta + \frac{\dot{A}}{A} + \frac{\dot{L}}{L} \right) = sy - (\delta + g+ n)k
Donde:
n:= \Delta L/L\,
g:= \Delta A/A\,
Esta última ecuación tiene el mismo aspecto que (4), pero en términos per cápita, con una inversión de reposición igual a \scriptstyle (\delta +n)k, que muestra la cantidad de inversión necesaria para mantener el capital constante. Aumentos de depreciación, tendrían efectos de disminución de la acumulación de capital, y por lo tanto, un menor [estado estacionario] del capital. Aumentos en la tasa de crecimiento de la población, causarían un aumento menor o disminución de la acumulación de capital per cápita efectivo.
Es necesario que la inversión efectiva pueda sostener los movimientos o la depreciación misma, así como el crecimiento de la población y la nueva tecnología que necesitan inversión física para producirla. Si tenemos altas tasas de crecimiento de la población, es difícil que el capital per cápita efectivo crezca, ya que habrá menor maquinaria para repartir entre los nuevos individuos potencialmente productivos que entran al mercado. Así también, aumentos de la tasa de tecnología necesitan producir nueva maquinaria, por lo que es necesario que haya inversión efectiva para sostener aumentos de la tecnología.

Equilibrio del estado estacionario

Diagrama del modelo de crecimiento de Solow.
El equilibrio estacionario es la condición del modelo en que finaliza el aumento del capital reflejado en la ecuación de acumulación de capital per cápita, que termina con un capital fijo sin variaciones adicionales.
\begin{cases} \dot{k} =0 \\ sy = (n+g+\delta)k \\ y=f(k) \end{cases}
Como se supone que la función \scriptstyle f(\cdot) el sistema anterior tendrá una solución única \scriptstyle (y^*,k^*) y los niveles de renta per cápita efectiva, capital per cápita efectivo, tasa de ahorro, tasa de cambio tecnológico y tasa de depreciación del mismo determinan el llamado estado de equilibrio o estado estacionario del modelo de Solow.
El equilibrio en el modelo de Solow es la senda de la convergencia de los países: una economía, mediante la propiedad de rendimientos marginales decrecientes, tiende a decrecer su producción marginal; o dicho en otros términos, la producción total cada vez crece menos. Por lo que \scriptstyle sy tiende también a crecer menos, lo que eventualmente hace que se iguale a \scriptstyle (n+g+\delta)k. Esta condición mantiene el stock de capital per cápita efectivo constante, sin variaciones. Sin embargo, en estado estacionario, es posible afirmar que el producto per cápita crece a la tasa de crecimiento de la tecnología, y el producto total crece a la tasa de crecimiento de la población y de la tecnología. El aporte de estas variables exógenas logran explicar el crecimiento en el largo plazo, es decir, cuando la economía alcanza su capital estacionario.
Este es el gráfico principal del modelo de Solow, y muestra que en el equilibrio de largo plazo, \scriptstyle sy = (n+g+\delta)k \,. La razón de la convergencia es que y es igual a \scriptstyle f(k), la función del producto per cápita tiene rendimientos decrecientes, así también, la función de inversión efectiva sy\,. De esta forma, los rendimientos decrecientes del capital per cápita hacen que haya una convergencia entre la inversión de reposición y la inversión efectiva. En el gráfico, k "EST" representa el estado de capital estacionario y, por lo tanto, el estado de producto estacionario.

Aumentos en la tasa de ahorro

Un aumento en la tasa de ahorro haría que sy\, aumente, por lo que aumenta el capital de estado estacionario. El efecto de la tasa de ahorro tiene un efecto de crecimiento más rápido en el corto plazo, pero en el largo plazo el efecto es nulo. Básicamente, la tasa de ahorro tiene efectos en el nivel de producto, no así los efectos de la tasa del aumento de la tecnología, que son efectos de crecimientos en el largo plazo.

Condiciones del producto en estado estacionario

Teniendo la igualdad sy = (n+g+\delta)k \,, podemos reemplazar el capital, obteniendo así el capital de estado estacionario.
\frac{K^*}{L}=A\left(\frac{s}{\delta+g+n}\right)^\frac{1}{1-\alpha}.
Además, utilizando y=k^\alpha\,, obtenemos:
\frac{Y^*}{L}=A\left(\frac{s}{\delta+g+n}\right)^\frac{\alpha}{1-\alpha}.
En estado estacionario, es posible determinar las siguientes conclusiones:
  • Aumentos del nivel de tecnología producirían un mayor producto per cápita estacionario. Así también, mayor fuerza de trabajo incidiría positivamente en el producto estacionario. Inversamente, aumentos de la tasa de crecimiento de la población, y altas depreciaciones, tendrían como resultado bajos productos per cápita efectivos estacionarios.
  • En estado estacionario, dado que \Delta k=0\,, la tasa de crecimiento del producto total es igual a n+g y la tasa de crecimiento del producto per cápita es igual a g. El producto per cápita en estado estacionario crecería solo a la tasa de crecimiento de la tecnología.

La regla de oro

La regla de oro consiste en un capital óptimo que maximiza el consumo per cápita. Si asumimos que la utilidad depende del consumo, el capital de estado estacionario no es sinónimo de maximización, ya que con un capital óptimo se puede hacer el consumo máximo. Al respecto, es visible que:
\begin{align} & s\dot{y}=k(n+g+\delta ) \\ & c=y-sy;sy=k(n+g+\delta ) \\ & c=f(k)-k(n+g+\delta ) \\ \end{align}
Esta última ecuación representa el consumo en estado estacionario, es decir, el en el largo plazo. Necesariamente, para encontrar un capital que maximice el consumo, debemos derivar esta ecuación con respecto al capital.
c=f(k)-k(n+g+\delta )
Derivando el consumo respecto al capital, se tiene:
\frac{dc}{dk}=\frac{df(k)}{dk}-(n+g+\delta )
Igualando a cero, se tiene:
\frac{df(k)}{dk}=(n+g+\delta )= {\rm p.m.c.}(k)
Esto nos dice, que el producto marginal del capital, o la última unidad de capital generada debe ser igual a la tasa de crecimiento de la población, la tasa de depreciación y de tecnología para que el consumo sea máximo. Desde el punto de vista algebraico, se tiene que el capital de la regla de oro es el siguiente:
\begin{align} & \alpha k^{\alpha -1}=(n+g+\delta ) \\ & k^{\alpha -1}=\frac{(n+g+\delta )}{\alpha } \\ & k^{1-\alpha }=\frac{\alpha }{n+g+\delta } \\ & k_{RO}=\left( \frac{\alpha }{n+g+\delta } \right)^{\frac{1}{1-\alpha }} \\ \end{align}
Nótese la similitud con el capital estacionario. Se puede inferir, que la tasa de ahorro que maximiza el consumo es la siguiente:
\begin{align} & k_{RO}=k_{EST}=\left( \frac{\alpha }{n+g+\delta } \right)^{\frac{1}{1-\alpha }}=\left( \frac{s}{n+g+\delta } \right)^{\frac{1}{1-\alpha }} \\ & s=\alpha \\ \end{align}
Por lo tanto, necesariamente la condición para que el capital estacionario sea igual al capital de la regla de oro y se maximice el consumo es que la tasa de ahorro debe ser igual a la fracción del producto producida por el capital, es decir \scriptstyle \alpha.

Evidencia empírica

Mankiw, Romer y Weil (1992) basándose en el modelo de Solow examinaron las diferencias internacionales de renta per cápita suponiendo que éstas son una función de la tasa de ahorro, la tasa de crecimiento de la población y los niveles iniciales de productividad del trabajo. Bajo esos supuestos el 60% de las diferencias de renta en 1985 en una muestra de noventa y ocho países parecían ser explicables. Sin embargo, cuando calcularon la contribución implícita del capital en la renta nacional a partir del modelo, resultaron ser casi el doble que las estimaciones directas. Esto suponía una dificultad al modelo de Solow como modelo explicativo.2
Para resolver esta discrepancia construyeron un modelo modificado, que contemplara la acumulación de capital humano. Con ese nuevo modelo podían explicar alrededor del 80% de la variación observada, y una contribución del capital físico cercana al 30% en acuerdo con la cantidad estimada directa. Así que concluyeron que si bien el modelo de Solow no explicaba suficientemente bien los datos una modificación del mismo sí parecía dar cuenta de los datos. Sin embargo, Grossman y Helpman (1994) observan que la productividad total de los factores (PTF) tiene un papel importante. Dado que los incrementos de PTF estimulan la inversión pudiera ser que desde un punto de vista causal no sea la acumulación de capital la causa original del crecimiento sino otros factores que hacen aumentar la PTF.

Uno de los modelos más conocidos de la escuela neoclásicaacerca de la relación entre ahorro, acumulación de capital y crecimiento es el que Robert M. Solow desarrolló a fines de los años cincuenta y sesenta. Este modelo señaló cómo el ahorro, el crecimiento demográfico y el avance tecnológico influían sobre el aumento del producto a lo largo del tiempo.
En 1987, Solow obtuvo el premio Nobel de Economía por su trabajo sobre el crecimiento económico. El modelo fue presentado en: Solow, R. M., "A Contribution to the Theory of Economic Growth". En: Quarterly Journal of Economics, febrero de 1956.
Partía de tres supuestos:
1- La población y la fuerza de trabajo (que se suponen iguales) crecen a una tasa proporcional constante (n) determinada por factores biológicos, pero independiente de otras variables y aspectos económicos.
2- El ahorro y la inversión son una proporción fija del producto neto en un momento dado.
3- La tecnología se supone afectada por dos coeficientes constantes: la fuerza de trabajo por unidad de producto y el capital por producto.
Para comenzar con el análisis, examinemos cómo la oferta y la demanda de bienes determinan la acumulación de capital. La oferta de bienes determina el nivel del producto en un momento dado, y la demanda determina cómo dicho producto se distribuye entre usos alternativos. En el modelo de Solow, la oferta de bienes se basa en la conocida función de producción:
y = F (K, L)
Donde

K = stock de capital
L = trabajo
El modelo de crecimiento de Solow supone que la función de producción tiene rendimientos constantes a escala: al aumentar los insumos trabajo y capital en una determinada proporción, el producto se incrementa en la misma proporción.
La función de producción muestra la productividad marginal decreciente del capital: cada incremento del capital en una unidad causa en la producción un aumento menor que el derivado de la unidad de capital anterior. Esto significa que cuando se dispone sólo de un pequeño capital, una unidad adicional de capital es muy útil y añade una gran cantidad de producción; cuando el capital es muy grande, en cambio, una unidad adicional es menos útil y acrecienta sólo un poco la producción.
Veamos el gráfico de esta función en términos per cápita:
Gráfico 1 Función de producción per cápitaPulsar en las flechas para seguir el trazado del gráfico
La función de producción muestra cómo k (el nivel de capital por trabajador) determina y (el nivel de producción por trabajador):
y = f (k)
La pendiente de la función de producción es la productividad marginal del capital (PMK): si k aumenta en una unidad, y aumenta enPMK unidades. La curva de la función de producción se hace más plana a medida que k aumenta, lo cual indica una productividad marginal decreciente. Dado que la inversión, como se estableció en los supuestos, es igual al ahorro, la tasa de ahorro es también la porción del producto dedicada a la inversión:
Seguimos el planteo original de Solow, que funciona en una economía cerrada al resto del mundo.
S = I
Para un stock de capital K, suponemos que su depreciación es una proporción fija de K, que llamaremos dK. El cambio en el stock de capital es igual a la inversión, neta de depreciación (es decir, la inversión menos esa depreciación):
ΔK = I - dK
Como I = S, y además suponemos que el ahorro es una proporción del producto nacional, S = sY, reemplazamos en la ecuación anterior:
ΔK = sY - dK
Para obtener el cambio en el stock de capital en términos per cápita dividimos la expresión anterior por el tamaño de la fuerza laboral (L):
ΔK / L = sy - dk      (1)
Como la población y la fuerza laboral crecen a una tasa proporcional constante igual a n (por ahora consideraremos nulo el cambio tecnológico), entonces ΔL / L = n.
A su vez, si k = K / L, la tasa de crecimiento de k está dada por la siguiente ecuación:
Δk / k = ΔK / K - ΔL / L = ΔK / K-n
Haciendo un pasaje de términos, ΔK = (Δk / k) K + nK. Si dividimos ambos miembros de la ecuación por L:
ΔK / L = Δk + nk     (2)
Igualando (1) y (2) llegamos a la ecuación fundamental de acumulación de capital:
Δk = sy - (n + d) k
El crecimiento del capital por trabajador Δk (también llamadocoeficiente capital/trabajo) es igual a la tasa de ahorro per cápita(sy) menos el término (n + d) k.
Explicará el alcance de esta ecuación. Como indica el último término, dado que la fuerza laboral crece a una tasa n, un cierto monto del ahorro per cápita debe usarse para equipar a los nuevos participantes de la fuerza laboral con un capital k por trabajador. Para ello se debe aplicar un monto nk de ahorro. Al mismo tiempo, un cierto monto del ahorro per cápita se debe utilizar para reponer el capital depreciado, que es igual a una cantidad dk del ahorro. Por lo tanto, un total (n + d) k del ahorro per cápita se debe usar sólo para mantener constante el coeficiente capital/ trabajo al nivel k. Si el ahorro per cápita es mayor que el monto de (n + d) k, se produce un incremento en el coeficiente capital/ trabajo (Δk > 0).
"Profundización"significa, en este caso, incremento de capital por trabajador (Δk).
El ahorro destinado a equipar a los nuevos participantes de la fuerza laboral y reponer el capital depreciado se denomina ampliación del capital. Por otro lado, el ahorro que se utiliza para hacer subir el coeficiente capital/producto se llama profundización del capital. Por lo tanto, la ecuación fundamental del modelo de Solow establece que:
Profundización de capital = ahorro per cápita menos ampliación del capital
Supongamos que la economía se mantiene en su estado estacionario, es decir, en un equilibrio a largo plazo. En tal caso, el capital por trabajador alcanza un valor de equilibrio y permanece invariable. En consecuencia, el producto por trabajador también alcanza un estado estacionario (recuerde que se omite el cambio tecnológico). Por lo tanto, en estado estacionario tanto k como yalcanzan un nivel permanente.
Ver: Phelps, Edmund S., "The Golden Rule of Accumulation: A Fable for Growthmen': En: American Ecanomic Review,septiembre de 1961.
Para alcanzar el estado estacionario, el ahorro per cápita (sy) debe ser exactamente igual a laampliación del capital ((n + d) k), de modo que Δk = O.
La regla de oro de la acumulación es:
sy = (n + d) k
Aun cuando el estado estacionario significa un valor constante para k e y, no implica un crecimiento nulo. De hecho, en estado estacionario hay un crecimiento positivo del producto a la tasa n. Veamos un gráfico que refleja esta situación:

Gráfico 2 Función de producción, de ahorro y de ampliación de capitalPulsar en las flechas para seguir el trazado del gráfico
El gráfico representa la función de producción per cápita (y). Recordemos qué trabajamos con la hipótesis de rendimientos constantes a escala: si se aumentan los factores, aumenta el producto en la misma proporción.
Nota que, en este punto, todas las variables agregadas de la economía (trabajo, capital y producto) crecen a una tasa igual a n.
La otra curva es la función de ahorro per cápita (sy), que por ser una proporción de la función de producción tiene su misma forma, aunque se encuentra debajo de ella porque el coeficiente s es menor que 1 (0 < s < 1). La recta es la función de ampliación de capital ((n + d) k), cuya pendiente es (n + d).
Como se dijo anteriormente, en estado estacionario se cumple que sy = (n + d) k. En este punto, marcado en el gráfico como A, el capital por trabajador es kA, el producto per cápita es YA, y el ahorro es suficiente para cumplir con la ampliación de capital, lo que significa que el ahorro por persona (syA) alcanza para proporcionar capital a la población en aumento y para reponer el capital depreciado sin causar cambios en el coeficiente de capital por trabajador.
Gráfico 3 Modelo de Solow: estado estacionarioPulsar en las flechas para seguir el trazado del gráfico
A la izquierda del punto A, el ahorro es mayor que el necesario para la ampliación del capital: sy > (n + d) k. Con el aumento en el stock de capital por trabajador se profundiza el capital: k se desplaza hacia la derecha, como lo muestran las flechas. A la derecha de este punto sucede exactamente lo contrario.
Cada vez que la economía se aleja del estado estacionario, ya sea por exceso o por deficiencia de capital por trabajador, hay fuerzas que la empujan hacia el equilibrio de largo plazo del estado estacionario.
Analicemos qué pasa si, a partir de una situación de estado estacionario, modificamos las fuentes de crecimiento, a saber: lapoblación, el capital y la tecnología.

1- Variación en la tasa de crecimiento de la población: si en una economía como la que analiza este modelo crece el número de habitantes (y la fuerza laboral, según los supuestos), una mayor parte del ahorro deberá utilizarse para poder mantener a los nuevos trabajadores con las mismas dotaciones de capital que ya tengan los anteriores. Esta ampliación de capital es igual a nk, lo cual rompe la regia de oro. La curva de ampliación de capital tendrá una pendiente mayor ((n 1 + d) k en el gráfico), que conducirá a un nivel de equilibrio de estado estacionario con un menor ingreso per cápita. Si se produce una disminución en la tasa de población, por el contrario, aumenta el ingreso per cápita. Por esta razón, según este modelo, los países pobres con alto nivel de natalidad poseen un bajo PBN per cápita, lo que equivale a decir que carecen del capital suficiente para toda su fuerza laboral.
Gráfico 4 Variación en la tasa de crecimiento poblacional (n 1)Pulsar en las flechas para seguir el trazado del gráfico
2- Variación en el nivel del capital: Cuando hay un incremento en la tasa de ahorro se verifica una alta tasa de crecimiento, pero sólo hasta llegar al estado estacionario. La variación de la tasa de ahorro puede incidir en 1) la tasa de crecimiento en el corto plazo, y 2) el nivel de ingreso per cápita en el estado estacionario de largo plazo. Cuando se produce una variación positiva del ahorro, la curva sy se traslada as'y como lo indica el siguiente gráfico, lo cual resulta en un incremento transitorio en la tasa de crecimiento, por un lado, y en un incremento permanente en el nivel de ingreso per cápita yen el coeficiente capital! trabajo, por el otro.
Gráfico 5 Variación en la tasa de ahorroPulsar en las flechas para seguir el trazado del gráfico
3- Variación de la tecnología: el cambio tecnológico incrementa la calidad del trabajo y el rendimiento de los trabajadores mediante la especialización, la educación y otros factores. El progreso tecnológico permite un crecimiento sostenido de la producción por trabajador porque desplaza la función de producción. la cual a su vez modifica la función de ahorro. Una vez que la economía se encuentra en estado estacionario, la tasa de crecimiento de la producción por trabajador depende sólo de la tasa de progreso tecnológico. Así, el modelo de Solow demuestra que el progreso tecnológico es la única explicación del constante aumento del nivel de vida.
En el modelo de Solow, la tasa de cambio tecnológico determina latasa de crecimiento de estado estacionario del ingreso per cápita, esto es, el crecimiento del producto por persona.
La conclusión del modelo es: sólo un bajo crecimiento de la población y un cambio tecnológico acelerado pueden generar un aumento permanente en la tasa de crecimiento. Incrementar el ahorro y la inversión, por otra parte, puede producir un incremento transitorio en el crecimiento y uno permanente en el ingreso per cápita. A este modelo, sin embargo, se le puede criticar que intenta mostrar como ejemplo los países industrializados y que olvida incluir el rol de las expectativas.
Mi propósito -escribía Solow en la obra antes citada- era examinar lo que se podría considerar el enfoque más rígido del crecimiento económico y ver si supuestos más flexibles con respecto a la producción permitirían construir un modelo más simple. Desempleo y exceso de capacidad o sus contrarios pueden ser todavía atribuidos a cualquiera de las antiguas causas de déficit o exceso de la demanda agregada, pero menos fácilmente a una desviación de las estrictas condiciones de equilibrio.
En este juicio se percibe una idea subyacente: la economía tiende al crecimiento equilibrado y no a las tensiones y distorsiones expuestas por Harrod.
Finalmente, es importante notar las diferencias entre Solow y Keynescon respecto al crecimiento de la población: mientras que para Keynes el efecto era positivo, porque actuaba sobre la demanda, para Solow era negativo. porque alteraba la relación capital/trabajo.
Publicado por en

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)