Epónimos relacionados con la economía
modelo de Bertrand-Edgeworth de fijación de precios en el oligopolio analiza lo que ocurre cuando hay un producto homogéneo (es decir, los consumidores quieren comprar al vendedor más barato) donde hay un límite a la producción de las empresas que son capaces y/o está dispuesto a vender a un precio determinado. Esto difiere del modelo de competencia a la Bertranddonde se supone que las empresas están dispuestas y son capaces de satisfacer toda la demanda. El límite de salida puede ser considerado como una limitación de capacidad física que es el mismo en todos los precios (como en Edgeworth trabajo 's), o que varían con el precio bajo otros supuestos.
Joseph Louis François Bertrand (1822-1900) desarrolló el modelo de competencia de Bertrand. Este enfoque se basa en la suposición de que hay al menos dos empresas que producen un producto homogéneo con una constante (cero) costo marginal . Los consumidores compran al vendedor más barato. El equilibrio de Nash de este modelo es que todas las empresas (o por lo menos dos) fijan el precio igual al costo marginal (cero). El argumento es simple: si una empresa fija un precio por encima del costo marginal entonces luego otra empresa puede socavarla por una pequeña diferencia en el precio (a menudo llamada épsilon subvaloración, donde épsilon representa una cantidad arbitrariamente pequeña) para que el equilibrio es cero (esto a veces se llama el paradoja de Bertrand).
El enfoque Bertrand asume que las empresas están dispuestas y son capaces de suministrar toda la demanda: no hay límite a la cantidad que se puede producir o vender. Francis Ysidro Edgeworth considera el caso en el que hay un límite a lo que las empresas pueden vender (una restricción de la capacidad): demostró que si hay un límite para lo que las empresas pueden vender, entonces es posible que no exista equilibrio de Nash en estrategias puras (esto a veces se llama la paradoja de Edgeworth)1
Martin Shubik2 desarrolló el modelo de Bertrand-Edgeworth para permitir a la empresa a estar dispuesta a suministrar sólo hasta que su producción de la maximización de beneficios al precio que estableció (en la maximización del beneficio que esto ocurre cuando el costo marginal es igual al precio). A su juicio, en el caso de los costos estrictamente convexos, donde el costo marginal está aumentando conforme aumenta la producción. Shubik demostró que si existe un equilibrio de Nash, que debe ser el precio de competencia perfecta(donde la demanda es igual a la oferta, y todas las empresas fijan precio igual al coste marginal). Sin embargo, esto sólo puede suceder si la demanda del mercado es infinitamente elástica (horizontal) en el precio competitivo. En general, como en la paredoja de Edgeworth, no existirá equilibrio de Nash en estrategias puras. Huw Dixon3 mostró que, en general, un equilibrio de Nash en estrategias mixta existirá cuando hay costos convexos. La prueba de Dixon utiliza el teorema de la existencia de Partha Dasgupta y Eric Maskin.
El Modelo de crecimiento de Ramsey es un modelo de crecimiento económico creado por Frank P. Ramsey (1928) y perfeccionado por David Cass (1965) y Tjalling Koopmans (1965). El modelo de Ramsey se diferencia delmodelo de Solow en que explícitamente modela la opción de consumo en un punto en el tiempo, por lo que la tasa de ahorro es endógena. Como resultado, a diferencia del modelo de Solow, la tasa de ahorro no puede ser constante a lo largo de la transición hacía el estado estacionario. Otra implicación del modelo es que el resultado es óptimo de Pareto, ya que corresponde a la Regla de oro de la tasa de ahorro. Este resultado se debe no sólo a la endogeneidad de la tasa de ahorro, sino también debido a la naturaleza infinita del horizonte de planificación de los agentes en el modelo; no se sostiene en otros modelos endógenos con tasas de ahorro, pero con dinámicas intergeneracionales más complejas, como por ejemplo, los modelos de generaciones solapadas de Samuelson o Diamond.
Originalmente Ramsey establece el modelo como un problema de un planificador central en la maximización de los niveles de consumo a lo largo de sucesivas generaciones. Sólo más tarde fue un modelo adoptado por los investigadores posteriores como una descripción de una economía dinámica y descentralizada.
Gráfica del modelo de crecimiento de Ramsey. La línea azul representa la trayectoria del ajuste dinámico de la economía. Es una ruta estable del sistema dinámico. Las líneas rojas representan trayectorias dinámicas que se rigen por la condición de transversalidad.
Ecuaciones fundamentales del modelo de Ramsey
Hay dos ecuaciones fundamentales del modelo de Ramsey. La primera es la ley del movimiento de la acumulación de capital:
donde k es el capital por trabajador, c es el consumo por trabajador, f (k) es la producción por trabajador, 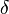 es la tasa de depreciación del capital. Esta ecuación simplemente dice que la inversión o el incremento del capital por trabajador es la parte de la producción que no se consume, menos la tasa de depreciación del capital.
es la tasa de depreciación del capital. Esta ecuación simplemente dice que la inversión o el incremento del capital por trabajador es la parte de la producción que no se consume, menos la tasa de depreciación del capital.
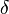 es la tasa de depreciación del capital. Esta ecuación simplemente dice que la inversión o el incremento del capital por trabajador es la parte de la producción que no se consume, menos la tasa de depreciación del capital.
es la tasa de depreciación del capital. Esta ecuación simplemente dice que la inversión o el incremento del capital por trabajador es la parte de la producción que no se consume, menos la tasa de depreciación del capital.
La segunda ecuación se refiere a la conducta de ahorro de los hogares y es menos intuitiva. Si los hogares están maximizando su consumo intertemporalmente, en cada punto en el tiempo equiparan el beneficio marginal del consumo presente con el de consumo en el futuro, o equivalentemente, el beneficio marginal del consumo en el futuro con su costo marginal. Debido a que este es un problema intertemporal, esto significa una igualación de las tasas en lugar de los niveles. Hay dos razones por las cuales las familias prefieren consumir ahora y no en el futuro. En primer lugar, ellos descuentan el consumo a futuro. En segundo lugar, porque la función de utilidad es cóncava, los hogares prefieren alisar su consumo (es decir, consumir “más o menos la misma cantidad cada día). Un aumento o una ruta de descenso del consumo reduce la utilidad del consumo en el futuro. Por lo tanto la siguiente relación caracteriza la relación óptima entre las diferentes tasas: tasa de retorno sobre los ahorros = velocidad a la que el consumo se descuenta – cambio porcentual en la utilidad marginal más el crecimiento del consumo.
Matemáticamente:
Una clase de funciones de utilidad que sean compatibles con un estado de equilibrio de este modelo son las funciones de utilidad de la forma:
En este caso tenemos:
que es una constante. Entonces la solución de la ecuación dinámica anterior para el crecimiento del consumo se obtiene:
que es la segunda ecuación dinámica clave del modelo y se suele llamar la "ecuación de Euler".
Con una función de producción neoclásica con rendimientos constantes a escala, la tasa de interés, r, será igual al producto marginal del capital por trabajador. Un caso particular está dada por la función de producción Cobb-Douglas
lo que implica que la tasa de interés bruto
por lo tanto el tipo de interés neto r
Ajustando
 y
y  igual a cero, podemos encontrar el estado estacionario de este modelo.
igual a cero, podemos encontrar el estado estacionario de este modelo.Las empresas y los consumidores en el modelo
Como sabemos, las empresas contratan por un precio "r", que es el precio de arrendamiento del capital. Este estará dado por el producto marginal, por lo tanto:

Que evidentemente es:

Además, por el lado del sector empleado, el salario real estará dado por:

Que representa todo el ingreso de la economía , menos la parte que ingresa al capital, por lo tanto lo que se le paga a los trabajadores en términos percápita.
Por último, adoptaremos una tasa de interés R(T) en donde
 dt
dt
Por lo que la tasa de interés R "mayúscula" indica la tasa de interés acumulada durante el periodo de vida de los individuos.
El modelo de Ramsey-Cass-Koopmans o el modelo de crecimiento de Ramsey es un modelo neoclásico de crecimiento económico basado principalmente en el trabajo del economista y matemático Frank P. Ramsey, con extensiones significativas hechas por David Cass y Koopmans Tjalling. El modelo de Ramsey difiere del modelo de Solow ya que modeliza explícitamente la elección de consumo en un punto en el tiempo y así como endogeneiza la tasa de ahorro. Como resultado, al contrario que en el modelo de Solow, la tasa de ahorro puede no ser constante a lo largo de la transición al estado de equilibrio a largo plazo. Otra implicación del modelo es que el resultado es un óptimo de Pareto o Pareto eficiente. Este resultado se debe no sólo a la endogeneidad de la tasa de ahorro, sino también por la naturaleza infinita del horizonte de planificación de los agentes en el modelo, sino que no se sostiene en otros modelos con tasas de ahorro endógenas sino dinámicas intergeneracionales más complejas, por ejemplo, modelos generaciones superpuestas de Samuelson o Diamond.
Originalmente Ramsey establece el modelo como el problema de un planificador central de maximizar los niveles de consumo a lo largo de sucesivas generaciones. Sólo más tarde fue un modelo adoptado por los investigadores posteriores como una descripción de una economía dinámica y descentralizada.

Gráfico de espacio de fase (o diagrama de fases) del modelo de Ramsey. La línea azul representa el ajuste dinámico (o silla) Ruta de la economía en la que todas las limitaciones presentes en el modelo están satisfechos. Es un camino estable del sistema dinámico. Las líneas rojas representan trayectorias dinámicas que se rigen por la condición de transversalidad.
Ecuaciones fundamentales del modelo de Ramsey
Hay dos ecuaciones fundamentales del modelo de Ramsey. La primera es la ley del movimiento de acumulación de capital:
Originalmente Ramsey establece el modelo como el problema de un planificador central de maximizar los niveles de consumo a lo largo de sucesivas generaciones. Sólo más tarde fue un modelo adoptado por los investigadores posteriores como una descripción de una economía dinámica y descentralizada.

Gráfico de espacio de fase (o diagrama de fases) del modelo de Ramsey. La línea azul representa el ajuste dinámico (o silla) Ruta de la economía en la que todas las limitaciones presentes en el modelo están satisfechos. Es un camino estable del sistema dinámico. Las líneas rojas representan trayectorias dinámicas que se rigen por la condición de transversalidad.
Ecuaciones fundamentales del modelo de Ramsey
Hay dos ecuaciones fundamentales del modelo de Ramsey. La primera es la ley del movimiento de acumulación de capital:
donde k es el capital por trabajador,
 es el cambio en el capital por trabajador en el tiempo, c es el consumo por trabajador, f (k) es la producción por trabajador, y
es el cambio en el capital por trabajador en el tiempo, c es el consumo por trabajador, f (k) es la producción por trabajador, y  es la tasa de depreciación del capital. Esta ecuación simplemente establece que la inversión, o el aumento de capital por trabajador es la parte de la producción que no se consume, menos la tasa de depreciación del capital. La inversión es, por lo tanto, el mismo que ahorro.
es la tasa de depreciación del capital. Esta ecuación simplemente establece que la inversión, o el aumento de capital por trabajador es la parte de la producción que no se consume, menos la tasa de depreciación del capital. La inversión es, por lo tanto, el mismo que ahorro.donde I es el nivel de inversión, Y es el nivel de ingresos y s es la tasa de ahorro, o la proporción de los ingresos que se ahorra.
La segunda ecuación se refiere al comportamiento del ahorro de los hogares y es menos intuitiva. Si los hogares maximizan su consumo intertemporal, en cada punto en el tiempo que igualan el beneficio marginal del consumo actual con el de consumo en el futuro, o lo que es equivalente, el beneficio marginal del consumo en el futuro con su costo marginal. Debido a que este es un problema intertemporal esto significa una igualación de las tasas en lugar de los niveles. Hay dos razones por las que las familias prefieren consumir ahora y no en el futuro. En primer lugar, descontar el consumo futuro. En segundo lugar, debido a que la función de utilidad es cóncava, las familias prefieren una trayectoria de consumo suave. Un aumento o disminución de una trayectoria de consumo reduce la utilidad del consumo en el futuro. Por lo tanto la siguiente relación caracteriza a la relación óptima entre los diversos tipos de:
tasa de rendimiento del ahorro = velocidad a la que se descuenta el consumo - porcentaje de cambio en tiempos de utilidad marginal del crecimiento del consumo.
Matemáticamente:
 ,
,
Una clase de funciones de utilidad que son compatibles con un estado constante de este modelo son las funciones de utilidad isoelástica o funciones de aversión relativa al riesgo constante (CRRA), dada por:
 ,
,
En este caso tenemos:

A continuación, la solución de la ecuación dinámica por encima del crecimiento del consumo se obtiene:
 ,
,
que es la segunda ecuación dinámica fundamental del modelo y por lo general se llama la "ecuación de Euler".
Con una función de producción neoclásica con rendimientos constantes a escala, la tasa de interés, r, será igual al producto marginal del capital por trabajador. Un caso particular es dada por la función de producción Cobb-Douglas
Con una función de producción neoclásica con rendimientos constantes a escala, la tasa de interés, r, será igual al producto marginal del capital por trabajador. Un caso particular es dada por la función de producción Cobb-Douglas
 ,
,
lo que implica que la tasa de interés bruto es
 ,
,
por lo tanto, la tasa de interés neta r
 ,
,
Fijando a  y
y  igual a cero se encuentra el estado de equilibrio de este modelo.
igual a cero se encuentra el estado de equilibrio de este modelo.
 y
y  igual a cero se encuentra el estado de equilibrio de este modelo.
igual a cero se encuentra el estado de equilibrio de este modelo.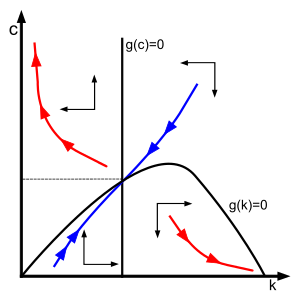










No hay comentarios:
Publicar un comentario