Epónimos relacionados con la economía
La curva de Laffer representa la relación existente entre los ingresos fiscales y los tipos impositivos, muestra cómo varía la recaudación fiscal al modificar los tipos impositivos. Fue difundida por el economista Arthur Laffer, aunque cinco siglos antes el estudioso andalusí Ibn Jaldún ya había teorizado sobre la relación entre los tipos impositivos y la recaudación, y también John Maynard Keynes unos pocos años antes.

La curva muestra en abscisas los tipos impositivos posibles (t) y en ordenadas la recaudación fiscal (T) que se consigue a ese tipo impositivo. El máximo aparece en el centro por cuestiones de claridad, en una curva real podría estar desplazado a la derecha o a la izquierda. Aunque más posiblemente a la derecha.
Explicación
Al representar los ingresos fiscales en relación con el tipo impositivo, si el tipo impositivo es cero, los ingresos fiscales serán también nulos. Si, por el contrario, los tipos impositivos son del 100%, los ingresos fiscales también se anularán, nadie ofrecería ni demandaría el bien en cuestión. Según Laffer, entre estos dos puntos extremos, los ingresos en función del tipo primero aumentarán para a continuación disminuir hasta llegar a cero. El fundamento matemático es el teorema de Rolle, en virtud del cual si el ingreso fiscal es una función continua del tipo impositivo, entonces tiene (al menos) un máximo (ya que se trata de una función siempre positiva) en un punto intermedio del intervalo, pero no necesariamente en el centro.
La curva de Laffer muestra que el incremento de los tipos impositivos no siempre conlleva un aumento de la recaudación fiscal. La característica más importante de esta curva reside en que indica que cuando el tipo impositivo es suficientemente alto (t* en la gráfica adjunta), si se sube aún más, los ingresos recaudados pueden terminar disminuyendo. La disminución de la oferta del bien reduce hasta tal punto los ingresos fiscales que la subida del tipo impositivo no compensa la disminución de la oferta. Este fenómeno se denomina efecto Laffer, en honor al economista Arthur Laffer que hizo este gráfico a principios de la década de 1980.
La curva de Laffer y la política fiscal de Reagan
Cuando Ronald Reagan se presentó a la presidencia de Estados Unidos en 1980, incluyó la reducción de impuestos en su programa. Sostenía que los impuestos eran tan altos que disuadían de trabajar a muchos ciudadanos y que una reducción de los tipos impositivos daría a los individuos incentivos suficientes para trabajar, lo que provocaría la mejora del bienestar económico y quizás incluso de los ingresos fiscales. Esta política económica se conoció como «economía de la oferta» puesto que trataba de incrementar la oferta de trabajo.
Los hechos no confirmaron la conjetura de Laffer de que una reducción de los tipos impositivos elevaría los ingresos fiscales. Cuando Reagan bajó los impuestos al ser elegido presidente de los Estados Unidos, el resultado fue una reducción de los ingresos fiscales. El impuesto sobre la renta disminuyó un nueve por ciento entre 1980 y 1984, aun cuando la renta media creció un cuatro por ciento. Históricamente se inició un periodo de fuerte déficits fiscales.2 Parece bastante improbable en el caso de los tipos impositivos existentes en Estados Unidos que se haya producido el efecto Laffer. Sin embargo, en otros países, como Suecia, en que son mucho más altos, existen algunas pruebas de que puede haberse producido el fenómeno de la curva de Laffer.1
Opiniones de otros economistas
Según Paul Samuelson los ingresos fiscales disminuyeron considerablemente en relación con la tendencia observada tras las reducciones de los impuestos en la era Reagan.3
John Kenneth Galbraith ha criticado duramente la curva de Laffer:
«Partiendo de la circunstancia indiscutible de que si no se imponían gravámenes no se recogería ningún ingreso público y de que si los impuestos absorbían todos los recursos no se produciría ninguna renta, el profesor Laffer unió estas dos verdades indiscutibles con una curva a mano alzada que mostraba que, aumentando los tipos impositivos, el total de los recursos públicos primero aumentaría y luego caería. (...) En un ejercicio posterior de imaginación, el profesor Laffer pasó a sostener que la presión fiscal había superado en Estados Unidos el punto óptimo, obtenido, como ya dijimos, a mano alzada. (...) Es evidente que nadie en su sano juicio se tomó en serio la curva y las conclusiones del profesor Laffer. Hay que otorgarle, sin embargo, el mérito de haber demostrado que una manipulación justificativa, aunque evidente, podía ser de gran utilidad práctica. La reducción impositiva de la década de los ochenta fue, en no escasa medida, producto de la invención de Laffer.»4
Por su parte Milton Friedman afirmó que «If a tax cut increases government revenues, you haven't cut taxes enough» (Si una reducción de impuestos aumenta los ingresos del gobierno, es que no se han reducido los impuestos lo suficiente).
La curva de Laffer es una representación gráfica de como afecta la variación del tipo impositivo (10%, 20%, 30%,...) en la cantidad total de recaudación fiscal de un impuesto.
Pese a que una primera aproximación haría pensar que a mayor tipo impositivo debería llevarnos a una mayor recaudación, analizando en detalle cada caso, la realidad en un mundo global, nos lleva a que esto no es así, por ejemplo:
- Una subida excesiva del tipo impositivo
sobre las rentas del trabajo desincentivará a las personas a trabajar más y conseguir mejores sueldos.
- Igual al caso anterior es el caso de Sociedades mercantiles, un mayor tipo impositivo puede suponer un desincentivo a su actividad.
- Una subida de las rentas del capital incentivará a que las personas con elevados patrimonios se trasladen a otro país donde estas rentas tengan una tributación menor.
- Una subida del Impuesto sobre el consumo (IVA) puede reducir el consumo e incluso en aquellos casos que le sea posible consumirá en otros países con menor tributación.
- Además de todo lo anterior una subida de impuestos incentivará la economía sumergida y el fraude.
Igualmente, una menor tributación puede aumentar la recaudación porque:
- Incentivará la actividad, incluso empresas extranjeras podrán plantearse instalarse en ese país. Esta recaudación fiscal no se produciría.
- Atraerá consumo.
- Detraerá parte de la economía sumergida y el fraude.
Si a lo anterior unimos que la recaudación se consigue a través de distintos impuestos, la fijación de las tipos impositivos se convierte en una labor difícil ya que deben cruzarse distintas Curvas de Laffer, por ejemplo:
- Los bajos tipos del Impuesto de Sociedades en Irlanda hicieron que la recaudación por este impuesto fuese baja inicialmente (entre otras cosas por un bajo inver de empresas existentes en el país), pero hizo que distintas empresas implantasen sus oficinas para Europa allí (Microsoft, Google,...) esto hizo que la recaudación global subiese ya que además del Impuesto de Sociedades quee no habrían recaudado con un impuesto más alto (se habrían instalado en otro país), su implantación generó empleo e incluso el traslado de personal de otros países europeos a Irlanda, lo que trajo mayor recaudación vía Impuesto de la Renta e IVA vía el consumo de esas personas.
- También es significativo el efecto de las variaciones en los impuestos sobre las rentas del capital (ganancias por el patrimonio vía inversiones en bolsa, depósitos, inmuebles, ...) de patrimonios elevados. Si el tipo es alto, dada la libertad que existe en el tránsito de personas y capitales, se incentivará que estas personas se trasladen a otro país con menor tributación, motivo que ha atraido a muchos millonarios de Europa a vivir en Mónaco, Suiza o a Hong-Kong o Singapur a los asiáticos. Podría pensarse en un principio que si no van a "pagar" pues que más da que se vayan, pero la realidad es que estas personas al tener un ritmo de vida alto son las que más consumen en proporción y generan una recaudación por IVA muy elevada. Es por eso que los países antes mencionados consiguen una alta recaudación ya que compensan los menores ingresos de las rentas del capital con altas recaudaciones del impuesto sobre consumo (IVA).
La curva de Lorenz es una representación gráfica utilizada frecuentemente para plasmar la distribución relativa de una variable en un dominio determinado. El dominio puede ser el conjunto de hogares o personas de una región o país, por ejemplo. Lavariable cuya distribución se estudia puede ser el ingreso de los hogares o las personas. Utilizando como ejemplo estas variables, la curva se trazaría considerando en el eje horizontal el porcentaje acumulado de personas u hogares del dominio en cuestión y en el eje vertical el porcentaje acumulado del ingreso. Su autoría es de Max O. Lorenz en 1905.
Cada punto de la curva se lee como porcentaje acumulativo de los hogares o las personas. La curva parte del origen (0,0) y termina en el punto (100,100). Si el ingreso estuviera distribuido de manera perfectamente equitativa, la curva coincidiría con la línea de 45 grados que pasa por el origen (por ejemplo el 30% de los hogares o de la población percibe el 30% del ingreso). Si existiera desigualdad perfecta, o sea, si un hogar o persona poseyera todo el ingreso, la curva coincidiría con el eje horizontal hasta el punto (100,0) donde saltaría el punto (100,100). En general la curva se encuentra en una situación intermedia entre estos dos extremos.

Curva de Lorenz y desigualdad
Si una curva de Lorenz se encuentra siempre por encima de otra (y, por lo tanto, está más cerca de la línea de 45 grados que la otra), entonces podemos decir, sin ambigüedad, que la primera exhibe menor desigualdad que la segunda. Esta comparación gráfica entre distribuciones de distintos dominios geográficos o temporales es el principal empleo de las curvas de Lorenz. El indicador gráfico de bienestar más usado es la Curva de Lorenz Generalizada (CLG), que es una derivación de la curva de Lorenz habitual. La CLG sólo se diferencia de la de Lorenz en que en la escala vertical no se representan las cantidades relativas acumuladas sino las cantidades acumuladas (no relativas) divididas por el número N de elementos de la población. La lógica pretendida es representar qué cantidad absoluta corresponde a cada porcentaje de individuos. Para clarificar este aspecto, supóngase que la curva de Lorenz normal de una población nos dice que el 50% de los menos ricos poseen el 25% de la riqueza total. Se puede comprender que es muy diferente la situación de bienestar de este 50% de la población según si la riqueza total es muy pequeña o muy grande. Es obvio que es peor poseer el 50% de una cantidad pequeña que poseer el 25% de una cantidad mucho mayor. El dividir las cantidades acumuladas por el total de elementos N es necesario para poder comparar riquezas entre poblaciones distintas que tengan un número diferente de elementos: no es lo mismo una riqueza total de 1.000.000€ en un conjunto de 10 personas que esa misma riqueza total en un conjunto formado por 1.000 personas.
Ecuación de la curva de Lorenz
Si se conoce la distribución de la renta como densidad de probabilidad  para cada valor de renta, la curva de Lorenz puede encontrarse analíticamente en función de ésta. La proporción de personas o unidades familiares con una renta inferior a un nivel de renta r viene dada por:
para cada valor de renta, la curva de Lorenz puede encontrarse analíticamente en función de ésta. La proporción de personas o unidades familiares con una renta inferior a un nivel de renta r viene dada por:
 para cada valor de renta, la curva de Lorenz puede encontrarse analíticamente en función de ésta. La proporción de personas o unidades familiares con una renta inferior a un nivel de renta r viene dada por:
para cada valor de renta, la curva de Lorenz puede encontrarse analíticamente en función de ésta. La proporción de personas o unidades familiares con una renta inferior a un nivel de renta r viene dada por:(1)
Mientras que la proporción de renta acumulada por las personas con rentas iguales o inferiores a r viene dada por:
(2)
Donde 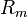 es la renta media. Las ecuaciones () y () constituyen juntas las ecuaciones paramétricas de la curva en función del parámetro r.
es la renta media. Las ecuaciones () y () constituyen juntas las ecuaciones paramétricas de la curva en función del parámetro r.
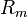 es la renta media. Las ecuaciones () y () constituyen juntas las ecuaciones paramétricas de la curva en función del parámetro r.
es la renta media. Las ecuaciones () y () constituyen juntas las ecuaciones paramétricas de la curva en función del parámetro r.Propiedades
La curva de Lorenz tiene pendiente positiva en todos sus puntos como se deduce de la siguiente relación:
(3)
En el punto inicial  la pendiente será nula (aun en el caso
la pendiente será nula (aun en el caso  el límite anterior sigue siendo válido, pero en el resto de puntos será estrictamente positiva.
el límite anterior sigue siendo válido, pero en el resto de puntos será estrictamente positiva.
 la pendiente será nula (aun en el caso
la pendiente será nula (aun en el caso  el límite anterior sigue siendo válido, pero en el resto de puntos será estrictamente positiva.
el límite anterior sigue siendo válido, pero en el resto de puntos será estrictamente positiva.
Además la curva de Lorenz es convexa ya que su derivada segunda siempre es positiva:
(4)
Ejemplo 1
En esta sección calculamos la curva de Lorenz y el índice de Gini para una distribución de renta exponencial. Aunque ésta no parece una distribución adecuada para la renta nacional de ningún país, la sencillez de las expresiones obtenidas permite entender de modo sencillo la aplicación de las ecuaciones () a (). Para un país con una renta nacional media  con una distribución exponencial la densidad de probabilidad de la distribución será:
con una distribución exponencial la densidad de probabilidad de la distribución será:
 con una distribución exponencial la densidad de probabilidad de la distribución será:
con una distribución exponencial la densidad de probabilidad de la distribución será:
Esta expresión permite calcular la proporción de personas por debajo de una cierta renta y la renta acumulada de ese grupo de personas fácilmente:
Despejando  de la primera ecuación y substituyendo el resultado en la segunda se obtiene la curva de Lorenz explícitamente:
de la primera ecuación y substituyendo el resultado en la segunda se obtiene la curva de Lorenz explícitamente:
 de la primera ecuación y substituyendo el resultado en la segunda se obtiene la curva de Lorenz explícitamente:
de la primera ecuación y substituyendo el resultado en la segunda se obtiene la curva de Lorenz explícitamente:
El índice de Gini se puede calcular simplemente como:
Este es el valor exacto. Cuando para calcular este valor en lugar de una distribución continua se usa un cálculo aproximado por decilas en cambio resulta sólo  .
.
 .
.Ejemplo 2
Una aproximación más verosimil para la renta nacional es usar en lugar de una simple distribución exponencial, unadistribución gamma:
Donde el parámetro  está relacionado con la renta media mediante
está relacionado con la renta media mediante  . Después de una cierta cantidad de álgebra trivial pero engorrosa puede encontrarse que la proporción de personas por debajo de una cierta renta y la renta acumulada de ese grupo de personas vienen dadas por:
. Después de una cierta cantidad de álgebra trivial pero engorrosa puede encontrarse que la proporción de personas por debajo de una cierta renta y la renta acumulada de ese grupo de personas vienen dadas por:
 está relacionado con la renta media mediante
está relacionado con la renta media mediante  . Después de una cierta cantidad de álgebra trivial pero engorrosa puede encontrarse que la proporción de personas por debajo de una cierta renta y la renta acumulada de ese grupo de personas vienen dadas por:
. Después de una cierta cantidad de álgebra trivial pero engorrosa puede encontrarse que la proporción de personas por debajo de una cierta renta y la renta acumulada de ese grupo de personas vienen dadas por:
Donde:
En este caso no es posible despejar explícitamente  de la primera ecuación. Aunque puede calcularse el índice de Gini mediante la expresión (para
de la primera ecuación. Aunque puede calcularse el índice de Gini mediante la expresión (para  entero):
entero):
 de la primera ecuación. Aunque puede calcularse el índice de Gini mediante la expresión (para
de la primera ecuación. Aunque puede calcularse el índice de Gini mediante la expresión (para  entero):
entero):
En este caso el coeficiente de Gini tampoco depende de la renta media. Dado que el índice de Gini de la mayor parte de países está entre 0,50 y 0,25 la distribución gamma anterior puede usarse de manera aproximada para reproducir la distribución real de la renta.
La curva de Lorenz es una representación gráfica de la desigualdad en el reparto de la renta existente en un determinado territorio (normalmente un país). En ella, se sitúa en el eje X los acumulados de población (P) expresados en tanto por ciento y en el eje Y los acumulados de renta (Q) expresados en tanto por ciento.
Por lo tanto, en el punto (0;0) encontramos siempre que el 0% de la población dispone del 0% de la renta y en el punto (1;1) que el 100% de la población dispone del 100% de la renta, como es lógico.
Entendido esto, podemos comprender que cuánto más cerca esté la curva de la recta que une el (0;0) con el (1;1), (línea roja), mejor estará distribuida la renta, siendo la citada recta la distribución más igualitaria posible, en la que todos los ciudadanos de una población dispondrían exactamente de los mismos ingresos. De la misma forma, cuanto mayor sea el área que queda entre la citada recta y la curva, mayor será la desigualdad existente, la población representada por la línea azul tiene una distribución más igualitaria que la representada por la línea verde).
En la gráfica mostrada en la parte superior del artículo estaríamos comparando la curva de Lorenz de 2 territorios y se llegaría a las siguientes conclusiones: en la curva verde al observar el punto 3 concluiríamos que el 60% de la población posee el 20% de la renta, y en la curva azul al observar el punto 2, llegaríamos a la conclusión de que en ese territorio, el 60% de la población posee aproximadamente el 40% de la renta. Adicionalmente, realizando una comparación entenderíamos que el territorio representado por la línea azul tiene una distribución de la renta más igualitaria o equitativa que el representado por la curva verde, dado que como ya he mencionado, cuanto más cerca esté la curva de la recta roja más igualitaria es la distribución de la renta en un territorio.
Todo lo mencionado se puede calcular matemáticamente a través de el índice de Gini, ya que existe una relación entre la Curva de Lorenz y el índice de Gini.

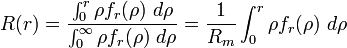






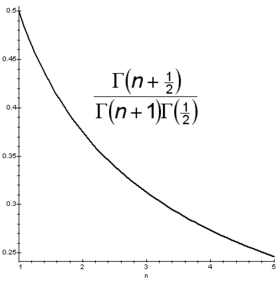
 . El valor de n corresponde a cada distribución, mientras que el factor
. El valor de n corresponde a cada distribución, mientras que el factor 



No hay comentarios:
Publicar un comentario