Diagrama de Schlegel

Ejemplos coloreados por el número de lados de cada cara. Amarillo: triángulos, Rojo: cuadrados y Verde:pentágonos.

Un teseracto proyectado en el espacio tridimensional como diagrama de Schlegel. Existen 8 celdas cúbicas visbles, uno en el centro, uno sobre cada una de las seis caras exteriores del mismo, y un último cubo que representa el "interior" representando el espacio fuera de la frontera cúbica.

En geometría, un diagrama de Schlegel es una proyección de un politopo contenido en

R^d

sobre el espacio

R^{d-1}

a través de un punto que está más allá de una de sus "caras". La entidad resultante es una división politópica de las caras en

R^{d-1}

que es combinatoriamente equivalente al politopo original. En 1886 Victor Schlegel introdujo esta herramiento para estudiar propiedades combinatorias y topológicas de los politopos. En dimensiones, 3 y 4, un diagrama de Schlegel es una proyección de un poliedro sobre el plano dando una figura plana y una proyección de un polícoro al espacio tridimensional, respectivamente. Como tal, los diagramas de Schlegel se usan frecuentemente para visualizar politopos del espacio de cuatro dimensiones.

El diagrama de Schlegel

El diagrama de Schlegel de un poliedro es una representación que lleva las aristas de un poliedro a un diseño en el plano. Es como si un objeto tridimensional se aplanara. Sería el resultado de plasmar en un papel lo que vemos cuando miramos el armazón del poliedro construido con varillas (como los del omnipoliedro). Pero hay que acercarse mucho, de forma que veremos un polígono grande y otros más pequeños en su interior.

El diagrama de Schlegel del cubo es la figura poligonal de la derecha:

Es interesante ver que en este diagrama una cara contiene las imágenes del resto de vértices, aristas y caras aunque sus tamaños y formas se distorsionen.

Dibuja los diagramas de Schlegel de los otros sólidos platónicos y de los sólidos arquimedianos.

esfera consciente de Alexander es una 2-esfera embebida en R³, cuyo exterior no es homeomorfoal exterior de la 2-esfera canónica en R³.

Fue descubierta en 1924 por el matemático James Alexander como un ejemplo patológico que mostraba la imposibilidad de generalizar el Teorema de la curva de Jordan-Schönflies a dimensiones superiores.

Esfera cornuda de Alexander.

Descripción informal

Descrita de modo informal, se construye, como muestra la figura, sacando dos "cuernos" a una esfera, aproximándolos, dividiendo en dos cada uno de los cuernos anteriores y volviéndolos a aproximar, repitiendo el proceso indefinidamente.

Representa un objeto topológicamente equivalente a la 2-esfera canónica de R³, pero embebido en R³ de forma muy diferente. Si nos fijamos en el exterior de la esfera cornuda de Alexander, encontraremos que la esfera se encuentra anudada. En una esfera canónica siempre podremos liberar una cuerda atada en su exterior, pero en la esfera cornuda de Alexander será imposible liberar una cuerda que tenga que pasar a través de los cuernos entrelazados.

Así, del mismo modo que todos los nudos como espacios topológicos son homeomorfos a una circunferencia, pero nudos no equivalentes pueden tener exteriores no homeomorfos, la esfera canónica de R³ y la esfera cornuda de Alexander son homeomorfas y sus exteriores no.

Un poco de historia

En 1909 se completó la demostración del Teorema de la curva de Jordan-Schönflies. Como consecuencia directa del mismo, quedaba demostrado que cualquier curva cerrada simple dividía el plano en dos regiones: la interior, homeomorfa al interior del disco unidad, y la exterior, homeomorfa al exterior del mismo disco.

En 1921, J. W. Alexander buscaba un análogo en dimensión superior de este teorema. Cuando creía tener probado este resultado, descubrió un fallo. En 1924 descubrió como contraejemplo la esfera cornuda: su exterior no era homeomorfo al exterior de la esfera canónica.

Esfera de Riemann

	fig.1: Proyección estereográfica del plano complejo extendido sobre la "esfera de Riemann".

	fig.2: La "esfera de Riemann" puede ser visualizada como el plano complejo envuelto alrededor de una esfera.

En matemática, la esfera de Riemann (o plano complejo extendido), llamada así en honor al matemático del siglo XIX Bernhard Riemann, es una esfera obtenida del plano complejo mediante la adición de un punto del infinito. La esfera es la representación geométrica de los números complejos extendidos, denotado como

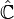\hat\mathbb{C}

\mathbb{C} \cup \{\infty\}

,¹ (véase fig.1y fig.2), la cual consiste en los números complejos ordinarios en conjunción con el símbolo

\infty\!

para representar el infinito.

Los números complejos extendidos son comunes en análisis complejoporque permiten la división por cero en algunas circunstancias, en el sentido de hacer expresiones bien definidas tales como:

1 / 0 = \infty

Por ejemplo, cualquier función racional sobre el plano complejo puede ser extendida como una función continua sobre la esfera de Riemann, con los polos de la función racional mapeados al infinito. Más generalmente, cualquier función meromorfa puede ser pensada como una función continua cuyo codominio es la esfera de Riemann.

En geometría, la esfera de Riemann es el ejemplo prototípico de una superficie de Riemann, y una de las más simples variedades complejas. En geometría proyectiva, la esfera puede ser pensada como la recta proyectiva compleja

\mathbb{CP}^1

, el espacio proyectivo de todos las rectas complejas en

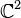\mathbb{C}^2

. Como con cualquier superficie de Riemann compacta, la esfera también puede ser vista como unacurva algebraica proyectiva, haciendo de esto un ejemplo fundamental de geometría algebraica. También encuentra utilidad en otras disciplinas que dependen del análisis y de la geometría, como puede ser la mecánica cuántica y otras ramas de la física.

Esfera de Riemann

El plano complejo es representado por el plano de Argand, pero existe el llamado plano complejo extendido el cual es el plano complejo más el punto que representa el infinito $(C \cup \infty)$ . En topología una esfera es un plano más un punto por lo que podemos deducir que el plano extendido de los números complejos, denotado por

, es representado geométricamente como la superficie de una esfera, llamada Esfera de Riemann en honor a su "creador" o "descubridor". Todos los puntos en la esfera tienen representación en el plano complejo excepto el infinito.