Círculos exinscritos
Sea ABC un triángulo (en verde en la figura). Tracemos sus lados, considerados como rectas (en negro). Las bisectrices interiores y exteriores (en rojo) se intersecan en cuatro puntos: uno es el centro del círculo inscrito (en pardo), y los demás son centros de los círculos exinscritos (en amarillo). Estos últimos están "inscritos" en el sentido de que son tangentes simultáneamente a los tres lados, y se hallan al exterior del triángulo, de ahí su apelación.
La demostración es la misma que en el caso del círculo inscrito. Tomemos por ejemplo la bisectriz interior en A las exteriores en B y C.
La demostración es la misma que en el caso del círculo inscrito. Tomemos por ejemplo la bisectriz interior en A las exteriores en B y C.
- Primero constatamos que no pueden ser paralelas, porque los lados del triángulo no lo son.
- En segundo lugar consideremos la intersección de las dos bisectrices procedentes de B y C. Este punto, A', es por definición equidistante de los lados (AB) y (CB) por una parte, y de (AC) y (BC) por otra, por lo tanto es equidistante de (CA) y (BA), luego pertenece a una bisectriz procediente de A. No puede ser la bisectriz exterior que se halla fuera del sector angular BAC mientras que A' está dentro, por lo tanto es la bisectriz interior.
- El punto A' es equidistante de los tres lados (AB), (AC) y (BC). Sea d esta distancia común. Entonces el círculo de centro A' y de radio d es tangente a los tres lados.
Una curiosidad: las bisectrices interiores son las alturas del triángulo A'B'C', lo que permite hacer el camino inverso y volver a encontrar el triángulo inicial a partir de los tres círculos exinscritos.

Las circunferencias exinscritas de un triángulo son las circunferencias tangentes a un lado y a las prolongaciones de los otros dos. Tienen por centros los excentros.
En geometría, la circunferencia circunscrita es la circunferencia que pasa por todos los vértices de una figura plana y contiene completamente a dicha figura en su interior.1 El centro de la circunferencia circunscrita se llama circuncentro2 3 y su radiocircunradio4 5
Un polígono que tiene una circunferencia circunscrita se llama polígono cíclico.6 Todos los polígonos simples regulares, todos lostriángulos y todos los rectángulos son cíclicos. En todo polígono cíclico, el circuncentro se halla en el punto de intersección de lasmediatrices de los lados del polígono.
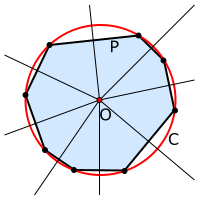
Circunferencia circunscrita de triángulos
El circuncentro (símbolo O) es el punto en el que se intersecan las tres mediatrices de un triángulo y es el centro de la circunferencia circunscrita.7
Los vértices de un triángulo, como extremos de cada lado, se encuentran a la misma distancia de los puntos de sus mediatrices, luego el punto donde estas se cortan, será equidistante de los tres vértices: el circuncentro. Dicho punto se suele expresar con la letra O.
Sirve para trazar el círculo que pasa por los tres vértices del triángulo.
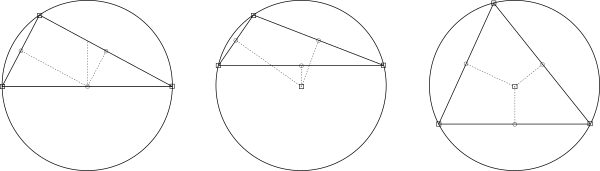
Tres casos de triángulos:
- Triángulo rectángulo, circuncentro en el punto medio de la hipotenusa.
- Triángulo obtusángulo, circuncentro en el exterior del triángulo.
- Triángulo acutángulo, circuncentro en interior del triángulo.
Circunferencia circunscrita de cuadriláteros
Los cuadriláteros inscritos poseen propiedades particulares, incluyendo que los ángulos opuestos son suplementarios que se deduce a partir de la generalización del arco capaz.
La circunferencia circunscrita a un triángulo es la circunferencia que pasa por los tres vértices del triángulo. Esta circunferencia siempre existe si los vértices del triángulo no estén alineados, es decir, existe si el área del triángulo no es cero.
La circunferencia circunscrita a un cuadrilátero es la circunferencia que pasa por todos sus vértices. Esta circunferencia no siempre existe, por lo que, a los cuadriláteros que tienen una circunferencia circunscrita se les llama cuadriláteros cíclicos.
En general, la circunferencia circunscrita a un polígono, si existe, es la circunferencia que pasa por todos su vértices.
Al centro de la circunferencia circunscrita se le llama circuncentro. En el caso del triángulo, a este punto se le refiere como el circuncentro del triángulo.

No hay comentarios:
Publicar un comentario