Geometría - Triángulos

La circunferencia exinscrita a un triángulo, la cual es tangente a uno de los lados de un triángulo y a sendas prolongaciones de los otros dos. Al centro de la circunferencia exinscrita se le llama exincentro. Se pueden trazar tres circunferencias exinscritas para cada triángulo.

Propiedades

• Una circunferencia exinscrita está en el exterior de un triángulo, excepto el punto de tangencia que pertenece , exactamente. a uno de los lados del triángulo.

• Las bisectrices exteriores e interiores son normales entre sí.
• A las circunferencias exinscritas y la circunferencia inscrita se les llama circunferencias tritangentes al triángulo.

Radios

A continuación el valor del radio de cada circunferencia exinscrita:

• 

• 

•  ²

Exincentro

El exincentro es el centro de una circunferencia exinscrita; es la intersección de las bisectrices de cualesquiera dos de los tres ángulos exteriores y la bisectriz interior del ángulo opuesto del lado tangente de un triángulo. ³ Todo triángulo posee tres exincentros, uno en el trapecio infinito exterior de cada lado..

La circunferencia inscrita y las tres circunferencias exinscritas trazadas a partir de los exincentros.

Desde él, se puede trazar una circunferencia que es tangente a un lado y la prolongación de los otros dos.

Como consecuencia de que la circunferencia es tangente a las prolongaciones de los lados, la distancia mayor desde el vértice a los puntos de tangencia son iguales y sumadas equivalen al perímetro del triángulo.

Características

• El exincentro siempre está fuera del triángulo.
• El exincentro es centro de la circunferencia exinscrita.
• También pasa por el exincentro la bisectriz interior opuesta al lado al que es tangente la circunferencia exinscrita.

Circunferencias del triángulo y puntos notables

A lo largo de los siglos el interés de los matemáticos por el triángulo ha sido enorme, por lo que se conocen muchas de sus propiedades. Los geómetras de la grecia clásica lo estudiaron con tanta profundidad, que difícilmente se podría pensar en encontrar novedades sobre la figura geométrica más sencilla. Pero sin embargo se están descubriendo contantemente teoremas nuevos sobre el triángulo, aunque estos teoremas se complican tanto, que pierden elegancia y belleza, convirtiéndose en demasiado áridos y complejos como para ser estudiados en un curso elemental de geometría.
¿Es posible que algún teorema sencillo y elegante quede por encontrar y demostrar? No es fácil que sea así, pero no es imposible. Si te gusta investigar, aquí tienes un campo … es posible que descubras cosas ya descubiertas, pero eso no es nuevo: les ha pasado a muchos. Y tampoco hay que desengañarse. Ya llegará el momento en que descubras cosas nuevas, que antes nadie había pensado. Pero seguramente para eso ha de pasar un poco de tiempo.
Vamos a empezar por ver algunos resultados que habitualmente no se suelen ver en los libros sobre geometría plana elemental, pero que resultan ser muy elegantes:.

• Consideremos un triángulo ABC cualquiera, de manera que sobre cada uno de sus lados construimos un triángulo equilátero. Entonces al unir los centros (el baricentro) de los tres nuevos triángulos se forma un cuarto triángulo equilátero. Observa que da igual la foma de construir cada uno de los triángulos equiláteros: hacia adentro o hacia afuera, siempre que todos se construyan todos hacia adentro o todos hacia afuera). Este teorema ha sido atribuido a Napoleón. No conozco ninguna demostración, y no sé por tanto si es fácil o difícil.

Uniendo los centros con triángulos hacia afuera

Uniendo los centros con triángulos hacia adentro

Uniendo los centros con dos triángulos hacia afuera y uno hacia adentro

Pero además sigue siendo válido incluso cuando el triángulo degenera en un segmento, tal y como se observa en la siguiente figura:

• El siguiente teorema se demostró en 1821, y es llamado “de los 9 puntos”. Dice lo siguiente: “Dado un triángulo cualquiera ABC, situemos sobre él las siguientes ternas de puntos:
  • Los puntos medios de los tres lados a, b y c, que llamamos a_m , b_m, c_m (en la figura son los puntos negros)
  • Los pies de las tres alturas que llamamos p, q y r (en la figura los puntos rojos)
  • Los puntos medios de los segmentos que unen cada vértice con el ortocentro, que llamanos x, y z (en la figura los puntos amarillos).
  Entonces estos 9 puntos están sobre una circunferencia (en la figura en negro) que resulta tener un radio igual a la mitad de la circunferencia circunscrita al triángulo (en la figura en amarillo).

Martin Gardner
Circo matemático

Los teoremas que aparecen a continuación son clásicos, conocidos desde hace miles de años, pero no por ello resultan menos elegantes. Veamos primero algunas definiciones fundamentales sobre el triángulo.

• El circuncentro (O) es el centro de la circunferencia circunscrita a un triángulo. Es decir, es el centro de la circunferencia que pasa por los tres vértices. Dicho punto es el cruce de la tres mediatrices a los tres lados del triángulo. Demostrar esto no es difícil (clic aqui)
• El incentro (I) es el centro de la circunferencia inscrita al triángulo. Es decir, es el centro de la circunferencia tangente a los tres lados. Las tres bisectrices interiores se cortan en el incentro. Tampoco es difícil demostrar esto (clic aqui)
• El ortocentro (H) es el punto de corte de las tres alturas (clic aqui)
• El baricentro (G) es el centro centro de gravedad del triángulo y se obtiene mediante el corte de sus tres medianas (segmento que une un vértice con el punto medio del lado opuesto). Si quisieras que un triángulo de papel se sujete sobre la punta de un lápiz habrás de ponerlo sobre su baricentro (eso sí, cuando lo pongas, hazlo con mucho cuidado para que no se desequilibre). (clic aqui). El baricentro tiene una propiedad muy curiosa: está sobre la mediana, a un tercio del vértice y a dos tercios del lado. Aquí tienes una demostración, en dos pasos (clic aquí)
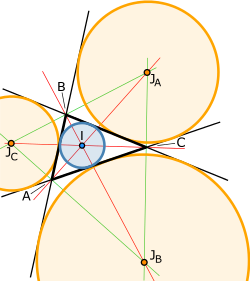
• Las circunferencias tangentes a los tres lados y a sus correspondientes prolongaciones reciben el nombre de exinscritas. Llamaremos r_a, r_b y r_c a los radios de las tres circunferencias exinscritas al triángulo ABC, de lados a, b y c. En la siguiente figura tienes las tres circunferencias exinscritas, la circunscrita y la inscrita.

Puedes ver cómo se obtiene el centro y radio de una de las circunferencias exinscritas de un triángulo aquí. (clic)

• Se cumple que O, G y H están alineados. La recta que los contiene se llama recta de Euler (clic) , y se verifica que

• El círculo de Euler es tal que su centro es el punto medio de OH y es tangente a las tres circunferencias exinscritas y a la circunferencia inscrita.
• Si R es el radio de la circunferencia circunscrita y r el de la inscrita se cumple que 4R = r_a + r_b + r_c - r
• Si p es el semiperímetro y S la superficie se cumple que S = pr = (p - a)r_a = (p - b)r_b = (p - c)r_c = 

No conozco las demostraciones de estas afirmaciones. Puede ser interesante buscarlas y entenderlas. Cuentas con la ventaja de que no son complicadas de entender. Así que anímate.

Te hago una propuesta para que investigues ¿Nunca te has parado a pensar porqué los tres ángulos de un triángulo tienen que sumar 180º?. ¿Porqué no son 160º por ejemplo?: ¿Es muy difícil demostralo?. ¿En qué axioma hay que apoyarse? ¿Qué sabes del axioma de Euclides? ¿Sabes algo de las geometrías no euclidianas? Aquí aparece un capítulo importante de las Matemáticas del cual vale la pena conocer algo.