Teorema de Menelao

Triángulo ABC cortado por la recta EDF.

El teorema de Menelao, atribuido a Menelao de Alejandría, es un teorema acerca de triángulos en geometría plana.

Teniendo en cuenta los puntos A, B, C que forman el triángulo ABC, y los puntos D, E, F que se encuentran en las líneas de BC, AC, AB, entonces el teorema establece que D, E, F son colineales si y sólo si:

\frac {EA}{EC} \cdot \frac {DC}{DB} \cdot \frac {FB}{FA} = 1

En cambio, si se utilizan segmentos dirigidos, será:¹

\frac {AE}{EC} \cdot \frac {CD}{DB} \cdot \frac {BF}{FA} = -1

Teorema de Menelao:

Los puntos X, Y, Z situados en los lados BC, CA y AB de un triángulo (o en sus prolongaciones) están alineados si y solamente si:

El Teorema de Steiner–Lehmus, es un teorema de geometría elemental, formulado porC. L. Lehmus y probado posteriormente por Jakob Steiner.

Todo triángulo que tenga dos bisectrices iguales, es un triángulo isósceles.

El teorema fue por primera vez mencionado en 1840 en una carta escrita por C. L. Lehmus enviada para C. Sturm, en la cual pidió una prueba puramente geométrica a C. Sturm, el cual pasó la petición a otros matemáticos y Jakob Steiner fue uno de los primeros en ofrecer una solución. El teorema se convirtió en un tema bastante popular en la geometría elemental desde entonces con una publicación un tanto regular de artículos sobre el mismo.

|AE|=|BD|,\,\alpha=\beta,\, \gamma=\delta

\Rightarrow \triangle ABC \text{ es isosceles}

teorema del coseno, denominado también como ley de cosenos ¹ , es una generalización del teorema de Pitágoras en los triángulos rectángulos que se utiliza, normalmente, en trigonometría.

El teorema relaciona un lado de un triángulo cualquiera con los otros dos y con el coseno del ángulo formado por estos dos lados:

Teorema del coseno
Dado un triángulo ABC cualquiera, siendo α, β, γ, los ángulos, y a, b, c, los lados respectivamente opuestos a estos ángulos entonces:

$c^2 = a^2 + b^2 - 2ab\cos\gamma\,$

En la mayoría de los idiomas, este teorema es conocido con el nombre de teorema del coseno, denominación no obstante relativamente tardía. En francés, sin embargo, lleva el nombre del matemático persa Ghiyath al-Kashi que unificó los resultados de sus predecesores.

Historia

Los Elementos de Euclides, que datan del siglo III a. C., contienen ya una aproximación geométrica de la generalización del teorema de Pitágoras: las proposiciones 12 y 13 del libro II, tratan separadamente el caso de un triángulo obtusángulo y el de un triángulo acutángulo. La formulación de la época es arcaica ya que la ausencia defunciones trigonométricas y del álgebra obligó a razonar en términos de diferencias de áreas.³ Por eso, la proposición 12 utiliza estos términos:

«En los triángulos obtusángulos, el cuadrado del lado opuesto al ángulo obtuso es mayor que los cuadrados de los lados que comprenden el ángulo obtuso en dos veces el rectángulo comprendido por un lado de los del ángulo obtuso sobre el que cae la perpendicular y la recta exterior cortada por la perpendicular, hasta el ángulo obtuso».

Euclides, Elementos.⁴

Siendo ABC el triángulo, cuyo ángulo obtuso está en C, y BH la altura respecto del vértice B (cf. Fig. 2 contigua), la notación moderna permite formular el enunciado así:

Fig. 2 - Triángulo ABC con alturaBH.

$AB^2 = CA^2 + CB^2 + 2\ CA\ CH$

Faltaba esperar la trigonometría árabe-musulmana de la Edad Media para ver al teorema evolucionar a su forma y en su alcance: el astrónomo y matemático al-Battani⁵ generalizó el resultado de Euclides en la geometría esférica a principios del siglo X, lo que permitió efectuar los cálculos de la distancia angular entre el Sol y la Tierra.⁶ ⁷ Fue durante el mismo período cuando se establecieron las primeras tablas trigonométricas, para las funciones seno y coseno. Eso permitió a Ghiyath al-Kashi,⁸matemático de la escuela de Samarcanda, de poner el teorema bajo una forma utilizable para la triangulación durante el siglo XV. La propiedad fue popularizada en occidente por François Viète quien, al parecer, lo redescubrió independientemente.⁹

Fue a finales del siglo XVII cuando la notación algebraica moderna, aunada a la notación moderna de las funciones trigonométricas introducida por Euler en su libroIntroductio in analysin infinitorum, permitieron escribir el teorema bajo su forma actual, extendiéndose el nombre de teorema (o ley) del coseno.¹⁰

El teorema y sus aplicaciones

El teorema del coseno es también conocido por el nombre de teorema de Pitágoras generalizado, ya que el teorema de Pitágoras es un caso particular: cuando el ángulo

\gamma \,

es recto o, dicho de otro modo, cuando

\cos\gamma = 0 \,

, el teorema del coseno se reduce a:

$\,c^2=a^2+b^2$

que es precisamente la formulación del teorema de Pitágoras.

Fig. 3 - Utilización del teorema del coseno: ángulo o lado desconocido.

El teorema se utiliza en triangulación (ver Fig. 3) para resolver un triángulo, y saber determinar:

el tercer lado de un triángulo cuando conocemos un ángulo y los lados adyacentes:

$c = \sqrt{a^2+b^2-2ab\cos\gamma}$ .

los ángulos de un triángulo cuando conocemos los tres lados:

$\gamma = \arccos \frac{a^2+b^2-c^2}{2ab}$ .

Estas fórmulas son difíciles de aplicar en el caso de mediciones de triángulos muy agudos utilizando métodos simples, es decir, cuando el lado c es muy pequeño respecto los lados a y b —o su equivalente, cuando el ángulo γ es muy pequeño.

Existe un corolario del teorema del coseno para el caso de dos triángulos semejantes ABC y A'B'C'

$\,cc' = aa' + bb' - (ab'+a' b)\cos\gamma$ .

Demostraciones

Por desglose de áreas

Fig. 4a - Demostración del teorema del coseno por desglose de áreas, cuando el ángulo es agudo.

Un cierto número de las demostraciones del teorema hacen intervenir un cálculo de áreas. Conviene en efecto remarcar que

a², b², c² son las áreas de los cuadrados de lados respectivos a, b, c.
ab cos(γ) es el área de un paralelogramo de lados a y b que forman un ángulo de 90°-γ (para una prueba, ver elapéndice).

Dado que cos(γ) cambia de signo dependiendo de si γ es mayor o menor a 90°, se hace necesario dividir la prueba en dos casos.

La figura 4a (contigua) divide un heptágono de dos maneras diferentes para demostrar el teorema del coseno en el caso de un ángulo agudo. La división es la siguiente:

En verde, las áreas a², b² la izquierda, y el área , c² a la derecha.
En rojo, el triángulo ABC en ambos diagramas y en amarillo triángulos congruentes al ABC.
En azul, paralelogramos de lados a y b con ángulo 90°-γ.

Igualando las áreas y cancelando las figuras iguales se obtiene que

{\textstyle a^2+b^2 = c^2+2ab\, \cos\gamma}

, equivalente al Teorema del coseno.

Fig. 4b - Demostración del teorema del coseno por desglose de áreas, cuando el ángulo es obtuso.

La figura 4b (contigua) desglosa un hexágono de dos maneras diferentes para demostrar el teorema del coseno en el caso de un ángulo obtuso. La figura muestra

En verde a², b² la izquierda y c² a la derecha.
En azul -2ab cos(γ), recordando que al ser cos(γ) negativo, la expresión completa es positiva.
En rojo, dos veces el triángulo ABC para ambos lados de la figura.

Igualando áreas y cancelando las zonas rojas da

\,a^2+b^2-2ab\cos\gamma = c^2

, como queríamos demostrar.

Por el teorema de Pitágoras

Notemos que el Teorema de Cosenos es equivalente al Teorema de Pitágoras cuando el ángulo

\gamma

es recto. Por tanto sólo es necesario considerar los casos cuando c es adyacente a dos ángulos agudos y cuando c es adyacente a un ángulo agudo y un obtuso.

Primer caso: c es adyacente a dos ángulos agudos.

Caso 1: c es adyacente a dos ángulos agudos

Consideremos la figura adjunta. Por el teorema de Pitágoras, la longitud c es calculada así:

(left) $c^2 = h^2 + u^2\,$

Pero, la longitud h también se calcula así:

(left) $h^2 = a^2 - (b-u)^2\,$

Sumando ambas ecuaciones y luego simplificando obtenemos:

$c^2 = a^2 - b^2 + 2bu\,$

Por la definición de coseno, se tiene:

$cos\gamma\,= \frac{b-u}{a}$

y por lo tanto:

$u = b- a \,\cos\gamma\,$

Sustituimos el valor de u en la ecuación para c², concluyendo que:

$c^2 = a^2 +b^2 -2ab\, \cos \gamma$

con lo que concluye la prueba del primer caso.

Segundo caso: c es adyacente a un ángulo obtuso.

Caso 2: c es adyacente a un ángulo obtuso

Consideremos la figura adjunta. El teorema de Pitágoras establece nuevamente

c^2 = h^2 + u^2

pero en este caso

h^2 = a^2 - (b+u)^2

. Combinando ambas ecuaciones obtenemos

c^2 = u^2 + a^2 - b^2 - 2bu - u^2

y de este modo:

$c^2 = a^2 -b^2 -2bu\,$ .

De la definición de coseno, se tiene

cos\gamma\,= \frac{b+u}{a}

y por tanto:

$u = a\, \cos\gamma -b\,$ .

Sustituimos en la expresión para

c^2 = a^2 - b^2 - 2b (a \cos\gamma\ - b)

, concluyendo nuevamente

$c^2 = a^2 +b^2 -2ab\, \cos \gamma\,$ .

Esto concluye la demostración. c² = a² - b² - 2b(a cos(γ) - b) Es importante notar, que si se considera a u como un segmento dirigido, entonces sólo hay un caso y las dos demostraciones se convierten en la misma.

Por la potencia de un punto con respecto a un círculo

Fig. 6 - Demostración del teorema del coseno utilizando la potencia de un punto con respecto a un círculo.

Consideremos un círculo con centro en B y radio BC, como en la figura 6. Si AC es tangente al círculo, nuevamente se tiene el Teorema de Pitágoras. Cuando AC no es tangente, existe otro punto K de corte con el círculo. LA potencia del punto A con respecto a dicho círculo es

$AP\cdot AL=AC\cdot AK= AC (AC+CK)$ .

Por otro lado, AL = c+a y AP = c-a de modo que

$AP\cdot AL = (c+a)(c-a) = c^2 -a^2$ .

Además, CK= -2a cos(γ) (ver el apéndice) por lo que

$AC(AC+CK) = b(b -2a\,cos(\gamma))$ .

Igualando las expresiones obtenidas se llega finalmente a:

$c^2=a^2+b^2-2a\;b\,\cos(\gamma)$

Contrariamente a las precedentes, para esta demostración, no es necesario recurrir a un estudio por caso pues las relaciones algebraicas son las mismas para el caso del ángulo agudo.

Por el cálculo vectorial

Utilizando el cálculo vectorial, más precisamente el producto escalar, es posible encontrar el teorema del coseno en algunas líneas:

$c^2\,$	$=\lVert\overrightarrow{\mathrm{AB}}\lVert^2$
	$= \lVert\overrightarrow{\mathrm{CB}}-\overrightarrow{\mathrm{CA}}\lVert^2$
	$=\lVert\overrightarrow{\mathrm{CB}}\lVert^2-2\cdot\overrightarrow{\mathrm{CB}}\cdot\overrightarrow{\mathrm{CA}}+\lVert\overrightarrow{\mathrm{CA}}\lVert^2$
	$=\mathrm{CB}^2-2\cdot\left\|\mathrm{CB}\right\|\cdot\left\|\mathrm{CA}\right\|\cos\widehat{\mathrm{ACB}}+\mathrm{CA}^2$
	$=a^2+b^2-2ab \cos\gamma\,$

Demostración geométrica

Cualquiera que sea el triángulo ABC se cumple que

AB^2=AC^2+BC^2-2 \cdot AC\cdot BC\cdot \cos \gamma.

Si el ángulo γ es igual a 90º, la proposición se colige del Teorema de Pitágoras, puesto que cos 90º=0. En el caso de que el ángulo sea agudo, según un teorema anterior se tiene que

AB^2=AC^2+BC^2-2 \cdot BC \cdot CD.

En el triángulo ACD, se cumple que

CD= AC \cos \gamma.

. Por ello

AB^2=AC^2+BC^2-2\cdot BC \cdot AC \cdot \cos \gamma.

Sea esta vez γ un ángulo obtuso, según un teorema pertimente, se cumple que

AB^2=AC^2+BC^2+2\cdot BC \cdot CD,

pero en el triángulo ADC ¹¹ , se halla que

CD= AC \cdot \cos(\widehat{ACD}).

. Sin embargo el ángulo ACD es el suplemento del ángulo γ del triángulo ABC. De esta manera se tiene que

\cos(\widehat{ACD})=-\cos \gamma

, por consiguiente

-AC \cos \gamma

y finalmente

AB^2=AC^2+BC^2-2 \cdot AC \cdot BC \cdot \cos \gamma,

quedando demostrado el teorema.¹²

Generalización en geometrías no euclídeas

Fig. 7 - Triángulo esférico: dimensiones reducidas z, b y c ; ángulos α, β y γ.

Para una superficie no euclídea de curvatura K, señalamos con R el radio de curvatura. Este verifica

\,R = 1/\sqrt{|K|}

Definimos entonces las dimensiones reducidas del triángulo:

\,a = BC/R

\,b = AC/R

\,c = AB/R

En el caso de un triángulo esférico, a, b y c corresponden a la medida angular de los segmentos de circunferencia maximal¹³ [BC], [AC] y [AB] (ver Fig. 7).

Geometría esférica

Cuando el radio de curvatura es muy grande comparado con las dimensiones del triángulo, es decir cuando

\,a <\!\!< 1

esta expresión se simplifica para dar la versión euclídea del teorema del coseno. Para hacerlo,

\,\cos a = 1 - a^2/2 + O(a^3)

, etc.

Existe una identidad similar que relaciona los tres ángulos:

\cos\gamma = \cos\alpha\,\cos\beta + \sin\alpha\,\sin\beta\,\cos c

Geometría hiperbólica

En un triángulo hiperbólico ABC, el teorema del coseno se escribe

\cosh c = \cosh a\,\cosh b - \sinh a\,\sinh b\,\cos\gamma

Cuando el radio de curvatura se vuelve muy grande frente las dimensiones del triángulo, encontramos el teorema del coseno euclídeo a partir de los desarrollos limitados

\,\sinh a = a + O(a^3)

, etc.,

\,\cosh a = 1 + a^2/2 + O(a^3)

, etc.

Generalización en el espacio euclídeo

Fig. 8 - Tetraedro: vértices, caras y ángulos.

Consideremos un tetraedro A₁A₂A₃A₄ del espacio euclídeo, siendo:

\,\mathrm S_k

la cara opuesta al vértice

\mathrm A_k\

;

\,s_k

la superficie de

\mathrm S_k\

;

\,\Delta_k

el plano que contiene a la cara

\mathrm S_k\

;

\,\theta_{ij}

el ángulo diedral

\widehat{(\Delta_i, \Delta_j)}

(La figura 8, contigua, presenta la notación de los vértices, caras y ángulos del tetraedro).

Entonces, las superficies y ángulos verifican:

\,s_4^2 = s_1^2+s_2^2+s_3^2 - 2s_1s_2\cos\theta_{12}\,

- 2s_1s_3\cos\theta_{13} - 2s_2s_3\cos\theta_{23}\,

Apéndice

Área de un paralelogramo

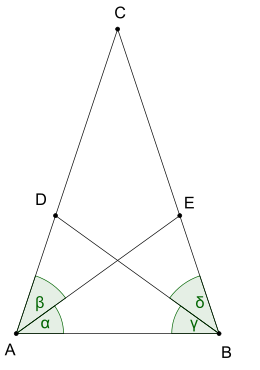
Deducción del teorema sobre área de un paralelogramo.

Se afirma:

Un paralelogramo cuyos lados miden a y b, formando un ángulo de 90°-γ, tiene un área de abcos(γ).

Considérese un paralelogramo de lados a y b, formando un ángulo de θ, como en el diagrama. Dividiendo el paralelogramo por medio de una diagonal arroja dos zonas triangulares. En una de ellas, se construye una altura h como se muestra en la figura.

La zona triangular roja tiene por área ah/2. Por definición, sin(θ)=h/b,¹⁴ de modo que h=b sin(θ). La sustitución en la fórmula del área triangular prueba que:¹⁵

El área de un triángulo en donde dos lados de medidas a y b forman un ángulo de θ es

$A_T=\frac{ab\, \sin\theta}{2}$

Dado que el área del paralelogramo es el doble del triángulo,¹⁶ se concluye que

El área de un paralelogramo de lados a y b formando un ángulo de θ es

$A_P=ab\, \sin\theta$

La conclusión se sigue notando que si θ=90-γ entonces sen(θ)=sen(90°-γ) = cos(γ). Se hace notar también que la demostración es independiente de cual de las diagonales del paralelogramo se escoja, puesto que sen(θ)=sen(180°-θ).

Cuerdas en un círculo

Diagrama usado en la prueba basada en potencia de un punto.

En la demostración del Teorema del coseno usando potencia de un punto, se afirma que el segmento CK en el diagrama mide precisamente -2a cos(γ).

La demostración más sencilla consiste en prolongar el segmento CB hasta cortar nuevamente la circunferencia en un punto D, de modo que CD es un diámetro del círculo, puesto que pasa por el centro del mismo.

Al ser un diámetro, el ángulo inscrito CKD es necesariamente recto por lo que el triángulo CKD es rectángulo. El ángulo DCKmide θ=180°-γ y por definición:

$\cos(\theta) = \frac{CK}{CD} = \frac{CK}{2a}$

y por tanto

$CK = 2a \cos(\theta) = 2a\cos(180^\circ - \gamma) = -2a \cos(\gamma)$

ya que cos(180°-x) = -cos(x) para cualquier valor de x.

AMIGOS PARA SIEMPRE

Páginas

lunes, 22 de febrero de 2016

Geometría - Triángulos