teorema de los senos1 o también conocido como ley de los senos 2 es una relación de proporcionalidadentre las longitudes de los lados de un triángulo y los senos de sus respectivos ángulos opuestos.
Usualmente se presenta de la siguiente forma:
|
Demostración
A pesar de ser de los teoremas trigonométricos más usados y de tener una demostración particularmente simple, es poco común que se presente o discuta la misma en cursos de trigonometría, de modo que es poco conocida.
Dado el triángulo ABC, denotamos por O su circuncentro y dibujamos su circunferencia circunscrita. Prolongando el segmento BO hasta cortar la circunferencia, se obtiene un diámetro BP.
Ahora, el triángulo PCB es recto, puesto que BP es un diámetro, y además los ángulos A y P son congruentes, porque ambos son ángulos inscritos que abren el segmento BC (Véase definición de arco capaz). Por definición de la función trigonométrica seno, se tiene
donde R es el radio de la circunferencia. Despejando 2R obtenemos:
Repitiendo el procedimiento con un diámetro que pase por A y otro que pase por C, se llega a que las tres fracciones tienen el mismo valor 2R y por tanto son iguales.
La conclusión que se obtiene suele llamarse teorema de los senos generalizado y establece:
|
Puede enunciarse el teorema de una forma alternativa:
|
Aplicación
El teorema de los senos es utilizado para resolver problemas en los que se conocen dos ángulos del triángulo y un lado opuesto a uno de ellos. También se usa cuando conocemos dos lados del triángulo y un ángulo opuesto a uno de ellos.
Puede ser empleado la ley de los senos, con reajustes circunstanciales, en:
- cálculo de la altura de un árbol
- hallar el ángulo de elevación del suelo
- plano para construcción de puentes
- estudio y dibujo de carriles de una autopista
- itinerario de un planeo
- ubicación de un foco de incendio
- situación de un transmisor de radio clandestino
- la altitud de una montaña y otros casos. 3
Relación con el área del triángulo
Para un triángulo ABC, el área se calcula como ah/2 donde h es la medida de la altura sobre la base a. Nuevamente, por definición de seno, se tiene sen C = h/b o lo que es lo mismo h = b sen C, de modo que se cumple:
 .
.
Sin embargo, el teorema de los senos implica que c = 2R sen C, por lo que al substituir en la expresión anterior se obtiene un nuevo teorema:
En un triángulo cada lado es directamente proporcional al seno del ángulo opuesto.
Ejercicios
De un triángulo sabemos que: a = 6 m, B = 45° y C = 105°. Calcula los restantes elementos.
Calcular el radio del círculo circunscrito en un triángulo, donde A = 45°, B = 72° y a=20m.
teorema de Marden, llamado así por Morris Marden, da un relación geométrica entre los ceros de un polinomio de tercer grado con coeficientes complejos y los ceros de su derivada.
Un polinomio cúbico tiene tres ceros en el plano complejo, que en el caso más general forman un triángulo, el teorema de Gauss-Lucas afirma que las raíces de su derivada caen también en este triángulo. El teorma de Marden precisa más concretamente su posición:
Por el teorema de Gauss-Lucas, la raíz de la doble derivada de un polinomio p"(z) debe ser el promedio de los dos focos de la elipse, que es el punto central de la elipse y a su vez el centroide del triángulo.
En el caso especial de que el triángulo sea equilátero (tal como sucede, por ejemplo, para el polinomio p(z) = z3 − 1), la elipse inscrita degenera en un círculo, y la derivada de p tiene una raíz doble en el centro del círculo. Recíprocamente, si la derivada tiene una raíz doble, entonces el triángulo debe ser equilátero.1
Una versión más general del teorema, debida a Linfield (1920), es aplicable a polinomios p(z) = (z − a)i (z − b)j (z − c)k cuyos grados cumplan que i + j + k pueda ser mayor que tres, pero que sólo tenga tres raíces a, b y c. Para tales polinomios, las raíces de la derivada pueden ser raíces múltiples de un polinomio dado (las raíces cuyos exponentes son mayores a uno) y en los focos de una elipse cuyos puntos de tangencia al triángulo dividen a sus lados en los ratios i : j, j : k y k : i.
Otra generalización devida a Parish (2006) es para n-gonos: algunos n-gonos tienen admiten una elipse inscrita que sea tangente a cada lado en el punto medio. El teorema de Marden todavía es aplicable: los focos de esta elipse tangente en los puntos medios son ceros del polinomio derivado cuyos ceros son los vértices del n-gono.
Marden (1945, 1966) atribuye lo que se llama teorema de Marden a Siebeck (1864) y cita nueve artículos que incluían una versión del teorema. Dan Kalman ganó en 2009 el galardón Lester R. Ford de la Mathematical Association of America por su artículo de 2008 en el American Mathematical Monthly que describía el teorema. |


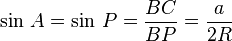



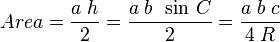 .
.
No hay comentarios:
Publicar un comentario