lunes, 22 de febrero de 2016

Geometría - Triángulos


la fórmula de Herón, atribuida invención al matemático griego, Herón de Alejandría,1 , da elárea de un triángulo conociendo las longitudes de sus tres lados a, b y c:
\acute{A}rea = \sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}
donde s es el semiperímetro del triángulo:
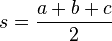s = \frac{a+b+c}{2}.
Cualquier polígono simple puede ser separado en triángulos que a lo más tienen un lado común o un vértice común, mediante diagonales que parten de un único vértice apropiado. Esta subdivisión y la aplicación de la norma herodiana para el área triangular, facilita el cálculo del área de la región plana encerrada por el polígono simple, con solo medir longitudes, allí radica su importancia.
La fórmula también puede expresarse de estas otras formas:
\acute{A}rea ={\ \sqrt{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)\ \over 16}\,}
\acute{A}rea ={\ \sqrt{2(a^2 b^2+a^2c^2+b^2c^2)-(a^4+b^4+c^4)\ \over 16}\,}
\acute{A}rea = {\ \sqrt{(a+b+c)(a+b-c)(b+c-a)(c+a-b)\,}\ \over 4}\,
\acute{A}rea = \frac{1}{4}\sqrt{(a^2 + b^2 + c^2)^2 - 2(a^4 + b^4 + c^4)}.
La fórmula de Herón se distingue de otras fórmulas para hallar el área de un triángulo, como la de la mitad de la base por la altura o la de la mitad del módulo de un producto cruz de dos lados, por no requerir ninguna elección arbitraria de un lado como base o un vértice como origen.

Triángulo de lados a, b, c.

Ejemplo

Un triángulo con lados 3, 25 y 26 (unidades de longitud) tiene semiperímetro (3 + 25 + 26)/2 = 27 (unidades de longitud). Así, su área es \acute{A}rea = \sqrt{27 \cdot 24 \cdot 2 \cdot 1}=36. (Unidades de Área).

Historia

El hallazgo de la fórmula se ha atribuido a Herón de Alejandría, y se puede encontrar una prueba en su libro, Métrica, escrito en el año 60 dC. Se ha presumido que el físico matemático griego, Arquímedes, haya conocido la fórmula, dos siglos antes; y que lo puesto en Métrica es una colección de los conocimientos matemáticos disponibles en el mundo antiguo, es posible que la norma areal preceda a la referencia que figura en el tratado heroniano.2
Sépase, una regla de área triangular equivalente a la de Herón:
\acute{A}rea=\frac1{2}\sqrt{a^2c^2-\left(\frac{a^2+c^2-b^2}{2}\right)^2}, donde a \ge b \ge c
fue conseguida por matemáticos chinos, independientemente de los griegos. Fue publicada en Shushu Jiuzhang ("Tratado matemático en nueve secciones"), escrito porQin Jiushao y publicado en el año 1247.

Demostración

Una demostración moderna, que emplea álgebra y trigonometría (bastante distinta a la que dio Herón en su libro Métrica), podría ser la siguiente:
Demostración

Prueba usando el teorema de Pitágoras

Triángulo con altitud h cortando con base c
La prueba original de Herón hace uso de los cuadriláteros cíclicos, mientras que otros argumentos apelan a latrigonometría como el anterior, o para el incentro y un excentro del triángulo [2]. El siguiente argumento reduce la fórmula de Herón directamente al teorema de Pitágoras utilizando únicamente medios elementales.
En la forma 4Á 2 = 4s(s − a)(s − b)(s − c), La parte izquierda de la fórmula de Herón se reduce a (ch)2, o bien
(cb)^2-(cd)^2 que es lo mismo que c^2(b^2-d^2)
usando b 2 − d 2 = h 2 por el teorema de Pitágoras; en cuanto a la parte derecha de la fórmula, puede expresarse como
\displaystyle (s(s-a)+(s-b)(s-c))^2 - (s(s-a)-(s-b)(s-c))^2
vía la identidad (p + q) 2 − (p − q) 2 = 4pq. Por tanto, basta mostrar
cb=s(s-a)+(s-b)(s-c), \,
y
cd = s(s-a)-(s-b)(s-c). \,
En lo que se refiere a la primera forma, expandiéndola se obtiene lo siguiente:
2s^2 - s(a + b + c) + cb. \,
y que se reduce a cb al sustituir 2s = (a + b + c) y simplificando.
Respecto la segunda expresión, s(s − a) − (s − b)(s − c), expandiéndola y sustituyendo el valor de s=(a+b+c)/2 se reduce hasta
(b^2 +c^2 - a^2)/2\,
Sustituyendo b 2 por d 2 + h 2 y a 2 por (c − d) 2 + h 2, por teorema de Pitágoras, entonces simplificando se obtiene cd según se requería.

Prueba por la Ley de los cosenos

Se parte del hecho de que para todo triángulo su área es igual a  A_{\Delta} = \frac{1}{2}bc sen A
elevando al cuadrado  A_{\Delta}^2 = \frac{1}{4}(bc)^2 sen^2 A
pasando a coseno, por 4 y entre da  A_{\Delta}^2 = \frac{1}{16} \times 4 \times (bc)^2 ( 1- cos ^2 A
acomodando el producto  A_{\Delta}^2 = \frac{1}{16}[4(bc)^2 - 4(bc)^2 cos ^2 A]
factorizando diferencia de cuadrados  A_{\Delta}^2 = \frac{1}{16} (2bc + 2bc cos A) (2bc - 2bc cos A) (*)
pero por la ley de cosenos  2bc cos A = b^2+c^2-a^2  que reemplazado en el paso anterior (*)
\frac{1}{16}[2bc + ( b^2+c^2-a^2)] [2bc - ( b^2+c^2-a^2) ]
agrupando apropiadamente \frac{1}{16} [(b+c)^2 -a^2] [a^2 - (b-c)^2 ]
desarrollando diferencia de cuadrados y dividiendo cada uno de los factores entre dos,  \frac{1}{2}(a+b+c)\frac{1}{2} (b+c-a)\frac{1}{2} (a+b-c)\frac{1}{2} (a-b+c)
en cada factor teniendo presente que a+b+c = 2s. resulta  s(s-a) (s-b) (s-c)
como el último producto es el área al cuadrado, resulta:  A_{\Delta} = \sqrt{s(s-a) (s-b) (s-c)} 3

Estabilidad numérica

La fórmula de Herón dada más arriba es numéricamente inestable para triángulos de ángulos muy pequeños (como ocurre frecuentemente en astronomía). Una alternativa numéricamente más estable4 5 implica reordenar las longitudes de los lados de modo que a ≥ b ≥ c, y luego realizar el computo de acuerdo con la siguiente forma reordenada, de la fórmula de Herón:
\acute{A}rea = \frac{1}{4}\sqrt{(a+(b+c)) (c-(a-b)) (c+(a-b)) (a+(b-c))}.
En la fórmula precedente los paréntesis son absolutamente necesarios para evitar la inestabilidad numérica en la evaluación.

Generalizaciones

Desigualdad triangular,\{a,b,c\}\in\mathbb{R^+} .
La fórmula de Herón es un caso particular de la fórmula de Brahmagupta para el cálculo del área de cuadriláteros inscritos en una circunferencia; y ambas son casos particulares de la fórmula de Bretschneider para calcular área de un cuadrilátero.
Expresando parte de la fórmula de Herón (sólo los términos internos a la raíz) de forma matricial dentro de un determinante (determinante de Cayley-Menger) en términos de cuadrados de distancias de los tres vértices dados (más precisamente, el valor absoluto del determinante), obtenemos:
ilustra su similitud con la fórmula de Tartaglia para el volumen de un simple de tres.
\acute{A}rea=\frac{1}{4} \sqrt{\left|{det \begin{bmatrix} 0 & a^2 & b^2 & 1 \\ a^2 & 0 & c^2 & 1 \\ b^2 & c^2 & 0 & 1 \\ 1 & 1 & 1 & 0 \end{bmatrix}}\right|}
Donde a, b y c son las longitudes de los lados del triángulo y A será el área del mismo. Hay que asegurarse que los datos a, b y c que se proveen al determinante cumplan con la desigualdad triangular (véase figura), de lo contrario no se trataría de un triángulo y en ese caso el determinante daría resultados positivos o cero pero erróneos. Por otra parte con datos que si cumplan con la desigualdad triangular el determinante da siempre resultados negativos (no necesariamente erróneos pero inapropiados dentro de una raíz) por lo cual es necesario tomar el valor absoluto del determinante que está dentro de la raíz, de lo contrario obtendríamos resultados complejos.
Así como un triángulo está determinado por las longitudes de sus tres lados, un tetraedro lo está por las longitudes de sus seis lados. Tartaglia halló la fórmula del volumen del tetraedro en función de las longitudes de sus lados. Los determinantes de Cayley-Menger generalizan esta fórmula a dimensiones por encima de tres.
David P. Robbins descubrió otra generalización de la fórmula de Herón de pentágonos y hexágonos inscritos en un círculo.6

Fórmula tipo Herón para el volumen de un tetraedro

Si U, V, W, u, v, w son las longitudes de las aristas del tetraedro (las primeras tres forman un triángulo, u opuesto a U, y así sucesivamente), entonces7
\text{volumen} = \frac{\sqrt {\,( - a + b + c + d)\,(a - b + c + d)\,(a + b - c + d)\,(a + b + c - d)}}{192\,u\,v\,w}
donde
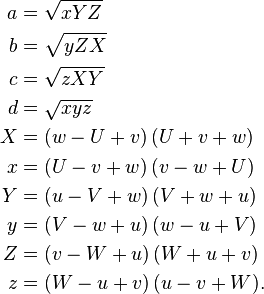
\begin{align} a & = \sqrt {xYZ} \\ b & = \sqrt {yZX} \\ c & = \sqrt {zXY} \\ d & = \sqrt {xyz} \\ X & = (w - U + v)\,(U + v + w) \\ x & = (U - v + w)\,(v - w + U) \\ Y & = (u - V + w)\,(V + w + u) \\ y & = (V - w + u)\,(w - u + V) \\ Z & = (v - W + u)\,(W + u + v) \\ z & = (W - u + v)\,(u - v + W). \end{align}




  No se tiene certeza de la época en que  vivió Herón de Alejandría, se supone que entre el siglo I a.C. y el s.II d.C.)
Herón se aleja de la formalización deductiva, característica de la matemática clásica griega, y es un genio eminentemente práctico. Su quehacer matemático es más próximo a la cultura egipcia o babilónica y hay quien cuestiona, incluso, su origen griego. Sí parece claro que es un seguidor de Arquímedes y lleva sus matemáticas a la ingeniería y agrimensura. No sólo hizo descubrimientos en geometría y en física, se le atribuye también la invención de una máquina de vapor. En física uno de sus teoremas más interesantes es el que demuestra que cuando la luz procedente de un objeto se refleja sobre espejos, la trayectoria   del rayo entre el objeto y el ojo es mínima. Este resultado parece una simple consecuencia del principio filosófico de Aristóteles de que la naturaleza procede siempre de la forma más sencilla o "económica".
Es más conocido en la historia de las matemáticas por la fórmula que lleva su nombre y nos permite calcular el área de un triángulo si conocemos sus tres lados:
Los lados son a, b y c. El semiperímetro es p.
Los traductores árabes dicen que esta fórmula ya la conocía Arquímedes. La demostración de Herón es del tipo geométrico usual  y aparece en uno de sus tratados, la  Métrica , que es encontrado en el año 1896. Ahora se puede obtener de una manera  trigonométrica. Si bien es cierto que en sus obras se encuentran algunas otras  demostraciones, la mayor parte de ellas se refieren a ejemplos numéricos de medida de longitudes, áreas y volúmenes, apreciándose grandes semejanzas entre sus resultados y los que conocemos de la antigua Mesopotamia.
Publicado por en

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)